基于BTT的反魚雷魚雷偏航角速率控制器設計

高 璇，周徐昌，潘 遜

?

基于BTT的反魚雷魚雷偏航角速率控制器設計

高 璇，周徐昌，潘 遜

(海軍工程大學 兵器工程系, 湖北 武漢, 430033)

反魚雷魚雷(ATT)的機動性對于其成功攔截來襲魚雷的概率有著重要作用, 而隨著ATT機動性的提高, 對其控制的難度也越來越大, 這就對ATT的控制器設計提出了更高的要求。可以選用傾斜轉彎(BTT)控制方式來提高ATT的機動性。研究了常規的比例-積分-微分(PID)控制, 智能PID控制, 預測函數控制(PFC)和模糊自適應PID控制, 并將它們分別應用于ATT的偏航角速率控制。仿真結果表明, 相對常規PID控制, 智能PID控制、PFC和模糊PID控制時, 系統控制過程平滑、無超調, 系統響應快速、穩定、準確, 且結果簡單, 實用性強。相比較而言, PFC相對智能PID控制和模糊PID控制響應速度更快, 而且計算量小, 更適應ATT偏航角速率控制系統的快速響應要求。

反魚雷魚雷; 傾斜轉彎; 機動性; 偏航角速率; 控制器

0 引言

傾斜轉彎(bank to turn, BTT)技術是飛機常用的控制方式, 現代導彈也采用了這種控制方式。在導彈截擊目標的過程中, 隨時繞其縱軸轉動, 使其所要求的法向過載矢量始終落在導彈對稱面上或者中間對稱軸上[1-3]。導彈在尋的過程中保持彈體相對縱軸穩定不動, 控制其在俯仰和偏航平面上產生相應的法向過載, 其總的法向力指向控制率所要求的方向上, 這種控制方式稱為側滑轉彎(skid to turn, STT)技術。

現代魚雷普遍采用STT控制方式, STT控制技術對于中近程、小機動的魚雷較為適宜, 但對超大機動魚雷和遠程攔截魚雷, 尤其是反魚雷魚雷(anti-torpedo torpedo, ATT)要求魚雷阻力小、機動過載大, STT方式則不適用。因此, 有必要采用更有效的控制策略, 以提高ATT的機動性, BTT控制技術可以作為ATT控制方式的一個選擇[4]。

BTT控制技術與STT控制技術的根本區別就在于, 在截擊目標的過程中, 采用STT控制方式的魚雷利用側滑轉彎實現對目標的跟蹤和導引, 而采用BTT控制方式的魚雷則利用傾斜轉彎實現。魚雷采用傾斜轉彎的BTT控制方式, 就是先使魚雷滾動一定的角度, 使其法向過載矢量與其中心對稱軸重合, 這樣魚雷可以獲得更大的轉彎力矩, 從而達到更小的轉彎半徑和更大的轉彎角速度, 以提高其機動能力[5-6]。

1 ATT的BTT模型

1.1 STT魚雷模型

魚雷的空間運動數學模型可由6個動力學方程和9個運動學方程描述, 在雷體坐標系下, 文獻[7]給出了魚雷空間運動方程的基本形式。方程組中包含了復雜的粘性力非線性項, 但是在魚雷的初始設計和研究階段, 不需要花費大量的人力物力去獲得粘性力的具體形式, 粘性力的線性項就可以滿足設計要求。因此, 為研究方便, 需作一定假設: 1) 魚雷為剛體, 其外形關于縱平面平面對稱; 在附加質量的計算中, 忽略不計魚雷外形可能存在的關于平面的不對稱性; 2) 魚雷完全浸沒在流體介質中, 并處于全沾濕狀態, 且流體介質為理想流體; 3) 坐標系為原點在魚雷浮心的雷體坐標系; 4) 流體動力位置力及阻尼力滿足線性條件; 5) 不考慮地球的自轉和地球的曲率, 近似認為地球坐標系為慣性坐標系; 6) 魚雷質量恒定, 且不計魚雷的慣性積。

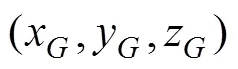
1.2 BTT魚雷模型

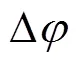
則位置力大小為

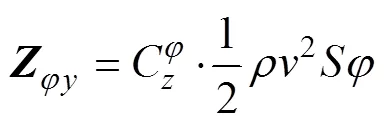
因此, 魚雷的側向空間運動方程組變為

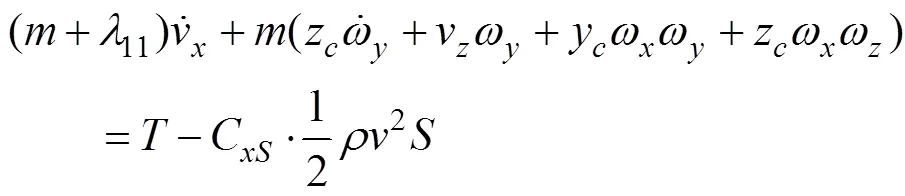
式(2)~式(5)為基于BTT的ATT側向運動動力學方程式, 與原STT模型運動學方程一起組成基于BTT的ATT側向運動數學模型。

2 ATT偏航角速率控制器

2.1 控制器設計

2.1.1 智能比例-積分-微分控制器

魚雷作為控制對象具有非線性和時變的特性, 采用定參數比例-積分-微分（proportion integration differentiation, PID)控制方法很難在魚雷追蹤目標過程中獲得很好的穩定性。因此, 智能PID控制器的設計思想是將參數K用時變的K()代替, 改善PID控制器的品質[8-11]。智能PID控制器的輸出應為

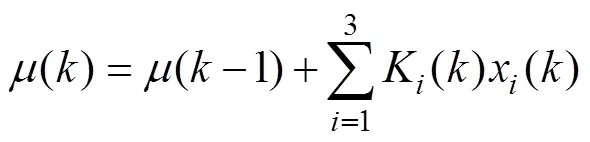
智能PID控制的關鍵是利用人工智能方法來設計時變的K()函數。為了提高控制系統的控制精度, 根據單神經元自適應PID控制器設計方法, 引入單神經元控制。單神經元的適應性是通過學習實現的, 學習方式可分為無監督學習和監督學習。無監督學習是在缺乏外界所提供的任何形式的反饋條件下所進行的學習。監督學習又稱有導師學習, 通過逐步調整權值減少實際輸出向量和預期輸出向量之間的差異。對于有監督的Hebb學習規則為

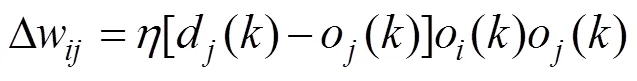
2.1.2 PFC控制器

預測函數控制(predictive functional control, PFC)在保持模型預測控制優點的同時, 通過引入基函數的概念, 增強了輸入控制量的規律性, 提高了快速性和準確性, 可有效地減少算法的在線計算量[12]。圖1所示為PFC控制基本原理框圖。

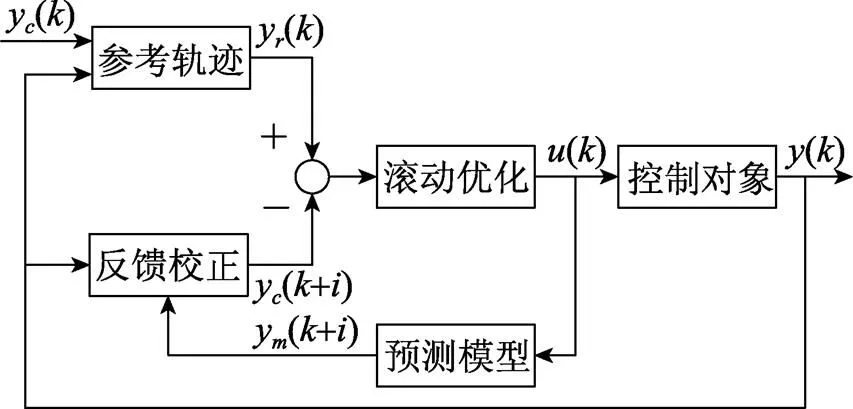
圖1 預測函數控制基本原理方框圖

PFC把控制輸入的結構視為確保控制系統性能的關鍵, 新加入的控制作用可表示為若干個已知從函數的線性組合, 即

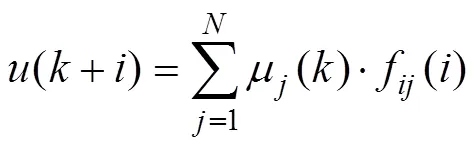
2.1.3 模糊PID控制器

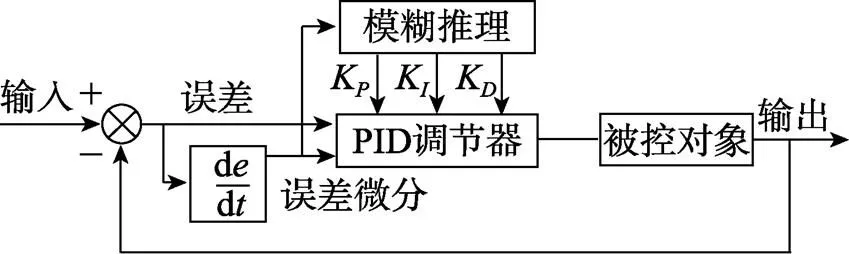
圖2 模糊自適應比例-積分-微分控制器結構

2.2 ATT偏航角速率控制系統

由某種導引率算出魚雷的法向加速度, 實際上等價于求出的是魚雷的偏航角速率, 這個角速率就是魚雷按照理論彈道航行所希望的偏航加速率。而對于魚雷的偏航控制系統來說, 這個偏航角速率也就是魚雷所希望的參考輸入。該角速率也確定了魚雷的偏航舵角, 以此來控制魚雷, 使其實際的偏航角速率趨于這個參考輸入。所以, 不管采用何種方式對魚雷進行導引, 魚雷水平面內的控制就是偏航角速率的控制。ATT在水平面內的機動也是由其偏航角速率控制系統實現的, 在基于BTT的ATT側向運動數學模型基礎上建立的ATT偏航角速率控制系統的SIMULINK模型如圖3所示。

圖3 反魚雷魚雷偏航角速率控制系統SIMULINK模型

2.3 控制系統仿真

設魚雷的偏航角速率回路的開環傳遞函數為

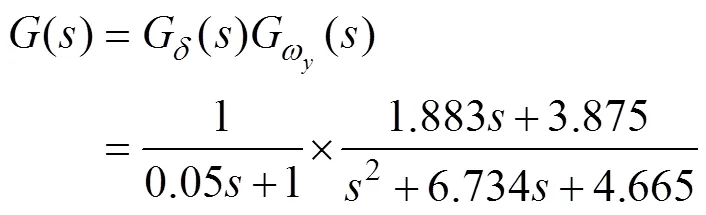
系統是一個穩定的零型系統, 對于階躍輸入存在較大的穩態誤差, 首先采用常規PID控制方法對其進行控制。

根據控制系統的性能指標, 可求出PID控制器的參數

3 結束語

由仿真結果可知, 在偏航角速率控制器設計中, 常規的PID控制系統存在著振蕩、超調。和常規PID控制相比, 采用智能PID控制、PFC控制和模糊PID控制時, 系統控制過程平滑、無超調, 系統響應快速、穩定、準確, 且結果簡單, 實用性強。相比較而言, PFC控制相對智能PID控制和模糊PID控制響應速度更快, 且計算量小, 能適應ATT偏航角速率控制系統的快速響應要求。

[1] 劉興堂. 導彈制導控制系統分析、設計與仿真[M]. 西安: 西北工業大學出版社, 2006: 33-135.

[2] 張靖南, 趙興鋒, 鄭志強. BTT導彈的發展現狀與趨勢[J]. 飛航導彈, 2006, 36(10): 37-43.

[3] 孟秀云. 導彈制導與控制系統原理[M]. 北京: 北京理工大學出版社, 2003.

[4] 高璇, 周徐昌, 潘遜. 基于BTT的反魚雷魚雷控制技術[J]. 兵工自動化, 2010, 29(10): 79-81. Gao Xuan, Zhou Xu-chang, Pan Xun. Control Technologies of Anti-Torpedo Torpedo Based on BTT[J]. Ordnance Industry Automation, 2010, 29(10): 79-81.

[5] 高璇, 周徐昌, 沈建森, 等. 基于BTT的反魚雷魚雷橫向-橫滾操縱性研究[J]. 艦船科學技術, 2011, 33(5): 94-97. Gao Xuan, Zhou Xu-chang, Shen Jian-sen, et al. Research on Roll Maneuverability of ATT Based on BTT[J]. Ship Science and Technology, 2011, 33(5): 94-97.

[6] Gao X, Zhou X C, Pan X. Roll Stability of ATT Based on BTT[C]//2011 3rd International Workshop on Intelligent System and Applications. 2011(1): 98-101.

[7] 嚴衛生. 魚雷航行力學[M]. 西安: 西北工業大學出版社, 2005.

[8] 邱道尹, 張健, 謝俊明, 等. 基于單神經元的自適應PID控制系統設計及仿真[J]. 華北水利水電學院學報, 2011, 32(1): 58-60. Qiu Dao-yin, Zhang Jian, Xie Jun-ming, et al. Design and Simulation of Self-adaptive PID Control System Based on Single Neuron[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2011, 32(1): 58-60.

[9] 陶永華. 新型PID控制及其應用[M]. 北京: 機械工業出版社, 2003.

[10] 劉金琨. 先進PID控制MATLAB仿真[M]. 北京: 電子工業出版社, 2004.

[11] 王亦平, 杜一平, 劉影, 等. 基于智能PID的魚雷控制算法探討[J]. 魚雷技術, 2005, 13(4): 26-28. Wang Yi-ping, Du Yi-ping, Liu Ying, et al. A Torpedo Control Algorithm Based on Intelligent Proportional Integrative Derivative[J]. Torpedo Technoloty, 2005, 13(4): 26-28.

[12] 劉超, 夏英華, 何海斌, 等. 基于模糊神經網絡的非線性系統預測函數控制研究[J]. 黑龍江工程學院學報, 2010, 24(3): 53-57. Liu Chao, Xia Ying-hua, He Hai-bin, et al. Research on Predictive Function Control of Nonlinear System Based on Fuzzy Neural Network[J]. Journal of Heilongjiang Institute of Technology, 2010, 24(3): 53-57.

[13] 吳艷敏, 關英姿, 王福生, 等. 基于模糊自適應PID的轉臺位置控制系統設計[J]. 現代電子技術, 2008, 32(19): 102-104. Wu Yan-min, Guan Ying-zi, Wang Fu-sheng, et al. Design on Position Control in the Turntable System Based on Fuzzy Self-adaptive PID[J]. Modern Electronics Technique, 2008, 32(19): 102-104.

Design of Yaw Angular Velocity Controller for Anti-Torpedo Torpedo Based on Bank-to-Turn

GAO Xuan， ZHOU Xu-chang, PAN Xun

(Department of weaponry Engineering, Naval University of Engineering, Wuhan 430033, China )

To enhance maneuverability of anti-torpedo torpedo(ATT), a new yaw angular velocity controller for ATT is designed by analyzing and adopting conventional PID control, intelligent PID control, predictive functional control(PFC), and fuzzy adaptive PID control, respectively based on bank-to-turn(BTT) control mode. Simulation results show that, compared with conventional PID control, intelligent PID control, PFC and fuzzy adaptive PID control make system control process smoother, faster and more accurate without overshoot. Particularly, PFC is more suitable for yaw angular velocity control of ATT because of its fastest response and least calculation.

anti-torpedo torpedo(ATT); bank-to-turn(BTT); maneuverability; yaw angular velocity; controller

TJ630.33

A

1673-1948(2012)05-0359-04

2012-02-28;

2012-04-26.

高 璇(1980-), 男, 博士, 主要研究方向為制導與控制技術.

(責任編輯: 楊力軍)