聯合對角化技術在空間譜估計中的應用

趙龍龍, 宋海巖

?

聯合對角化技術在空間譜估計中的應用

趙龍龍1, 宋海巖2

(1. 中國人民解放軍91388部隊, 廣東 湛江, 524022; 2. 黑龍江工程學院 電氣與信息工程學院, 黑龍江 哈爾濱, 150050)

在實際工程應用中, 傳統空間譜估計方法受噪聲、干擾及采樣效應等因素影響, 其性能明顯退化。為了克服這些因素對方位估計結果的影響, 提高算法性能, 本文將空時相關矩陣組代替傳統的采樣協方差矩陣, 利用聯合對角化這一新的數學工具, 研究了一種基于Jacobi旋轉正交聯合對角化的空間譜估計方法。通過對空時相關矩陣組進行聯合對角化, 得到了聯合對角化矩陣和對角化后的矩陣組, 最終利用聯合特征值和特征向量得到修正的陣列協方差矩陣, 并對空間譜估計處理器進行修正。仿真結果表明, 在不同的信噪比、快拍數等條件下, 基于聯合對角化的空間譜估計算法較傳統方法具有更高的分辨力和更低的均方根誤差, 能有效降低方位估計的信噪比門限, 進而改善傳統空間譜估計方法的方位估計性能。

空間譜; 聯合對角化; Jacobi旋轉; 空時相關矩陣組; 方位估計

0 引言

隨著電子信息科學的迅猛發展, 空間譜估計技術作為信號處理的一個重要分支, 在國民經濟及國防建設中發揮了重要作用, 并廣泛應用于聲納、雷達、醫學等研究領域, 引起了廣大研究者的高度重視[1]。最早, Burg將熵的概念推廣到空間譜估計領域, 由于該算法突破了瑞利限的限制, 吸引了廣大研究者對現代譜分析參數模型法進行廣泛研究[2]。其后, Capon提出了最小方差法(standard capon beamforming, SCB), 該方法可在保持來波方向信號能量不變的前提下, 使波束內其他方向的能量最小化, 同時獲得較高的分辨力以及較強噪聲干擾抑制能力[3]。20世紀80年代后期, Schmidt等人提出了多重信號分類(multiple signal classification, MUSIC)算法[4], 引起人們對子空間類算法的廣泛興趣, 促進了子空間類算法的興起, 開啟了高分辨空間譜估計技術的新紀元。20世紀90年代以來, 高分辨陣列處理與優化理論、信息論等相關學科密切結合, 出現了很多新的算法和理論。主要包括波束域高分辨陣列信號處理[5-6]、寬帶信號空間譜估計[7-8]、循環平穩信號的空間譜估計[9-10]以及基于高階累積量的空間譜估計[11-12]等。

然而, 在實際工程應用中, 高分辨空間譜估計方法的性能在很大程度上受信噪比、采樣效應等因素的影響。如何克服或消除這些因素的影響, 是制約高分辨算法走向工程實用化的關鍵。

針對這一問題, 本文從基陣接收信號的2階統計特性出發, 采用Jacobi旋轉正交聯合對角化技術, 對空時相關矩陣組進行聯合對角化處理。該方法通過構造合適的聯合對角化結構, 進而對高分辨處理器進行修正, 能夠有效抑制噪聲及干擾的影響, 改善高分辨空間譜估計方法在實際工程應用中的性能。

1 空時相關矩陣聯合對角化結構

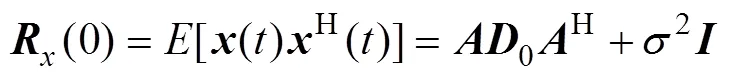
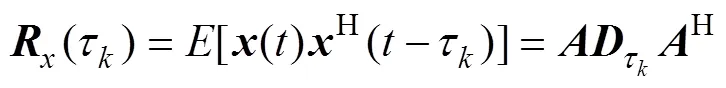
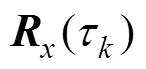
進一步對導向矢量矩陣進行奇異值分解得到

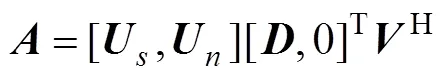
代入式(2)中可得到

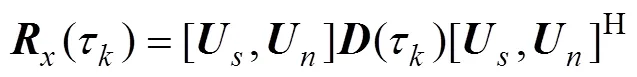
將式(4)的聯合對角化問題簡寫為以下的數學表達式, 從而可以用數學方法解決空間譜估計問題

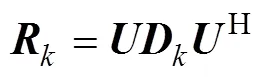
2 基于Jacobi旋轉的空時相關矩陣聯合對角化

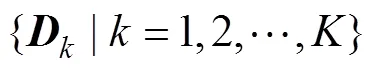
可證明, 聯合對角化問題等價于求解以下的約束最大化問題[17]

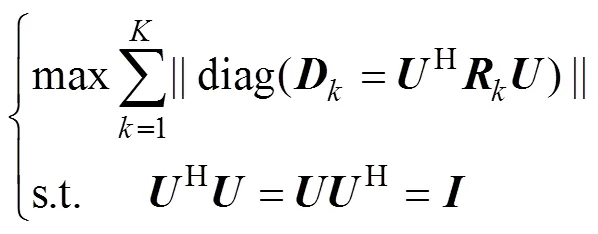
應用基于Jacobi旋轉的正交聯合對角化方法對進行求解, 可將矩陣組的聯合對角化問題轉化為一系列Jacobi旋轉。最終可表示為一系列Jacobi旋轉矩陣乘積的形式。由于聯合對角化矩陣中同時包含了信號子空間和噪聲子空間的全部信息, 因此可以同時利用和進行方位估計。

空時相關矩陣的聯合特征值估計結果為

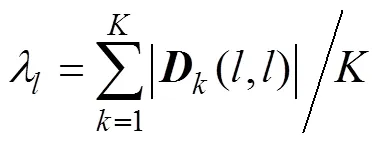
得到修正后的聯合對角化SCB空間譜表示為

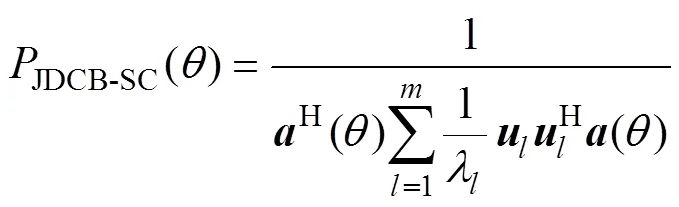
為討論方便, 將基于2階累積量聯合對角化的方位估計方法(joint diagonalization conventional beamforming based on second cumulant, JDCB-SC)。綜上所述, JDCB-SC方位估計方法的信號處理流程見圖1。

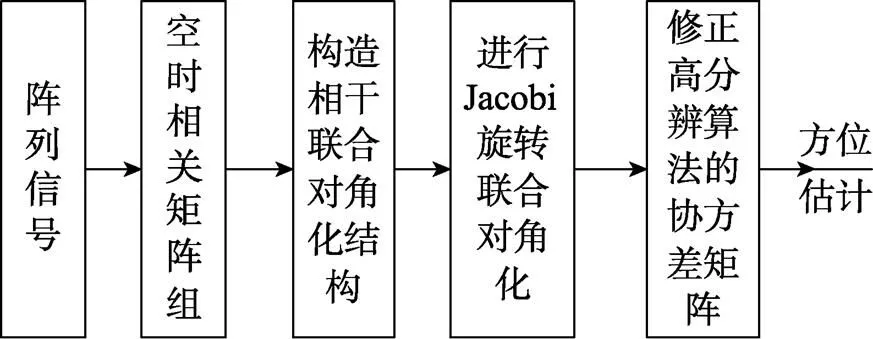
圖1 JDCB-SC算法的信號處理流程圖

3 仿真結果與分析

仿真條件1: 考察對空間方位角靠得很近的雙相干聲源的分辨能力。

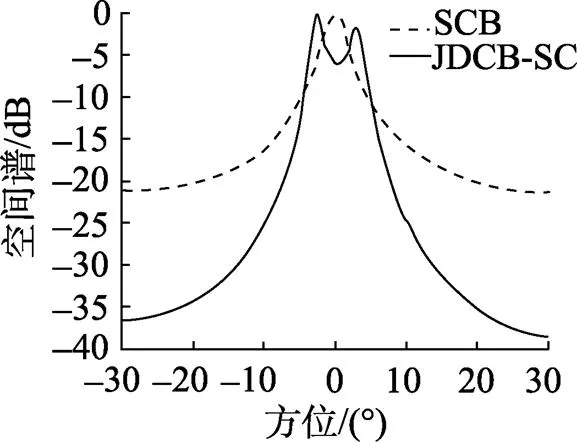
圖2 空間譜估計結果

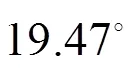
仿真條件2: 不同信噪比條件下的雙相干源方位估計精度。

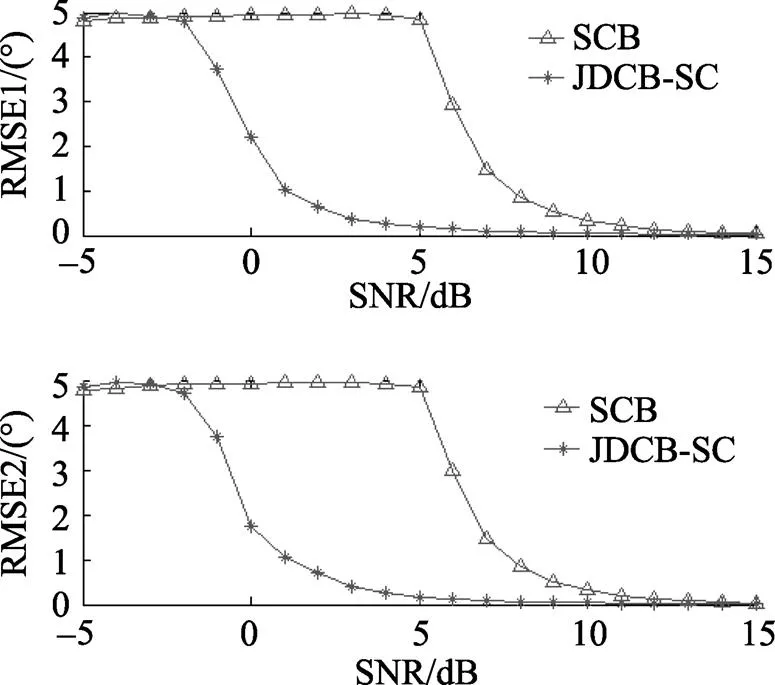
圖3 不同信噪比下的雙相干源方位估計均方根誤差

從圖3可看出, 傳統SCB方法的RMSEs曲線總體上要高于JDCB-SC方法, 特別是在信噪比為-2 ~11 dB這一變化區間。當信噪比小于5 dB時, SCB方法的RMSEs始終較高, 保持5°左右; 而JDCB-SC方法隨著信噪比的減小, RMSEs逐漸增大, 在信噪比約為0 dB時, RMSEs約為2°。當信噪比大于5 dB時, 2種方法的RMSEs都逐漸減小, 而JDCB-SC方法的RMSEs始終較低, 不超過0.2°, 相比之下SCB方法的RMSEs在信噪比約為10 dB時, RMSEs仍保持0.3°。綜上所述, 在相同信噪比條件下, JDCB-SC算法較SCB算法具有較低的方位估計RMSEs, 提高了算法的估計精度。

仿真條件3: 不同快拍數下的雙相干源方位估計精度。

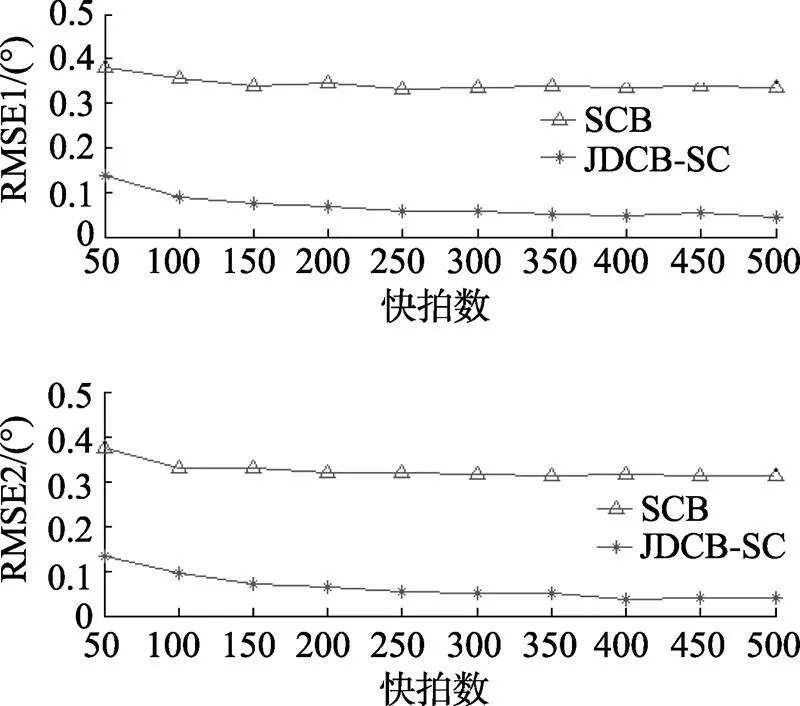
圖4 不同快拍數下的雙相干源方位估計均方根誤差

從圖4中可以看出, 隨著采樣快拍數的增加, SCB和JDCB-SC方法估計目標方位的RMSEs均有所下降, 即在大快拍數條件下, 2種方法的性能均有所改善。在整個快拍數變化的區域中, JDCB-SC方法的RMSEs始終要低于SCB方法的, 兩者相差約為0.25°。綜上所述, 在相同的采樣快拍數條件下, JDCB-SC算法較SCB算法具有較低的方位估計RMSEs, 提高了算法的估計精度。

4 結束語

本文從基陣接收信號的2階統計特性角度出發, 通過Jacobi旋轉正交聯合對角化方法, 構造空時相關矩陣組聯合對角化結構, 重新獲得了聯合特征值并對空間譜進行修正。仿真結果表明, 該方法能夠有效提高常規空間譜估計算法在噪聲、有限采樣效應下的方位估計性能, 具有更高的空間分辨能力及更低的目標方位估計均方根誤差。

[1] 王永良, 陳輝, 彭應寧, 等. 空間譜估計理論與算法[M]. 北京: 清華大學出版社, 2004.

[2] Krim H, Viberg M. Two Decades of Array Signal Processing Research[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.

[3] Capon J. High-resolution Frequency-wave Number Spectrum Analysis[J]. Processing of the IEEE, 1969, 57(8): 1408-1418.

[4] Schmidt R O. Multiple Emitter Location and Signal Parame- ter Estimation[J]. IEEE Transaction, 1986, AP-34(3): 276- 280.

[5] Zoltowski M D. High Resolution Sensor Array Signal Pro- cessing in the Beamspace Domain: Novel Techniques Based on the Poor Resolution of Fourier Beamforming[C]//In Proc. Fourth ASSP Workshop Spectrum Estimation Modeling，1988, 8(1): 350-355.

[6] Xu X L, Buckley K M. Reduced-dirmension Beamspace Broadband Source Localization: Preprocessor Design and Evaluation[J]. In Proc. Fourth ASSP Workshop Spectrum estimation Modeling, 1988, 8(1): 22-27.

[7] Wang H, Kaveh M. Estimation of Angles-of-arrival for Wideband Sources[J]. ICASSP, 1984, 9(1): 279-282.

[8] Hung H, Kaveh M. Focusing Matrices for Coherent Sign- al-subspace Processing[J]. IEEE Transaction on ASSP, 1988, 36(8): 1272-1281.

[9] Gardner W A. Exploitation of Spectral Redundancy on Cycl- ostationary Signals[J]. IEEE Transactions Signal Processing Magazine, 1991, 8(4): 14-37.

[10] Xu G, Kailath T. Direction-of-Arrival Estimation via Explo- itation of Cyclostationarity-A Combination of Temporal and Spatial Processing[J]. IEEE Transactions on SP, 1992, 40(7): 1775-1785.

[11] Leyman A R, Durrani T S. Signal Subspace Processing Using Higher Order Statistics[J]. Electronics Letters, 1994, 30(16): 1282-1284.

[12] Leyman A R, Durrani T S. Signal Subspace Techniques for DOA Estimation Using Higher Order Statistics[J]. ICASSP, 1995, 3(1): 1956-1959.

[13] Belouchrani A, Amin M G, Abed-Meraim K. Direction Finding in Correlated Noise Fields Based on Joint Block Diagonalization of Spatio-Temporal Correlation Matrices[J]. IEEE Signal Processing Letters, 1997, 4(9): 266-269.

[14] 蔣飚, 朱埜, 孫長瑜. 基于空時相關陣聯合對角化的高分辨方位估計. 哈爾濱工程大學學報. 2005, 26(6): 773-776. Jiang Biao, Zhu Ye, Sun Chang-yu. High-resolution Direction Finding Based on Joint Block-diagonalization of Spatio- temporal Correlation Matrice[J]. Journal of Harbin Engin- eering University. 2005, 26(6): 773-776.

[15] 蔣飚. 基于空時相關陣聯合對角化的子空間DOA估計. 聲學與電子工程[J]. 2006, 27(Z): 1-3.

[16] 宋海巖, 樸勝春. 基于高階累積量矩陣組正交聯合對角化的高分辨方位估計方法[J]. 電子與信息學報. 2010, 32(4): 967-972. Song Hai-yan, Piao Sheng-chun. DOA Estimation Method Based on Orthogonal Joint Diagonalization of High-order Cumulant[J]. Journal of Electronics & Information Tech- nology. 2010, 32(4): 967-972.

[17] Cardoso J F, Souloumiac A. Jacobi Angles for Simultaneous Diagonalization[J]. SIAM J Mat Anal, 1996, 17(1): 161-163.

Application of Joint Diagonalization Technology to Spatial Specturm Estimation

ZHAO Long-long1, SONG Hai-yan2

(1.91388thUnit, The people′s Liberation Army of China, Zhanjiang 524022, China；2. College of Electrical and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China )

In practical engineering applications, the performance of conventional spatial spectrum estimation method gets degraded due to the effects of noise, interference and sampling effect, etc. In order to reduce these effects on direction of arrival (DOA) estimation, this paper uses the joint diagonalization to construct the joint diagonalization structure of the spatial-time correlation matrix groups, and obtains a spatial spectrum estimation method based on Jacobi rotation orthogonal joint diagonalization. Thus, corresponding eigenvalues and eigenvectors are utilized to obtain the revised covariance matrix, and the spatial spectrum estimator is revised. Simulation results show that, under different signal to noise ratio(SNR) and snapshots, the proposed method can significantly improve the DOA estimation performance of the conventional spatial spectrum estimation method.

spatial spectrum; joint diagonalization; Jacobi rotation; space-time correlation matrix groups; direction of arrival(DOA) estimation

TJ630.34; TB556

A

1673-1948(2012)05-0344-04

2012-03-13;

2012-04-01.

趙龍龍(1976-), 男, 碩士, 工程師, 研究方向為水聲工程.

(責任編輯: 楊力軍)