輕型反潛魚雷最優(yōu)垂直命中末彈道設計

聶衛(wèi)東, 高智勇, 劉艷波

?

輕型反潛魚雷最優(yōu)垂直命中末彈道設計

聶衛(wèi)東, 高智勇, 劉艷波

(中國船舶重工集團公司第705研究所, 陜西 西安, 710075)

在輕型反潛魚雷最優(yōu)垂直命中彈道設計中, 基于龐特里亞金(Pontryagin)極小值原理解析求解得到的最優(yōu)垂直命中導引律具有理論基礎完備、形式簡潔等優(yōu)點, 但因其推導過程進行了一系列簡化處理, 適用范圍變窄, 且控制系數不易獲得, 事實上難于直接應用。為此, 本文提出了一種實用的魚雷最優(yōu)垂直命中末彈道的設計方法, 即對上述導引律進行面向工程應用的二次優(yōu)化設計, 從而得到滿足不同初始作戰(zhàn)態(tài)勢下的最優(yōu)導引律。通過彈道數字仿真驗證了該方法的可行性和可靠性。分析了末彈道優(yōu)化系統(tǒng)的設計靈敏度, 提出了合理的優(yōu)化設計建議。

輕型反潛魚雷; 垂直命中; 龐特里亞金極小值原理; 末彈道優(yōu)化; 導引律

1 垂直命中含義及指標

隨著現代潛艇防護能力的日益提高, 以有限的魚雷戰(zhàn)斗部裝藥量和傳統(tǒng)的全向爆破方式越來越難以有效地毀傷潛艇。為使魚雷有限裝藥量的戰(zhàn)斗部達到最大的爆破效果, 提出以觸發(fā)定向聚能爆破方式對潛艇實施攻擊, 從而大大提高反潛魚雷的毀傷概率。而要最大限度發(fā)揮定向聚能爆破的效力, 則要求魚雷盡可能垂直命中目標。魚雷垂直命中目標理論上的含義是指, 魚雷命中目標時, 其縱軸線垂直于目標殼體上命中點的切平面, 即魚雷戰(zhàn)斗部定向爆破方向為此平面的法線反方向。在現有技術條件下, 魚雷自導系統(tǒng)一般無法精確測量并給出預計命中點切平面的法線方向, 而能夠較為準確地測量出目標水平面內的航向, 基于此, 工程上“垂直命中”的含義為魚雷命中目標時, 其縱軸線垂直于目標瞬時水平航向。

不同的反潛魚雷有其不同的聚能裝藥形式和爆破控制方式, 因此垂直命中指標也各有不同。本文設計的魚雷最優(yōu)垂直命中末彈道的指標: 將潛艇目標簡化為質點, 雷目質心距離小于某一設定脫靶量時認為魚雷命中目標, 此時魚雷航向與目標航向之間夾角處于所要求的正交范圍內。

2 魚雷垂直命中末彈道起始條件

實現魚雷垂直命中目標的導引彈道稱為垂直命中末彈道, 魚雷垂直命中末彈道的起始點指魚雷穩(wěn)定跟蹤目標, 自導系統(tǒng)探測并確認真實目標, 完成目標尺度識別(目標航向精確探測)后轉入垂直命中導引的瞬間。

2.1 攻擊態(tài)勢

進入垂直命中末彈道時, 考慮魚雷自導系統(tǒng)尺度目標識別距離和最優(yōu)導引最小機動距離限制, 末彈道起始雷目距離設定在一定范圍內。在水平面內, 魚雷可在360°范圍內全向攻擊, 在縱平面內, 魚雷或已處于與目標等深(自導估計)攻擊平面內, 或正處于縱平面導引階段, 縱平面導引通常采用追蹤法。

2.2 導引信息

魚雷進入垂直命中末彈道時, 自導系統(tǒng)能夠提供的目標信息包括[1]: 1) 大地坐標系內目標的運動學信息, 包括目標坐標、目標速度、目標航向等; 2) 雷體坐標系內目標的方位信息, 包括視線角、雷目距離、目標水平和垂直方位角等。

3 魚雷最優(yōu)垂直命中導引律

本文所設計的魚雷垂直命中末彈道方案采用基于龐特里亞金(Pontryagin)極小值原理[2-3]的最優(yōu)導引律, 將魚雷最優(yōu)垂直命中問題視為一類最優(yōu)控制問題, 實現魚雷垂直命中目標的過程就是在雷目相對運動學、動力學和魚雷制導模型基礎上采用最優(yōu)控制理論與方法求解最優(yōu)垂直命中控制律的過程。最優(yōu)導引屬于最優(yōu)化的范疇, 簡言之就是尋求目標泛函的極值問題。

3.1 魚雷動力學狀態(tài)方程

將魚雷導引過程的運動學、動力學、制導及環(huán)境特性等所有方面都包含在最優(yōu)導引律的求解問題中, 會使最優(yōu)導引問題復雜到無法解決。為抓住主要矛盾必須進行簡化, 參考相關文獻的處理方式[4-6], 將魚雷導引過程的狀態(tài)方程簡化為1階滯后環(huán)節(jié)。用x,v,a表示魚雷的位移、速度和加速度, 用x,v,a表示目標的位移、速度和加速度, 用和表示雷目相對位移和相對速度。

作為受控系統(tǒng)的魚雷狀態(tài)方程為

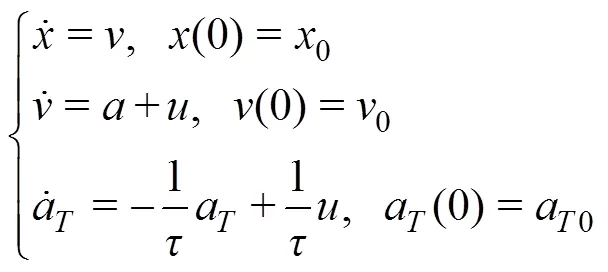
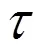
3.2 末彈道最優(yōu)控制律求解

為減小接近目標時魚雷彈道的許用過載, 達到提高垂直命中精度的目的, 垂直命中末彈道采用間接導引法, 首先將魚雷導引到零控曲面[7], 然后由零控曲面到達命中點。其物理含義是, 先將魚雷的航行方向導引到對準預測相遇點, 將全彈道所必需的許用過載集中在此段導引中, 此后只需對魚雷航行進行微調, 即可實現垂直命中。

最優(yōu)垂直命中問題的漢密爾頓函數為[8]

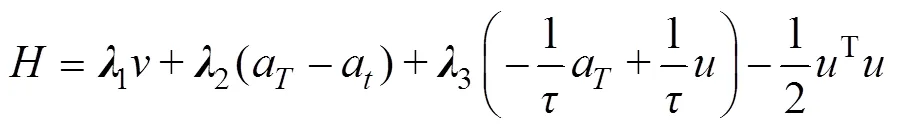
導引終端邊界條件為

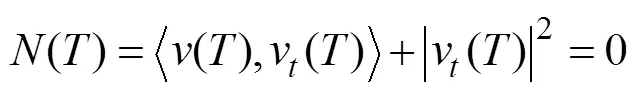
式中:即為零控曲面, 其物理含義是在零控曲面上雷目相對速度矢量和相對位移矢量平行且相反;為比例系數;為導引至零控曲面所用時間。從這種狀態(tài)出發(fā), 即使不加控制(=0)也能達到零脫靶。式(4)表示到達零控曲面時, 魚雷的航向與目標的航向垂直。

略去浩繁的推導過程, 給出水平面最優(yōu)垂直命中導引律為

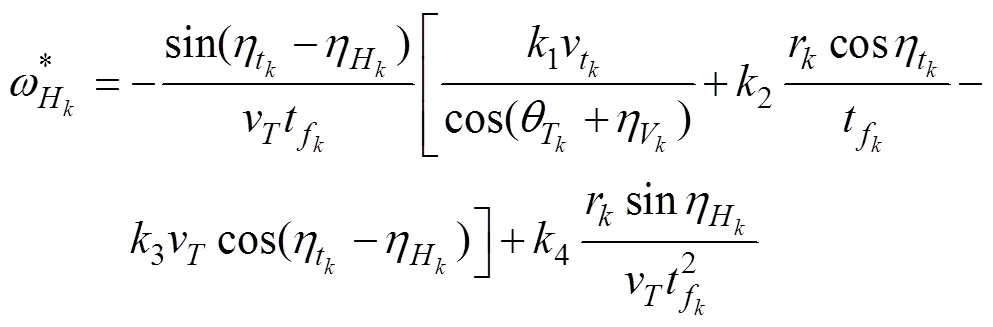
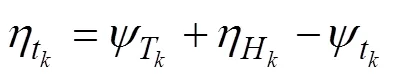
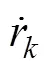
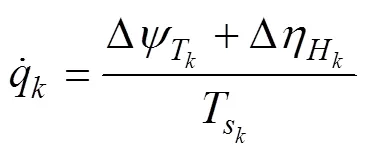
根據古典導引律推導得到垂直面追蹤法導引過程中魚雷的俯仰角速率指令計算式為

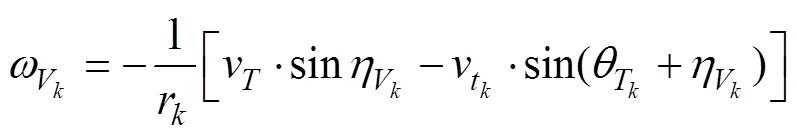
參見魚雷攻擊態(tài)勢圖1, 魚雷末彈道水平面內最優(yōu)垂直命中導引過程為一角速度跟隨控制過程。

4 魚雷最優(yōu)垂直命中導引彈道優(yōu)化設計

雖然基于龐特里亞金極小值原理求解的最優(yōu)垂直命中導引律的理論推導本身就是一個優(yōu)化過程, 但在形成控制律時作了許多簡化, 因而得到的已不是最優(yōu)而是一個次優(yōu)結果, 且不能應用于隨機初始態(tài)勢的情況。因此, 為尋求工程適用的垂直命中導引律, 得到更好的末彈道特性和更高的命中精度, 有必要對上述導引律進行二次優(yōu)化設計, 以滿足工程應用。

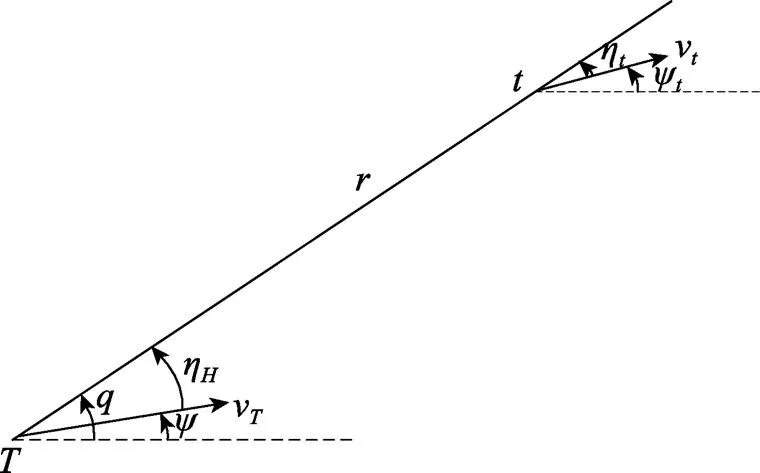
圖1 末彈道雷目水平態(tài)勢圖

4.1 二次優(yōu)化設計問題描述

二次優(yōu)化設計的數學描述如下[9]

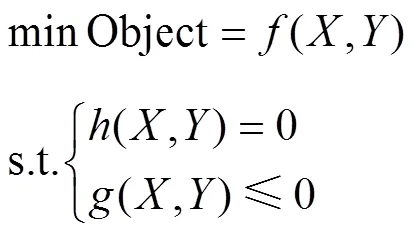
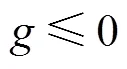
在魚雷最優(yōu)垂直命中彈道優(yōu)化設計中, 優(yōu)化目標為命中角度, 在仿真中為一范圍目標, 即90°±10°指標。優(yōu)化約束為末彈道導引過程中魚雷機動的最大旋回角速度和最大俯仰角速度, 同時優(yōu)化的前提是魚雷命中目標, 因此魚雷最終命中目標也是一項優(yōu)化約束, 在仿真中為一布爾型標志變量。設計變量為式(5)和式(7)中的1,2,3,4和k這5個控制系數, 優(yōu)化設計過程就是尋求最優(yōu)的一組控制系數, 使得式(5)成為適合特定態(tài)勢下的最優(yōu)垂直命中導引律; 當關注子系統(tǒng)時, 也可將子系統(tǒng)的性能參數指定為設計變量, 如魚雷自導系統(tǒng)設計參數或性能參數, 前者考察子系統(tǒng)設計特性, 后者為總體對于子系統(tǒng)的性能要求。

狀態(tài)變量包括魚雷及目標的運動學參數、相對運動學參數(如雷目距離、相對速度等)、導引時間和航程等。系統(tǒng)參數為描述工程系統(tǒng)特征的一組固定參數(或滿足一定分布律的隨機參數), 在設計過程中一般不能為設計者所控制, 如不再更改的系統(tǒng)設計參數和環(huán)境參數等。

4.2 魚雷垂直命中導引彈道優(yōu)化設計數學模型

基于前述, 輕型魚雷機動性能優(yōu)良, 可認為雷體能夠實時響應角速度跟隨控制指令, 并且雷體橫滾能夠得到有效控制, 因此優(yōu)化模型建立在最優(yōu)垂直命中導引彈道階段魚目相對運動學分析基礎之上, 而忽略魚雷和目標的水動力學操控特性, 這有利于將研究關注點集中于不同操控性能魚雷垂直命中彈道優(yōu)化設計的共性問題。

1) 魚雷最優(yōu)垂直命中導引彈道數學模型

魚雷運動學模型用一組代數方程描述如下。

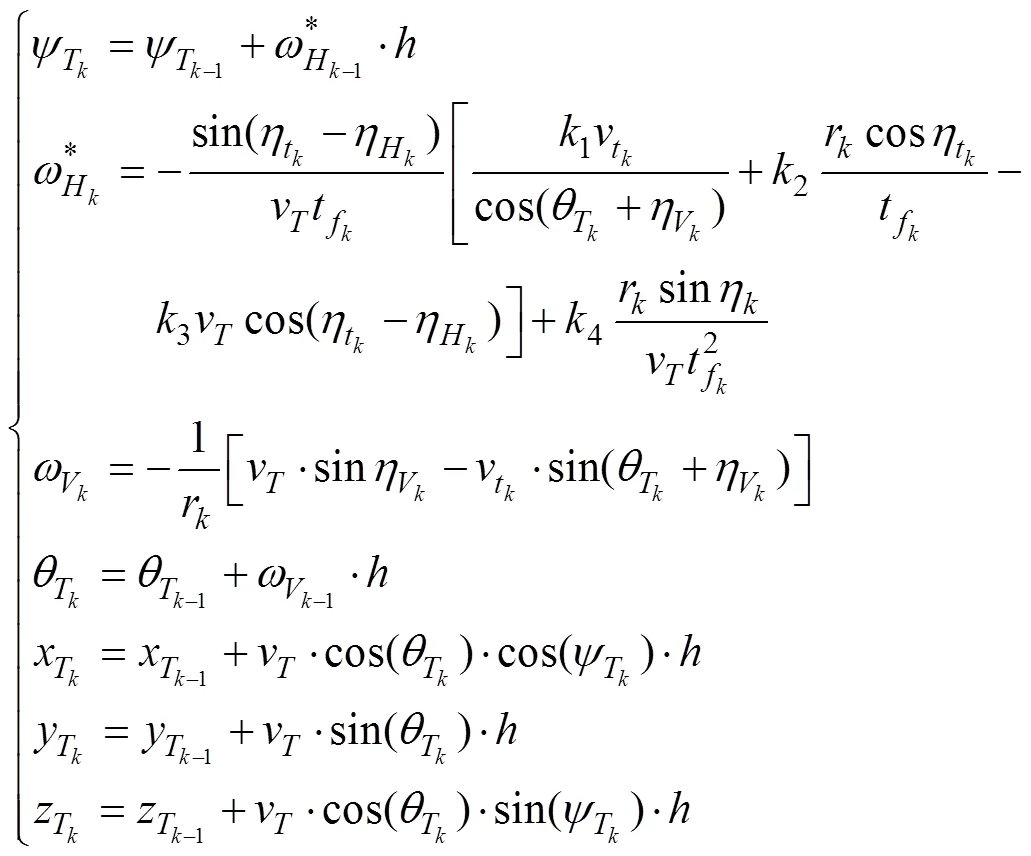
2) 目標運動學數學模型

與魚雷運動學仿真模型類似建立目標的運動學模型如下。

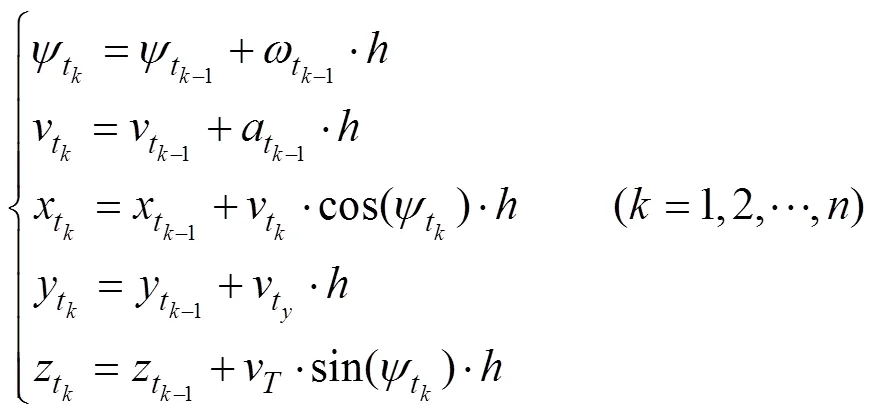
綜上所述, 模型計算受2個時間周期約束,其中魚雷和目標當前運動學參數隨仿真步長推進變化, 而由魚雷自導系統(tǒng)提供的目標運動學參數及其他探測參數隨自導聲周期的推進變化。

4.3 魚雷最優(yōu)垂直命中導引彈道優(yōu)化設計流程

采用MATLAB/SIMULINK建立雷目相對運動學仿真模型, 將仿真模型通過輸入/輸出參數映射與優(yōu)化工具Optimus V9進行連接, 建立優(yōu)化模型。

單一特定作戰(zhàn)態(tài)勢的垂直命中導引彈道優(yōu)化設計沒有實際應用價值, 僅可用于系統(tǒng)性能分析, 因為實際作戰(zhàn)情況千變萬化, 不存在普遍適用的最優(yōu)垂直命中導引彈道方案, 而目前雷上計算機性能還不能滿足在線優(yōu)化計算的實時性要求, 不可能針對每一種作戰(zhàn)態(tài)勢規(guī)劃一種彈道。為使彈道優(yōu)化設計能夠達到實用程度, 必須設計在一定的初始態(tài)勢范圍內適用的最優(yōu)或次優(yōu)垂直命中導引彈道方案, 給出不同初始態(tài)勢范圍內的設計變量, 形成一張魚雷垂直命中彈道射擊參數表, 覆蓋所有可能的初始態(tài)勢。將此表預存于雷上計算機內, 在作戰(zhàn)時便可依據不同的垂直命中彈道初始態(tài)勢選擇彈道方案, 實現垂直命中目標的作戰(zhàn)需求。

為實現任意作戰(zhàn)態(tài)勢下的優(yōu)化設計目標, 需要對基于龐特里亞金極小值原理解析求解得到的最優(yōu)垂直命中導引律進行二次優(yōu)化, 即當系統(tǒng)的狀態(tài)變量和(或)系統(tǒng)參數在接近于工程實際情況的隨機誤差范圍內波動時, 尋求滿足設計要求和設計約束的優(yōu)化結果。二次優(yōu)化計算得到的設計變量除了能夠使優(yōu)化目標達到最優(yōu)外, 還需使其滿足一定的可靠性要求, 比如一定初始態(tài)勢范圍內要求魚雷垂直命中目標的可靠度大于99%, 即要求出現命中角度超出垂直命中指標范圍的可能性小于1%, 在優(yōu)化計算中則表示狀態(tài)變量和(或)系統(tǒng)參數在一定的范圍內按照已知的分布律隨機波動時可容忍的優(yōu)化失效率小于1%。

針對隨機初始作戰(zhàn)態(tài)勢進行最優(yōu)垂直命中彈道的二次優(yōu)化設計流程如圖2所示。

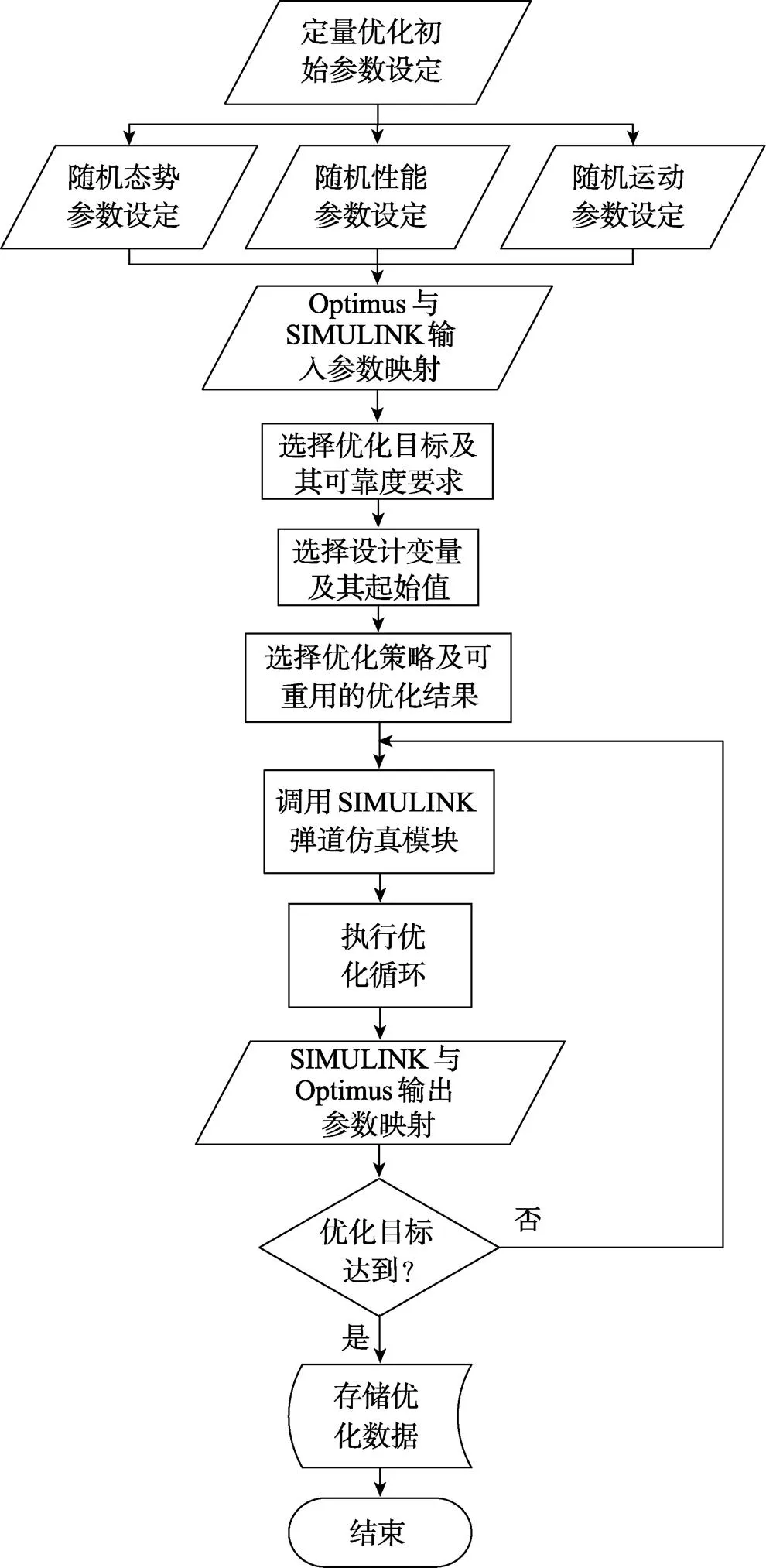
圖2 魚雷垂直命中末彈道二次優(yōu)化設計流程

4.4 魚雷最優(yōu)垂直命中導引彈道優(yōu)化計算

假定目標勻速直航, 在魚雷垂直命中導引開始后不進行機動, 或已完成機動而沿逃逸航向航行, 各輸入參數未加入系統(tǒng)及隨機誤差。初始雷目相對位置分為追擊和迎擊2種態(tài)勢, 如圖3所示。

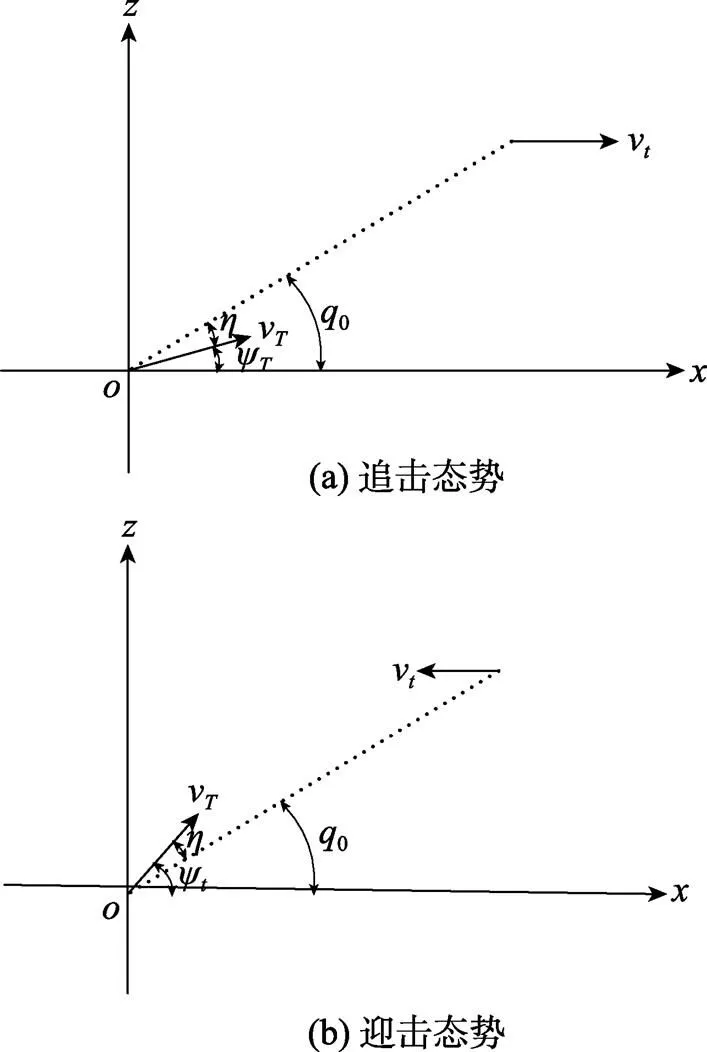
圖3 初始雷目相對位置

作為一個實例, 下面給出一個特定的優(yōu)化計算來進行分析。最優(yōu)垂直命中導引過程是一個角速度跟隨控制過程, 第1象限的魚雷水平導引彈道與第2, 3, 4象限的彈道類似, 不同之處僅僅在于角速度指令的符號, 因此以下僅討論第1象限的情形。

優(yōu)化計算初始設定、優(yōu)化目標及其可靠度、設計變量及設計約束等見表1和表2。

a) 初始設定

雷目初始視線角由目標相對于魚雷的初始方位決定, 由表可見, 追擊態(tài)勢下第1象限內雷目初始視線角共分為3個區(qū)間進行優(yōu)化計算, 分別是: 15°~30°、30°~60°和60°~90°, 迎擊態(tài)勢下第1象限內雷目初始視線角與追擊態(tài)勢一樣分為3個區(qū)間進行優(yōu)化計算。事實上, 初始雷目距離和目標初始航速也需劃分態(tài)勢區(qū)間, 以得到更為廣泛適用的最優(yōu)控制律, 這里為簡化尋優(yōu)計算而僅對目標初始方位進行了態(tài)勢劃分。需要指出的是, 小視線角初始態(tài)勢下(尤其是目標大航速時)很難得到垂直命中彈道的優(yōu)化設計點, 必須采用其他方法實現垂直命中, 這個問題將在另文中加以討論。

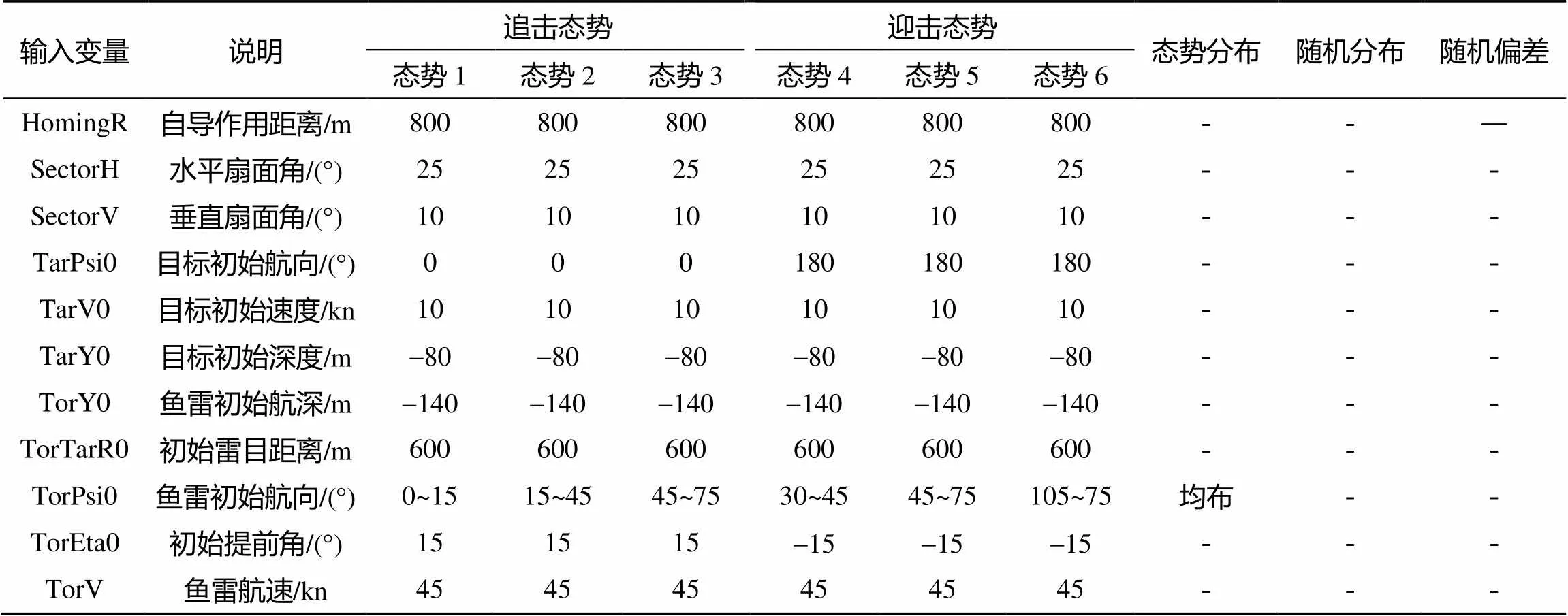
表1 優(yōu)化計算初始設定

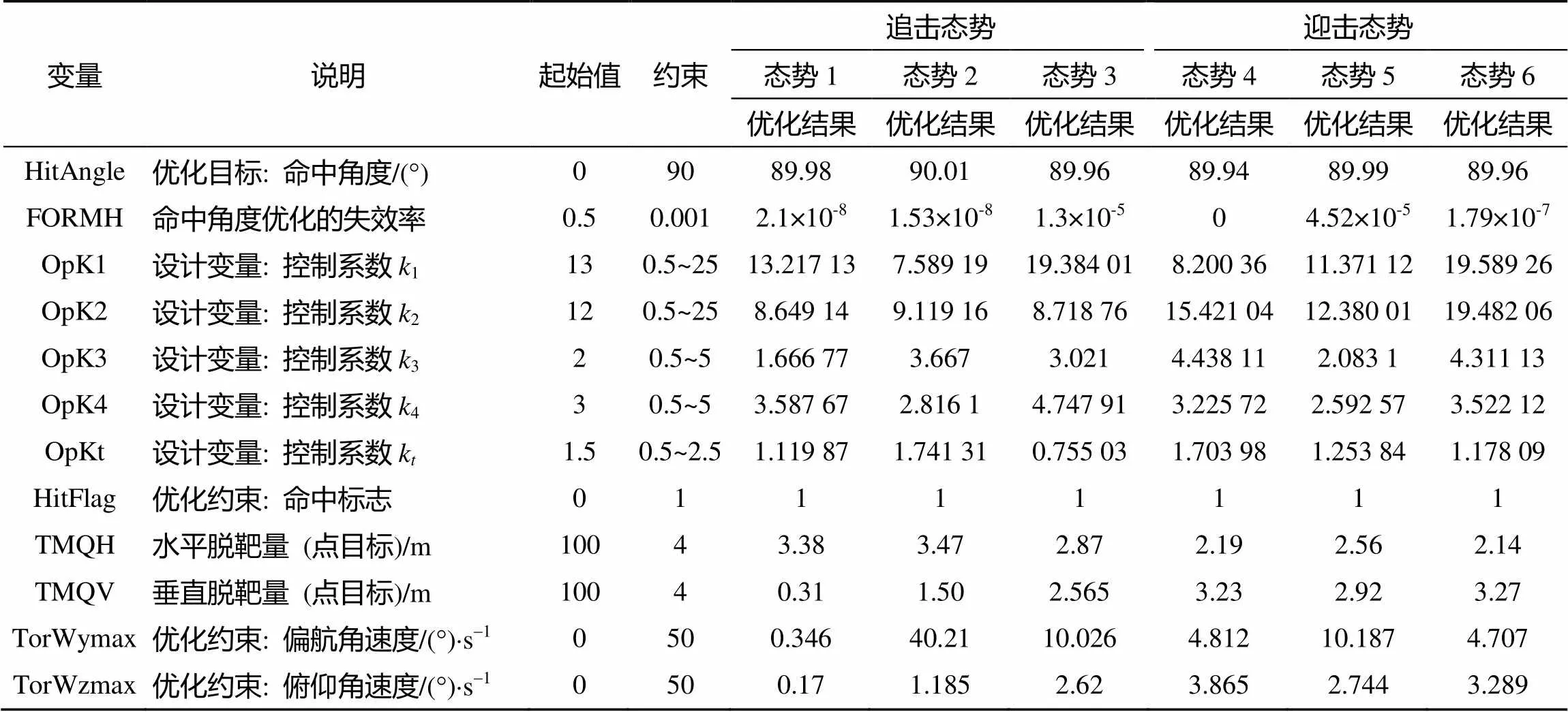
表2 6種初始態(tài)勢下的優(yōu)化結果

b) 優(yōu)化計算及結果輸出

優(yōu)化計算方法選用遺傳算法, 兼顧效率與精度。優(yōu)化計算會得到多組滿足要求的結果, 表2僅列出相對最優(yōu)的一組。

將上述輸入參數及優(yōu)化結果代入末彈道數字仿真程序, 在6種初始態(tài)勢范圍內任意給定一固定態(tài)勢, 運行仿真得到6種態(tài)勢的導引彈道曲線, 圖4僅示出水平面導引彈道。

4.5 系統(tǒng)近似與系統(tǒng)靈敏度分析

在優(yōu)化設計中, 靈敏度分析是指對系統(tǒng)性能因設計變量或系統(tǒng)參數的變化顯示出來的敏感程度的分析[9]。分析系統(tǒng)靈敏度有助于設計者關注影響優(yōu)化設計的主要因素, 從而有針對性地改進設計。通常靈敏度分析不像數學中求函數的偏導數那么簡單, 原因是系統(tǒng)優(yōu)化模型往往不會有顯式形式, 因此通常要對系統(tǒng)進行近似處理以利于分析靈敏度。Optimus中采用基于試驗設計理論(design of experiment theory, DOE)的方法構建系統(tǒng)的多項式擬合近似模型, 在此模型基礎上進行系統(tǒng)靈敏度分析。

對系統(tǒng)進行全參數靈敏度分析結果如表3(附表)所示。表3中橫坐標為待分析參數, 縱坐標為影響參數, 影響度用無因次數表示, 數字越大, 表明影響度越大, 負號表示影響是逆向的。感興趣的是影響優(yōu)化目標命中角度(HitAngleOut)的各參數, 可以看到, 目標速度(TarV0)對優(yōu)化目標產生的逆向影響最大, 目標航速越大, 實現垂直命中的幾率越小, 因此魚雷對抗高速目標時要采取補償措施, 以抵消目標高速的不利影響; 其次是魚雷自導水平扇面角(SectorH), SectorH越大, 魚雷在進行末彈道機動時丟失目標的幾率就越小, 實現垂直命中的幾率就越大; 魚雷機動角速度上限(TorWymax)是在SIMULINK仿真程序中設定的約束條件, 不參與尋優(yōu)過程, 因此其影響也不被衡量; 初始雷目距離(TorTarR0)、魚雷初始航向(TorPsi0)、魚雷初始提前角(TorEta0)決定著初始雷目態(tài)勢, 它們對優(yōu)化目標的影響隨不同態(tài)勢設定而不同, 有時是正向影響, 有時是逆向影響, 需要對每一態(tài)勢劃分區(qū)間進行具體分析; 優(yōu)化目標相對于其他參數的靈敏度較小, 不必特別關注。

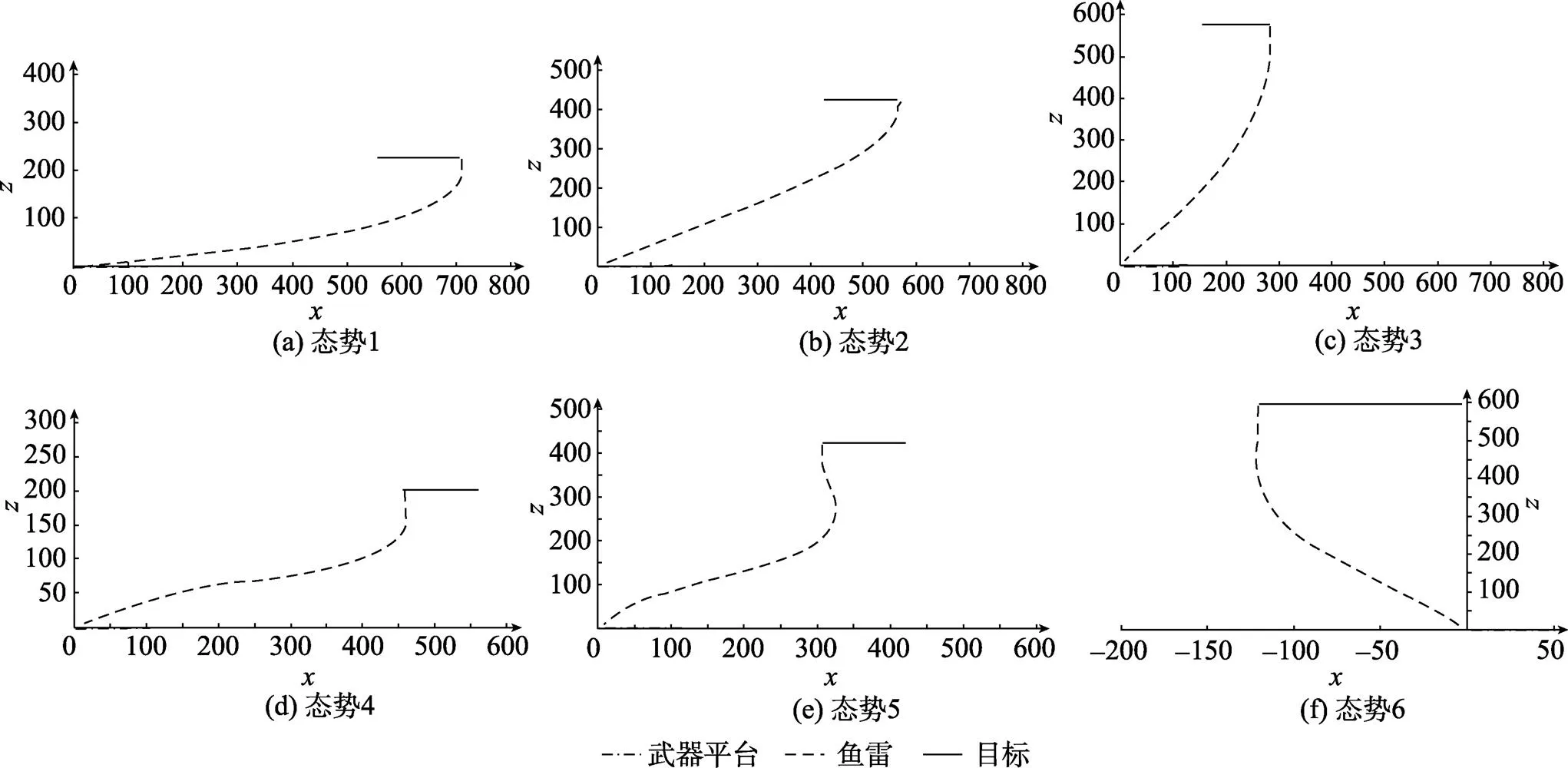
圖4 最優(yōu)垂直命中末彈道仿真曲線

5 結束語

本文提出了一種魚雷最優(yōu)垂直命中末彈道的設計方法, 其基本思想是在末彈道導引過程中保持魚雷與目標的聲學接觸, 對基于龐特里亞金最小值原理解析求得的最優(yōu)垂直命中導引律進行面向工程應用的二次優(yōu)化設計。這樣可以得到適用于不同初始作戰(zhàn)態(tài)勢的一組最優(yōu)導引律, 仿真表明這一方法是可行的, 并獲得了一致性良好的優(yōu)化結果。文中還進行了末彈道優(yōu)化系統(tǒng)的靈敏度分析, 指出了影響最優(yōu)垂直命中末彈道設計的主要因素, 為重復優(yōu)化或改進優(yōu)化提出了建議。

[1] 李志舜. 魚雷自導信號與信息處理[M]. 西安: 西北工業(yè)大學出版社, 2003.

[2] L.D.伯科維茨. 最優(yōu)控制理論[M]. 上海: 上海科學技術出版社, 1985.

[3]劉豹, 唐萬生. 現代控制理論[M]. 三版. 北京: 機械工業(yè)出版社, 2006.

[4] 韓京清. 最優(yōu)導引律[J]. 航空學報, 1979, 14(1): 83-90.

[5] 王朝珠. 帶有不確定因素的最優(yōu)攔截制導律[J]. 航空學報, 1983, 4(4): 70-77. Wang Chao-zhu. An Optimum Intercept Guidance Law with Uncertain Factors[J]. Acta Aeronautica Et Astronautica Sinica, 1983, 4(4): 70-77.

[6] 詹致祥. 考慮一階環(huán)節(jié)和法向約束的最優(yōu)導引律[J]. 航空學報, 1986, 7(3): 291-297. Zhan Zhi-xiang. Optimal Guidance Law wih First Order Lag Loop and Normal Constraint[J]. Acta Aeronautica Et Astro- nautica Sinica, 1986, 7(3): 291-297.

[7] C.J.貝茨. 攻擊機動目標的最優(yōu)制導規(guī)律[M]. 北京: 宇航出版社, 1989.

[8] 詹致祥. 魚雷制導規(guī)律及命中精度[M]. 西安: 西北工業(yè)大學出版社, 1995.

[9] 王振國. 飛行器多學科設計優(yōu)化理論與應用研究[M]. 北京: 國防工業(yè)出版社, 2006.

附表 表3 全參數靈敏度分析

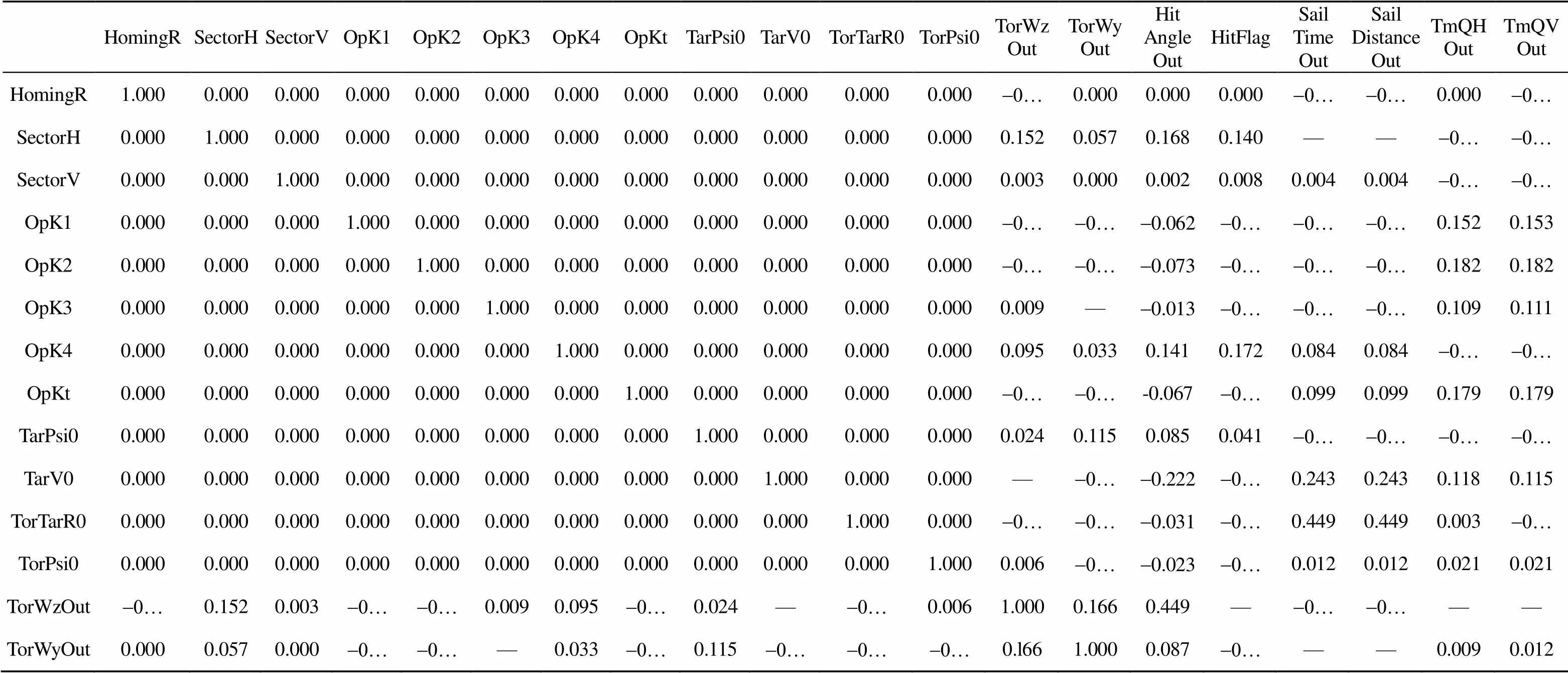
Table 3 System sensitivity analysis with full parameters

Optimization Design of Perpendicular Hit Terminal Trajectory for Lightweight Antisubmarine Torpedo

NIE Wei-dong, GAO Zhi-yong, LIU Yan-bo

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

Although it is more theoretically perfect and compendious than other guidance laws, the optimal perpendicular hit terminal guidance law based on Pontryagin′s minimal principle is more difficult to be applied directly to lightweight antisubmarine torpedo trajectory design for its idealization and indeterminate control coefficients. Accordingly, a practical optimization method is introduced into perpendicular hit terminal trajectory design for a lightweight antisubmarine torpedo in this paper. In this method, engineering-oriented secondary optimization is performed on the guidance law mentioned above to gain optimal guidance laws for different initial operation postures. Digital simulations demonstrate the feasibility and reliability of the proposed method. In addition, the design sensitivity of the terminal trajectory optimization system is analyzed, and suggestions about the optimization design are offered.

lightweight antisubmarine torpedo; perpendicular hit; Pontryagin's minimal principle; terminal trajectory optimization; guidance law

TJ630.2

A

1673-1948(2012)01-0001-08

2011-05-23;

2011-09-02.

聶衛(wèi)東(1972- ), 男, 博士, 研究方向為系統(tǒng)建模與仿真.

(責任編輯: 陳 曦)