格蘊涵代數中的零化子

趙建彬, 朱 華, 陳樹偉

(1.鄭州大學 數學系 河南 鄭州 450001; 2.鄭州大學 電氣工程學院 河南 鄭州 450001)

0 引言

為了建立一個可以進行知識表達和推理的邏輯系統，1993年,徐揚[1]將格與蘊涵代數相結合,提出了格蘊涵代數的概念，并討論了其性質.此后，許多學者對格蘊涵代數進行了大量的研究工作[2-12].例如，Jun等[13]提出了格蘊涵代數中的LI-理想的概念，并研究了其性質.Liu等[4]提出了格蘊涵代數中的ILI-理想與最大LI-理想的概念，研究了它們的性質，并得到了ILI-理想的擴張原理.2006年，朱華等[9]提出了格蘊涵代數中的素理想與準素理想的概念，并研究了它們的性質及它們之間的關系．2008年，Pan等[14]討論了格蘊涵N-序半群與格蘊涵P-序半群中sl理想的性質．作者基于以上工作，在格蘊涵代數中提出了零化子的概念，證明了零化子是理想和sl理想,并討論了零化子的特殊性質及零化子與理想、sl理想和零化子的格蘊涵同態像之間的關系.

1 預備知識

定義1[1]設(L,∧,∨,′)是一個有泛界O，I的有余格,≤是L上的偏序關系,若映射→:L×L→L滿足: 對任意x,y,z∈L,

(I1)x→(y→z)=y→(x→z)；

(I2)x→x=I；

(I3)x→y=y′→x′；

(I4)若x→y=y→x=I，則x=y；

(I5)(x→y)→y=(y→x)→x；

(l1)(x∨y)→z=(x→z)∧(y→z)；

(l2)(x∧y)→z=(x→z)∨(y→z)；

則稱(L,∧,∨,′,→,O,I)是一個格蘊涵代數(簡記為L).若它還滿足：x∨y∨((x∧y)→z)=I,則稱(L,∧,∨,′,→)是一個格H蘊涵代數.

定義2[15]設L是格蘊涵代數，A是L的非空子集，若A滿足：①O∈A；②若(x→y)′∈A,y∈A，則x∈A，稱A為L的理想.

引理1[15]設A為L的理想，如果?x,y∈L,x≤y,y∈A，則x∈A．

定理1[15]設Αi是L的一組理想(i=1,…,n)，則∩Ai也是L的理想.

設A?L，則包含A的最小理想稱為由A生成的理想,記作A?.特別地,若A={a},記A?=a?.

定理2[15]設L1和L2是格蘊涵代數,f:L1→L2是L1到L2的映射,若?x,y∈L1,f(x→y)=f(x)→f(y),則稱f為從L1到L2的蘊涵同態.若蘊涵同態f還滿足：f(x∨y)=f(x)∨f(y),f(x∧y)=f(x)∧f(y),f(x′)=(f(x))′,則稱f為從L1到L2的格蘊涵同態.

若格蘊涵同態映射f是一一映射，則稱f為格蘊涵同構映射.

定義3[14]設A是L的非空子集,如果①AL,LA?A; ②?a∈A,b∈L,如果b≤a，則b∈A; ③?a,b∈A,a∨b∈A,則稱A是L的sl理想.

格蘊涵代數L中，?x,y,z∈L,有以下結論[15]：①x→y≤(y→z)→(x→z),x→y≤(z→x)→(z→y);②若x≤y，則y→z≤x→z,z→x≤z→y;③x∨y=(x→y)→y.

2 格蘊涵代數中的零化子

定義4設L是格蘊涵代數,B是L的非空子集,如果B*={x∈L|?b∈B,x∧b=O},則稱B*為B的零化子.

例1[15]設L={0,a,b,c,d,1}是圖1所示的偏序集.定義L上的余運算為:0′=1,a′=c,b′=d,c′=a,d′=b,1′=0.L的蘊涵運算“→”的定義見表1,則(L,∧,∨,′,→)構成一個格蘊涵代數.

令B={0,c},則B*={0,a,d}.

例1說明格蘊涵代數中的零化子的確存在.

注顯然{O}的零化子是L.

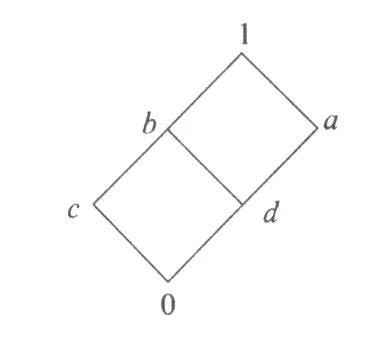
圖1 L的偏序集Fig.1 Hasse diagram of L

→0abcd10111111ac1bcb1bda1ba1caa11a1db11b1110abcd1

下面給出零化子的重要性質.

定理3設L是格蘊涵代數,B為L的非空子集,若B*為B的零化子,則?x∈L,b∈B,x→b=x′?x∈B*.

證明“?” 因為?x∈L,b∈B,x→b=x′,則(x→b)→x′=I,所以(b′→x′)→x′=b′∨x′=I.則x∧b=O,故x∈B*.

“?” ?x∈B*,b∈B,則x∧b=O，所以(b∧x)′=b′∨x′=(b′→x′)→x′=I，故b′→x′≤x′，b′→x′≥x′顯然成立.所以b′→x′=x′,即x→b=x′.

定理4設L是格蘊涵代數,a∈L,則?x∈(a)*,a≤x′.

證明因為x∈(a)*,由定理3知,x→a=x′.又因為x′∨a→(x→a)=(x′→(x→a))∧(a→(x→a))=(a′→(x′→x′))∧(x→(a→a))=I,所以x′∨a≤x→a,則x′≤x′∨a≤x→a=x′,故x′∨a=x′，則a≤x′成立.

下面證明零化子是理想和sl理想.

定理5設L是格蘊涵代數,B為L的非空子集,若B*為B的零化子,則B*為L的理想.

證明顯然O∈B*.?x,y∈L,若(x→y)′∈B*,y∈B*,由定理3知，?b∈B,y→b=y′,(x→y)′→b=x→y.則x′=I→x′=((y→b)→y′)→x′=((b′→y′)→y′)→x′=(b′∨y′)→x′=(b′→x′)∧(y′→x′)=(b′→x′)∧(x→y) =(b′→x′)∧((x→y)′→b)=(b′→x′)∧(b′→(x→y))=(b′→x′)∧(b′→(y′→x′))=b′→x′=x→b.

由定理3知,x∈B*,所以B*為L的理想.

定理6設L是格蘊涵代數,B為L的非空子集,若B*為B的零化子,則B*為L的sl理想.

證明由定理5與文獻[14]中的定理4.2,顯然可得.

接下來給出零化子的特殊性質.

定理7設L是格蘊涵代數,B,C是L的非空子集,則下列性質成立:①若B?C,則C*?B*;②B?B**;③B*=B***;④(B∪C)*=B*∩C*.

其中,B*是B的零化子，B**表示B*的零化子.

證明①?x∈C*,則?c∈C,x∧c=O.因為B?C,所以?b∈B,x∧b=O，則x∈B*，故C*?B*成立.

②?b∈B,x∈B*,x∧b=O,則b∈B**,故B?B**.

③由②知,B*?B***,B?B**.由①知,B***?B*，所以B*=B***.

④因為B?B∪C,C?B∪C,由①知,(B∪C)*?B*,(B∪C)*?C*，則(B∪C)*?B*∩C*.另一方面,又因為?x∈B*∩C*,所以x∈B*且x∈C*，則?b∈B∪C，b∈B或b∈C,都有x∧b=O,因此x∈(B∪C)*.即B*∩C*?(B∪C)*，故(B∪C)*=B*∩C*.

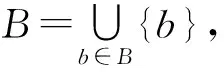
推論2設L是格蘊涵代數,A,B是L的非空子集,則A*∩B*?(A∩B)*.

證明由定理7中④知,A*∩B*=(A∪B)*.因為A∩B?A∪B,則由定理7中①知,(A∪B)*?(A∩B)*，故A*∩B*?(A∩B)*.

定理8設L是格蘊涵代數,B是L的非空子集，B?是B的生成理想，若B?=B?**,則B?=B**.

證明因為B?B?,由定理7中①知，B?*?B*,B**?B?**,又因為B?=B?**,所以B**?B?.

另一方面,由定理7中②知，B?B**,由定理5知,B**是L的理想,所以B??B**.綜上,B?=B**.

定理9設A,B是L的非空子集,則A*∪B*??(A∩B)*.

證明因為A∩B?A,A∩B?B,由定理7中①知，A*?(A∩B)*,B*?(A∩B)*,故A*∪B*?(A∩B)*.由定理5知，(A∩B)*是L的理想,故A*∪B*??(A∩B)*.

定理10設L是格蘊涵代數,若B為L的理想,則B∩B*={O}.

證明顯然O∈B∩B*.?x∈B∩B*,則x∈B且x∈B*.所以x=x∧x=O.

下面給出零化子與理想之間的關系.

定理11設B是L的非空子集，C為L的理想,則B∩C={O}?B?C*.

證明“?” 若B∩C={O},則?x∈B，c∈C,x∧c=O.否則x∧c≠O∈B∩C與前提矛盾.所以x∈C*，即B?C*.

“?” 因為B?C*,則B∩C?C*∩C,由定理10知,C*∩C={O}.故B∩C={O}.

定理12設B,C是L的非空子集,若C=C**,則B?C?B∩C*={O}.

證明“?” 由定理7知,C*是L的理想.又因為B?C,再由定理11知,B∩C*={O}.

“?” 因為B∩C*={O},由定理11知,B?C**=C.

最后給出了零化子與其格蘊涵同態像之間的關系.

定理13設(L,∧,∨,→,′,O,I),(L1,∧1,∨1,→1,1,O1,I1)是格蘊涵代數,B為L的非空子集,f:L→L1是格蘊涵同態,若B*是B的零化子,則f(B*)?f(B)*.

證明?y∈f(B*),則?x∈B*?L,使f(x)=y.又因為B*是B的零化子,所以?b∈B,x∧b=O，則f(x∧b)=f(x)∧1f(b)=O1，即?z∈f(B),?t∈B,使得f(t)=z.由y∧1z=f(x)∧1f(t)=f(x∧t)=O1知，y∈f(B)*.故結論成立.

定理14設L,L1是格蘊涵代數,B為L的非空子集,f:L→L1是格蘊涵同構,若B*為B的零化子,則f(B*)=f(B)*.

證明由定理13知，f(B*)?f(B)*.下面只需證明f(B)*?f(B*).

?y∈f(B)*，?y1∈f(B),使y∧1y1=O1，并且?x∈L,x1∈B，使y=f(x),y1=f(x1)，因此y∧1y1=f(x)∧1f(x1)=f(x∧x1)=O1.

因為f:L→L1是格蘊涵同構，故x∧x1=O，所以x∈B*，因此y=f(x)∈f(B*)，即f(B)*?f(B*).

參考文獻：

[1] 徐揚. 格蘊涵代數[J]. 西南交通大學學報,1993，28 (1): 20-27.

[2] Liu Jun， Xu Yang. Filters and structure of lattice implication algebra[J]. Chinese Science Bulletin, 1997, 42(18): 1517-1520.

[3] Ma Jun, Li Wenjiang, Ruan Da, et al. Filter-based resolution principle for lattice-valued propositional logicLP(X)[J]. Information Sciences, 2007, 177(4): 1046-1062.

[4] Liu Yonglin, Liu Sanyang, Xu Yang, et al.ILI-ideals and primeLI-ideals in lattice implication algebras[J]. Information Sciences, 2003,155(1/2): 157-175.

[5] Jun Y B, Xu Yang, Ma Jun. Redefined fuzzy implicative filters[J]. Information Sciences, 2007, 177(6): 1422-1429.

[6] 王學芳.基于格蘊涵代數的格值邏輯及其模型論的研究[D]. 成都:西南交通大學, 2004.

[7] Xu Yang, Qin Keyun, Liu Jun, et al.L-valued propositional logicLvpl[J]. Information Sciences, 1999, 114(1/2/3/4): 205-235.

[8] Xu Yang, Liu Jun, Song Zhenming, et al. On semantics ofL-valued first-order logicLvfl[J]. International Journal of General Systems, 2000, 29(1): 53-79.

[9] 朱華, 趙建彬, 徐揚. 剩余格蘊涵代數中準素理想的研究[J]. 鄭州大學學報:理學版, 2006, 38(2): 25-28.

[10] 朱華, 趙建彬, 徐揚. 剩余格蘊涵代數中n-重素理想的研究[J]. 鄭州大學學報: 理學版, 2008, 40(1): 19-22.

[11] 朱華, 陳樹偉. 格蘊涵代數中多重模糊正關聯濾子的研究[J]. 鄭州大學學報:理學版,2009, 41(2): 19-23.

[12] Zhu Hua, Du Weifeng, Zhao Jianbin. The annihilator and its structure in lattice implication algebras[C]//Proceedings of the 2nd International Symposium on Networking and Network Security. Jinggangshan, 2010: 206-209.

[13] Jun Y B, Roh E H, Xu Yang.LI-ideals in lattice implication algebras[J].Bull Korean Math Soc, 1998,35 (1):13-23.

[14] Pan Xiaodong, Xu Yang. Lattice implication ordered semigroups[J]. Information Sciences, 2008, 178(2): 403-413.

[15] Xu Yang, Ruan Da, Qin Keyun, et al. Lattice-valued Logic[M]. Berlin: Springer-Verlag, 2003:28-98.