考慮負荷管理的供電公司最優競標策略

謝 俊，杜 鵬，章美丹

（1.南京郵電大學自動化學院，南京 210046；2.浙江大學電氣工程學院，杭州 310027）

近年來，供電公司競價策略的研究是一個研究熱點，該領域已經有大量文獻發表［1～3］，為供電公司參與日前市場競爭提供了有益的參考。但是，這些工作無一例外的把重心放在了競價市場的策略性競標行為上，對供電公司的負荷管理措施與競價市場上策略性競標行為的協調問題考慮欠缺。

供電公司推行負荷管理，鼓勵用戶參與“削峰填谷”，可以讓用戶負荷積極響應于批發市場的購電電價，這會給供電公司帶來巨大的經濟效益，實現供電公司與終端用戶的雙贏局面。這樣，供電公司參與市場競爭不同于發電商：一方面供電公司需要開展購電業務，希望找到優化的購電策略，降低購電費用和風險；另一方面供電公司向用戶開展供電業務，需要合理制定負荷管理措施，鼓勵用戶參與到負荷管理措施中來，優化用電方式，降低供電成本，提高總收益。因此，供電公司競標策略的構造與基于用戶響應的負荷管理措施的制定是一個聯動的過程。

本文以概率性市場出清電價預測的預測結果為基礎，首先研究考慮分時電價聯動機制的供電公司競標策略問題，然后研究考慮可中斷負荷管理的供電公司最優競標策略。算例分析反映了本文給出的供電公司最優競標策略的基本特征。

1 市場環境下供電公司的負荷管理

電力商品具有不同于其他普通商品的特殊性［1］：①電能不能大規模存儲且以光速傳輸，電能的生產和消費必須實時平衡；②電能傳輸受物理規律約束，容易發生輸電阻塞。這些特點使得電力交易中批發市場電價很容易受到影響而產生劇烈波動。根據美國紐約電力市場ISO（independent system operator）的歷史記錄，每小時的電力批發價格非高峰季節一天之中高峰電價和低谷電價之比達到2∶1，而在高峰季節這一比例則達到10∶1，某些尖峰（price spike）時段甚至可能更高。

在加州電力市場危機中，有兩家大型供電公司破產，導致其破產的直接原因有兩個［1］：①批發市場電價異常增高，供電公司為滿足終端用戶負荷需求付出了巨額購電費用；②供電公司沒有調節并利用終端用戶的負荷需求彈性。

負荷管理認為用戶負荷不僅可以調節而且部分負荷具有很大的彈性，電力市場的開展為負荷管理注入了新的生機與活力。

1.1 分時零售電價與批發市場電價聯動

零售電價將用戶與供電公司聯系起來，能夠利用并調節用戶的負荷需求彈性，起到平衡市場供求關系的作用［1］。批發市場（長期合同市場與日前市場）電價則把參與市場競爭的各供電公司與各發電商聯系起來，通過發電競價與購電競價使不同條件下的電力生產成本在需求側得到及時體現。公平、合理的電價能夠提供正確的經濟信號，實現電力資源的優化配置。在完全競爭的市場中，批發市場電價與零售電價均不應受到限制，否則會降低市場配置資源的效率。加州電力市場危機中由于凍結了零售電價，同時要求供電公司從競爭的批發市場中購電，導致兩家較大的供電公司破產。“凍結零售電價”使用戶無法響應于批發市場電價，使電價的杠桿作用受到人為阻礙。然而，由于經濟、政治以及社會影響等原因，供電公司向用戶推行實時電價尚不能普遍為用戶所接受。分時電價TOU（time of use）通過不同時段實行不同電價，鼓勵用戶進行負荷調整以改善負荷曲線，實現“削峰填谷”，最終達到減少運行和投資費用的目的。這樣，供電公司有必要建立批發市場電價與分時電價的聯動機制，通過及時調整分時電價，調動用戶響應于批發市場電價的積極性，引導用戶的電力消費。

近年來，市場環境下的分時電價問題已經成為研究熱點，主要集中在峰谷時段的劃分，分時電價制定和市場機制等方面。文獻［4］分析了傳統分時電價在市場環境下的特點，建立了供電公司向用戶售電的分時零售電價與批發市場購電電價的聯動機制，研究表明分時電價與批發市場電價的聯動有利于電力資源的優化配置。

1.2 可中斷負荷管理

可中斷負荷IL（interruptible load）管理是負荷管理的有效手段之一，已經在實踐中取得了較好的效果。在市場環境下，供電公司可以將可中斷負荷作為調節負荷需求的有效手段，增加負荷彈性，實現削峰填谷，規避批發購電電價增高帶來的高額購電費用，減小運行成本，提高經濟效益。

對可中斷負荷管理的研究，早期的工作主要是從負荷管理、提高經濟效益的角度進行的［2，3］。近年來，人們的研究重點轉移到了市場環境下的可中斷負荷問題，這包括可中斷參與市場競爭的競價機制［6］、可中斷負荷的合同管理及定價［7］、可中斷負荷中的激勵機制［8］等。

2 市場出清電價的概率性預測

常規的MCP預測結果一般都是確定性的，只是給出一個確定的值，其缺點是無法給出未來交易時段MCP可能的波動范圍。實際上，由于預測問題的超前性，實現概率性的MCP預測更符合客觀要求，這可應用于競標策略的風險分析。

本文研究考慮負荷管理的供電公司最優競標策略，基于概率性MCP預測的預測結果［9，10］。

表1給出了美國Ontario電力市場2004年4月4日日前市場第13交易時段的MCP概率性預測結果［9］。其中，“0.95＋”表示該預測值大于期望值的置信度為0.95，“0.95－”表示該預測值小于期望值的置信度為0.95，其余依次類推。

表1 Ontario日前市場某一交易時段MCP的概率性預測Tab.1 Probabilistic MCP forecasting of Ontario day－ahead electricity market

3 供電公司批發市場最優購電量

供電公司從長期合同市場與日前市場兩個交易市場購電，其購電成本C1包括長期合同市場與日前市場兩部分。供電公司僅在長期合同市場中與發電公司簽訂了差價合約，差價合約電量在整個購電量中所占的比例γ以及差價合約的敲定價（strike price）已經由供電公司與發電公司預先簽訂。假設供電公司的總電量需求為WD，在交易時段t內長期合同市場、日前市場電價分別為YL（差價合約敲定價）和YS，供電公司相應的購電量為WL（差價合約購電量）和WS，不計損耗時，WD＝WL＋WS。則供電公司在該時段的購電成本為

即

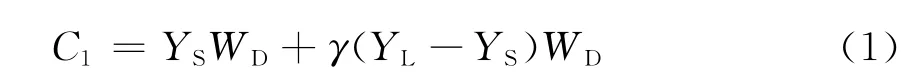
3.1 情形1（考慮分時電價聯動機制）

供電公司的運營業務可以分為兩部分：與配電網相關的業務和與售電相關的業務，前者包括為滿足用戶供電需要進行的配電設施、設備的新建、維護等，后者包括從批發市場購電和向用戶售電。相應的運營成本包括：購電成本、配電容量成本以及配電運行成本等。配電運行成本（包括損耗、人工費用等）可通過會計核算分攤到最終的銷售電價中。

配電容量成本C2根據配電系統容量不足概率LOLP（loss of load probability）計算，表達式為

式中，k為容量成本系數，且有

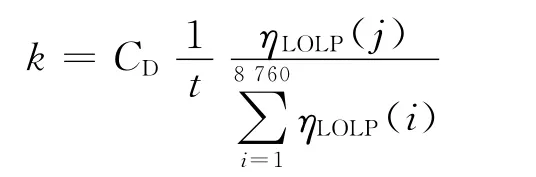
式中：CD為滿足供電專營區配電系統容量增長，平均每年每兆瓦的投資成本；ηLOLP（j）為j時刻配電系統容量不足的概率［2］。

在分時電價的時段劃分上傳統的劃分依據是負荷曲線。市場條件下，供電公司作為自負盈虧的市場經濟主體，考慮到批發市場電價的波動性，購電成本曲線應成為劃分時段的重要依據。本文主要討論考慮分時電價聯動機制的供電公司競標策略問題，并不詳細探討分時電價時段的劃分。

供電公司供電專營區內的終端用戶一般有居民用戶、商業用戶和工業用戶等幾種類型。由于居民用戶和商業用戶用電特性的局限性，部分居民（商業）用戶并不接受每個交易日均變化的分時電價，而只接受按月或按季度為周期變化的分時電價。供電公司在構造次日日前市場競標策略時，對這類終端用戶的零售電價是固定的，本文稱之為第一類分時電價，用YD，f表示，這類用戶的負荷需求稱之為第一類負荷需求，用WD，f表示，該負荷需求可以通過負荷預測得到；其他用戶接受每個交易日均變化的分時電價，本文稱之為第二類分時電價，用YD，v表示，相應的負荷需求稱之為第二類負荷需求，用WD，v表示。

由于負荷需求WD，v與分時電價YD，v相互影響，同時又明顯與溫度、天氣等因素有關，故WD，v可分為兩部分：與價格密切相關的部分Wy和與價格關系不密切、受其他因素影響的部分Wny，滿足關系式WD，v＝Wy＋Wny。其中：Wny可通過負荷預測得到，Wy受價格彈性約束，Wy＝aYD，v＋b，參數a、b為該時段決定分時電價YD，v與負荷Wy關系的常數，通過對歷史數據的分析可以得到。

假設時段t內分時電價YD，v不變。令T＝nt，n＝1，2，…，N，N為日前市場交易時段數。這樣，時段t內供電公司售電業務的總收入為V＝YDf·WD，f＋YD，vWD，v；忽略損耗、人工等費用，該時段內供電公司的收益π′可以表示為

由式（1）～式（3），不計配電損耗和人工費用時，供電公司在時段T內的總收益π為

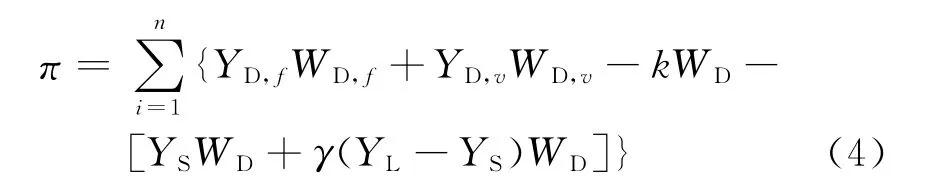
當n＝1時，零售電價與批發市場電價同步聯動，零售電價隨時反映生產成本的變化。當n＞1時，零售電價與批發市場電價不同步聯動，零售電價采用分時電價，不同步變化的零售電價會損失一部分批發市場電價信息。本文取n＝1。

供電公司制定分時電價YD，v的目標，是在滿足一系列約束條件下使時段T內的運營總收益π最大，即

式中，YD，vmax、YD，vmin分別為分時電價YD，v上、下限約束，YD，vmax的是監管部門為防止供電公司通過較高的零售電價牟取暴利而設定的，對監管供電公司的收益水平非常有必要。

當市場出清電價恰為某一置信水平下的預測值時，由該分時電價與購電電價的聯動模型求得供電公司在批發市場的最優購電量為

式中

其中

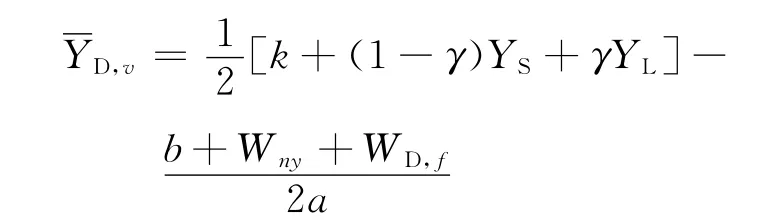
3.2 情形2（考慮可中斷負荷管理）

假設供電公司與N個終端用戶簽定了可中斷負荷合同，中斷電價分別為τ＝（τ1，τ2，…，τn），相應的最大可中斷量分別為當供電公司中斷對終端用戶供電的中斷電量為WⅠ時，為終端用戶i的中斷電量，中斷供電造成供電公司對終端用戶的賠償費用為

供電公司對終端用戶供電的銷售電價為ps，供電量為WD－WⅠ時的售電收入為υ1，則υ1可以描述為

供電公司對終端用戶中斷供電的中斷量為WⅠ時帶來的運行成本的減少為υ2，采用一次函數的形式表示為

式中，K為常數，可以根據供電公司的歷史運營參數，采用統計分析的方法獲得。

針對交易時段t，當長、短期市場電價YL、YS及長期市場購電量在整個購電量中所占的比例γ，供電公司的總電量需求WD，可中斷負荷合同的中斷電價τ和最大可中斷量P已知的情形下，決定每個可中斷負荷的最優中斷電量Pi（即供電公司在批發市場的最優購電量WL＋WS，或可中斷負荷的最優中斷量WⅠ）可以描述為最優化問題，即

式中，λ為售電凈利潤占銷售收入的百分比［2］，0≤λ≤1。

該優化問題的目標函數與約束條件關于決策變量Pi均為線性的，可以采用線性規劃法求解。

4 考慮負荷管理的供電公司競標策略

4.1 基本假設

1）日前市場交易時段數為N（本文取N為24），采用分段競標規則，針對每一交易時段供電公司最多可上報I個競標段（本文取I為9）。

2）日前市場采用統一市場出清電價MCP（market clearing price）結算的定價機制。

3）供電公司處于Price－taker地位，其在日前市場的競標不影響市場出清電價。

4.2 供電公司最優競標策略

供電公司在構造日前市場競標策略時，未來交易時段的市場出清電價是未知的。但是，當市場出清電價恰為某一置信水平下的預測值時，供電公司在批發市場的最優購電量可由上節最優購電量優化模型（5）或模型（10）求得。相應的，供電公司最簡單的競標策略就是向交易中心上報一個競標段，段價就是MCP預測結果的期望值，段容量由上述優化模型求得。但是，這樣的競標策略使得供電公司面臨著巨大的市場運營風險：當實際MCP高于期望值時，供電公司上報的段容量將不能被市場調度，將給供電公司帶來利潤損失；當實際MCP低于期望值時，若該競標段是最后一個被調度的競標段，那么供電公司報一個更低的價格可能獲得更多的利潤。這樣，無論是從規避風險還是從獲得更多利潤的角度出發，供電公司都應該采取一定的策略上報多個競標段。

顯然，供電公司競標越高，其被市場調度的可能性越大；競標越低，其被市場調度的可能性越小。供電公司在構造競標策略時，需要綜合考慮各項成本與回報以及各競標段被市場調度的可能性。基于上述考慮，本文構造供電公司某一交易時段的最優競標策略的基本步驟如下。

步驟1 采用合適的預測工具，預測出該交易時段在9種置信度下的MCP預測值——“0.95＋”、“0.75＋”、“0.50＋”、“0.25＋”、“0”、“0.25－”、“0.50－”、“0.75－”以及“0.95－”。

步驟2 假設MCP為上述置信度下的預測值，應用供電公司在批發市場最優購電量優化模型分別計算每一置信度下的供電公司批發市場最優購電量WL＋WS。

步驟3 以各置信度下的MCP預測值及相應的最優購電量為基礎，生成該交易時段的競標曲線，當出現兩個以上競標段的最優購電量相等時，將這幾個競標段合成為一個競標段，段價為這幾個競標段中最高者，圖1給出了單一交易時段供電公司競標曲線的典型形式。

由此可見，本文構造的供電公司最優競標策略，競標曲線由多個價格－電量對組成，各競標段的段價覆蓋了MCP的典型概率性預測結果，建立了不確定的市場出清電價與確定的競標策略之間溝通的橋梁；同時，決定每個競標段的段容量時考慮了供電公司擁有的可中斷負荷，這使得該競標策略能夠讓供電公司有效規避日前市場的電價波動風險。并且，該方法框架能夠適應于市場要求的任何最多可上報的競標段I，各競標段的段價應該取為哪一置信度下的MCP預測值取決于競標決策時對市場風險的態度。

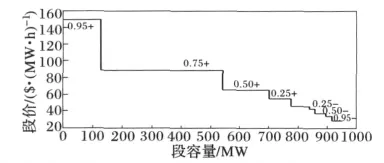
圖1 供電公司競標曲線的典型形式Fig.1 Typical bidding curve of LSE

5 算例分析

5.1 情形1（考慮分時電價聯動機制）

假設所研究的輸配分開電力市場的日交易時段數為24，各交易時段的電價數據見圖2，日前市場各交易時段的概率性MCP預測結果見文獻［9］。供電公司的容量成本系數為12.7＄／（MW·h），第二類分時電價YD，v的電價上限YD，vmax為51.0＄／（MW·h），在各交易時段的負荷彈性參數見表2，整個交易日的負荷預測曲線如圖3所示。

給定差價合約電量在整個購電量中所占的比例γ為0.70，采用本文給出的競標策略進行仿真計算，各交易時段的分時零售電價如圖2所示，各交易時段的利潤如圖4所示，其中實際利潤是基于概率性MCP預測結果取得的，理想利潤是假設準確無誤的預測到市場出清電價時取得的。

圖2 差價合約、日前市場電價和分時零售電價曲線Fig.2 Price curves of contract for difference，day－ahead，and time－of－use

圖3 負荷預測曲線（情形1）Fig.3 Load forecasting curves under（case 1）

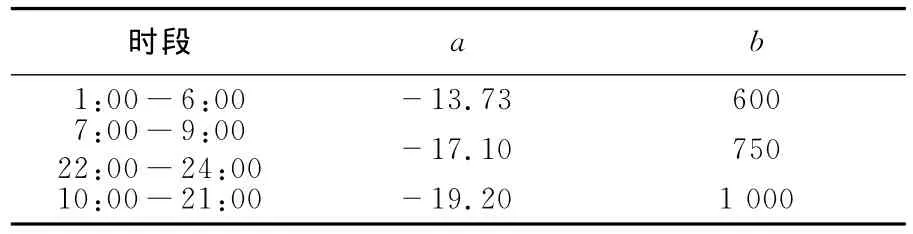
表2 負荷彈性參數Tab.2 負荷彈性參數

由圖2可見，供電公司向用戶售電的第二類分時電價基本上與批發市場購電電價同步變化，表明第二類分時電價能夠引導電力資源在需求側的優化配置。

圖4 供電公司各交易時段的利潤Fig.4 LSE＇s profit under all period of trading

由圖4可見，實際利潤與理想利潤的比值最大值為100.0%，最小值為88.61%，平均值為98.93%，表明了本文給出的競標策略的有效性。

當分時電價YD，v最高限價YD，vmax分別為47、48、49、50、51＄／（MW·h）時，供電公司在整個交易日的利潤如圖4所示。由圖5可見，YD，vmax越低，供電公司的利潤越少，監管部門可以通過分時零售電價的最高限價來防止供電公司通過高零售電價的手段牟取暴利，從而控制供電公司的收益，保護用戶的利益。

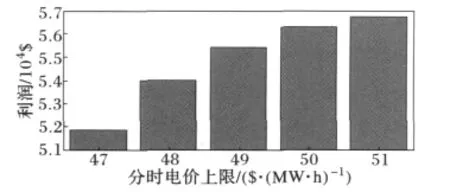
圖5 分時電價上限對供電公司利潤的影響Fig.5 Impact of up－limit of TOU to LSE＇s profit

當差價合約電量在整個購電量中所占的比例分別為0、0.70、0.90時，供電公司在第21交易時段的競標曲線如圖6所示。由圖6可見，差價合約電量在整個購電量中所占的比例越高，供電公司的第一個競標段段容量增加，供電公司在日前市場上的策略性競標行為減少，這是因為差價合約有保證供電公司購電量和規避風險的作用。

圖6 不同差價合約購電量下的供電公司競標曲線Fig.6 LSE＇s bidding curve under different purchasing quantity at contract for difference

5.2 情形2（考慮可中斷負荷管理）

假設所研究的輸配分開電力市場的日交易時段數為24，各交易時段的電價數據見圖7，日前市場各交易時段的概率性MCP預測結果可以在文獻［9］中找到。供電公司對終端用戶供電的銷售電價為0.35＄／（k W·h），υ2的一次項系數K為0.113＄／（k W·h），售電凈利潤占銷售收入的百分比λ為0.89，整個交易日的負荷曲線見圖8。該供電公司與7家終端用戶簽定了可中斷負荷合同，中斷電價向量τ＝（τ1，τ2，…，τn）與最大可中斷負荷向量分別為［0.75，0.70，0.65，0.55，0.50，0.45，0.35］＄／（k W·h）與［70，70，80，85，65，55，75］MW。

給定差價合約電量在整個購電量中所占的比例γ為0.70，采用本文給出的競標策略進行仿真計算，實際利潤是基于概率性MCP預測結果取得的，理想利潤是假設準確無誤的預測到市場出清電價時取得的，1～12交易時段的利潤如表3所示，由表3可知，實際總利潤為98087＄；理想總利潤為100717＄；平均相對誤差為3.36%。

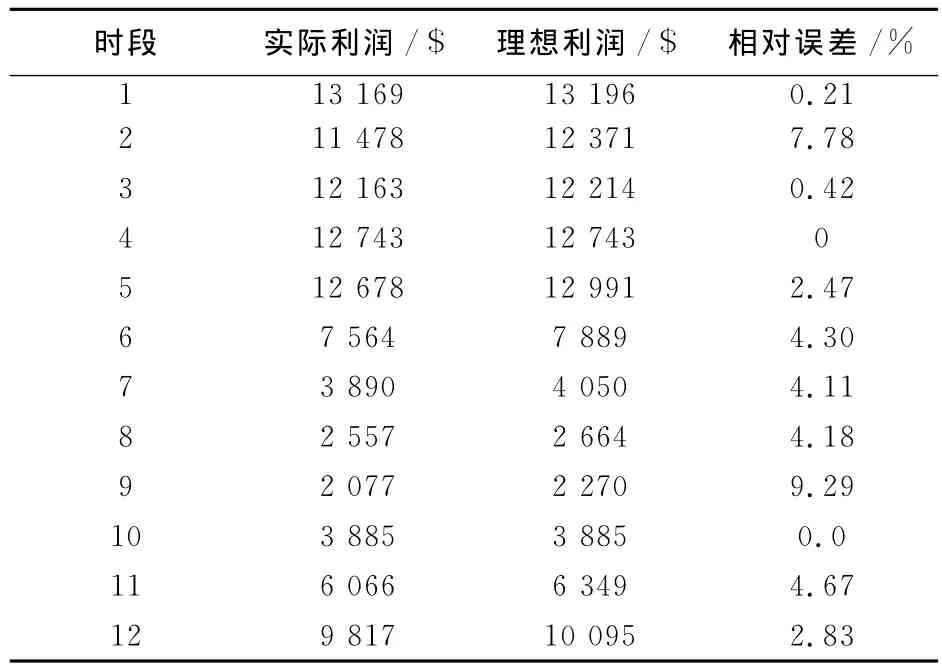
表3 供電公司各交易時段的利潤Tab.3 LSE＇s profit under each trading period

由表3可見，實際利潤與理想利潤的最大誤差為9.29%，最小相對誤差為0，平均相對誤差為3.36%，表明了本文給出的競標策略的有效性。

圖7 各交易時段電價曲線Fig.7 Price curve of all trading periods

在不同市場出清電價下中斷負荷的最大效益如圖9所示。由圖9可見，當市場出清電價為63.8＄／（MW·h）時，可中斷負荷的最優中斷量為75 MW，可中斷負荷帶來的效益為2160＄；當MCP增高到79.0＄／（MW·h）時，可中斷負荷的最優中斷量為130 MW，可中斷負荷帶來的效益為4650＄；當MCP進一步增高到91.6＄／（MW·h）時，可中斷負荷的最優中斷量為280 MW，可中斷負荷帶來的效益為12623＄。這表明供電公司擁有一定量的可中斷負荷，能夠為供電公司帶來可觀的經濟效益，提供了供電公司響應于批發市場購電電價的能力，有利于供電公司規避批發市場購電電價異常增高（price spike）時的購電決策風險。

當差價合約電量在整個購電量中所占的比例分別為0、0.70、0.90時，供電公司在第16交易時段的競標曲線如圖10所示。由圖10可見，差價合約電量在整個購電量中所占的比例越高，供電公司的競標段越少，供電公司在日前市場上的策略性競標行為減少，這是因為差價合約有保證供電公司購電量和規避風險的作用。

圖8 負荷預測曲線（情形2）Fig.8 Load forecasting curve under（case 2）

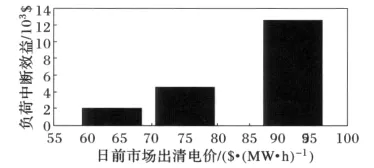
圖9 不同日前市場出清電價下中斷負荷的最大效益Fig.9 Profit of interrupt load under different MCP

圖10 不同差價合約購電量下的供電公司競標曲線Fig.10 LSE＇s bidding curve under different purchasing quantity at contract for difference

6 結論

（1）分時電價基本上反映了批發市場購電電價的波動，能夠引導電力資源在需求側的優化配置。

（2）市場出清電價越高，可中斷負荷的最優中斷量越多、發揮的作用越大，可中斷負荷有利于供電公司規避批發市場購電電價異常增高（price spike）時的購電決策風險。

（3）差價合約購電量的增加使得供電公司在日前市場上的策略性競標行為減少。

［1］ 文福拴，David A K（Wen Fushuan，David A K）.電力市場中的投標策略（Bidding strategies in electricity markets）［J］.電力系統自動化（Automation of Electric Power Systems），2000，24（14）：1－6.

［2］ 劉俊勇，劉瑞花，何邁（Liu Junyong，Liu Ruihua，He Mai）.以絕對離差為風險計量指標的購電分配模型（Electricity procurement optimal decision－mak－ing model of power supply company based on absolute deviation risk measurement）［J］.電力系統及其自動化學報（Proceedings of the CSU－EPSA），2007，21（5）：1－7.

［3］ 謝俊，陳星鶯，廖迎晨，等（Xie Jun，Chen Xingying，Liao Yingchen，et al）.基于機會約束規劃的供電公司最優報價策略（Optimal bidding strategies for distribution companies based on chance constrained programming）［J］.電力系統及其自動化學報（Proceedings of the CSU－EPSA），2007，19（2）：39－43.

［4］ 段登偉，劉俊勇，吳集光（Duan Dengwei，Liu Junyong，Wu Jiguang）.計及風險的配電公司最優分時零售電價模型（Optimal TOU retail pricing models for distribution utility with risk management）［J］.電力系統自動化（Automation of electric power systems），2005，29（3）：8－12.

［5］ Chen C S，Leu J T.Interruptible load control for Taiwan Power Company［J］.IEEE Trans on Power Systems，1990，5（2）：460－465.

［6］ 王秀麗，黃敏，陳天恩，等（Wang Xiuli，Huang Min，Chen Tianen，et al）.計及可靠性的電力市場分時定價方法（Power system hourly pricing methods considering reliability）［J］.電力系統自動化（Automation of Electric Power Systems），2009，33（10）：29－33.

［7］ Le Anh Tuan，Bhattacharya K.Competitive framework for procurement of interruptible load services［J］.IEEE Trans on Power Systems，2003，18（2）：889－897.

［8］ Fahrioglu M，Alvarado F L.Designing incentive compatible contracts for effective demand management［J］.IEEE Trans on Power Systems，2000，15（4）：1255－1260.

［9］ Rodriguez C P，Anders G J.Energy price forecasting in the Ontario competitive power system market［J］.IEEE Trans on Power Systems，2004，19（1）：366－374.

［10］Rodriguez C P，Anders G J.Bidding strategy design for different types of electric power market participants［J］.IEEE Trans on Power Systems，2004，19（2）：964－971.