改進的人工魚群算法設計次同步阻尼控制器

鄧盼盼，李興源，王渝紅，穆子龍，顧 威

（四川大學電氣信息學院，成都 610065）

與交流輸電相比，高壓直流輸電HVDC（high voltage direct current）具有高度可控、調節迅速、傳輸功率大、運行靈活等特點，在遠距離大容量輸電、區域電力系統互聯等方面有其優越性。目前，直流輸電因其在經濟和技術上的優勢，在遠距離大容量輸電和大區聯網兩個方面得到廣泛應用［1，2］。但是另一方面，HVDC系統的快速可控，存在著與汽輪發電機組軸系機械系統發生次同步扭振相互作用的可能性，這是一個需要重點關注的問題。

次同步振蕩SSO（subsynchronous oscillation）是指汽輪發電機組在運行平衡點受到擾動后處于特殊運行狀態下出現的一種異常狀態，在這種運行狀態下，電氣系統與汽輪發電機組之間在一個或多個低于系統同步的頻率下進行顯著的能量交換［3］。

在以往針對次同步振蕩的研究文獻中，通過各種方法設計控制器實現了對振蕩的抑制［4～6］。但一般方法設計出的控制器難以達到最好效果，且往往是針對某一運行情況，控制器參數固定。人工魚群算法AFSA（artificial fish swarm algorithm）擁有自學習、互學習能力，善于處理多維多目標問題，特別適用于非線性系統，并具有較好的魯棒性，但易陷入局部最優值。

本文通過對人工魚的覓食行為、聚群行為、追尾行為和行為選擇進行了分析、改進，使得AFSA算法得到改善。并基于此改進算法，以四川電網向家壩－上海直流輸電系統的送端為研究對象，設計了次同步阻尼控制器SSDC（subsynchronous damping controller），以達到抑制SSO的目的。

1 AFSA算法及其改進

1.1 AFSA算法

魚行動的特點就是自行或尾隨其他魚找到營養物質多的地方，因而魚生存數目最多的地方一般就是本水域中營養物質最多的地方［7］。AFSA算法就是根據這一特點，通過構造人工魚來模仿魚群的覓食、聚群及追尾行為，從而實現尋優［8］。

以求極小值問題為例，在一個n維的目標搜索空間中構造m條人工魚組成一個魚群，第條人工魚的位置可以用向量xi＝［xi1xi2… xin］表示，其在當前位置的食物濃度即適應度函數為Y＝f（x）。人工魚的感知距離即視野用V表示，人工魚在運動過程中感知其視野范圍內其他魚的狀況從而決定自己的行為選擇。擁擠度因子用δ描述，表示在某個位置附近的擁擠程度，取0＜δ＜1。人工魚的典型行為有覓食、追尾和聚群［9］，以下分別進行介紹。

1.1.1 追尾行為

設人工魚當前狀態為xi，探索視野范圍內的人工魚中Yi為最小的伙伴xj。如果xj的狀態具有較高的食物濃度并且其周圍不太擁擠，則朝伙伴xj的方向前進一步；否則執行覓食行為。

1.1.2 覓食行為

當前人工魚xi，在其視野范圍內隨機選擇一個狀態量xj，如果適應度函數Yj＜Yi，則向該方向前進一步，前進步長step的方向與向量xixj同向。反之，再重新隨機選擇狀態xj，判斷是否滿足前進條件；反復幾次后，如果仍不滿足前進條件，則隨機移動一步。

1.1.3 聚群行為

當前人工魚xi，探索當前視野內的伙伴數目nf及其中心位置xc，如果Yc／nf＞δYi，表明伙伴中心位置有較多的食物并且不太擁擠，則朝中心位置向前進一步。

在AFSA中，設置一個公告板，用以記錄當前所有人工魚中最佳狀態及該狀態的食物濃度。各人工魚每次行動完畢后，將最新位置的食物濃度與公告板中的食物濃度進行比較，如果該位置的食物濃度大于公告板中的食物濃度，則用該位置及其食物濃度代替公告板中的相應值。

1.2 改進AFSA算法

通過對AFSA算法的研究，發現視野范圍較大，人工魚的全局搜索能力強并快速收斂，但精度差；視野范圍較小，人工魚的局部搜索能力強，但易陷入局部最優值。步長大，收斂速度快，但有時會出現振蕩現象；步長小，收斂速度慢，但求解精度高。

根據AFSA算法的性質，調整視野V和步長step公式為

式中：T為當前迭代次數；Tmax為最大迭代次數。

如式（1）所示，應先使視野V和步長step有一較大初始值，以便于進行全局搜索。而隨著迭代次數的增加，應逐步減小V和step的值。在算法運行后期，逐步加強局部搜索，定位在最優解附近區域并進行精細搜索，從而在保證收斂速度的基礎上提高了算法的局部搜索能力和尋優結果的精度。

在覓食行為中，人工魚隨機選擇一個狀態，如果該狀態優于當前位置，沒有必要向該方向移動一步，為了加快搜索速度，人工魚可以直接移動到該位置。反復幾次后，如果仍不滿足前進條件，則原地不動，而不是隨機移動一步。另外，可以通過調控覓食行為中的重復嘗試次數，防止結果陷入局部極值。為限制盲目聚群，對nf的值做出限制：當前人工魚xi，探索當前視野內的伙伴數目，當nf＞2時，才進行是否聚群判斷。

整個算法的行為選擇順序可以調整為覓食、追尾、聚群。人工魚的初始狀態都是隨機的，首先嘗試覓食，可使每條人工魚均有較好的狀態后，再進行追尾和聚群。這樣避免了盲目的追尾、聚群行為，有效提高了算法的收斂速度。

2 系統模型

四川是一個電力輸出大省。根據2012年四川電網豐水期大方式規劃數據，四川電網全口徑裝機容量37357 MW。到2012年，川南將建成向家壩－上海和錦屏－蘇南兩回±800 k V特高壓直流輸電線路。其中向上直流送端換流站落點集中的交直流混合輸電系統穩定性問題成為亟待研究與解決的重點，其拓撲結構如圖1所示。

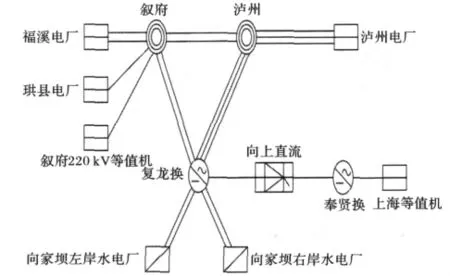
圖1 拓撲結構Fig.1 Topology structure

本文以PSCAD／EMTDC作為軟件平臺，建立如圖1所示的電磁暫態模型，研究各種孤島運行方式下，向上直流輸電系統與其送端臨近大型火電機組的次同步振蕩特性。根據仿真結果，向上直流降功率至20%的運行方式中，瀘州機組次同步振蕩情況比較嚴重，可能會對機組的軸系造成疲勞積累，縮短發電機軸系的壽命。

3 SSDC抑制SSO的原理

直流系統引起次同步振蕩的根本原因是其快速控制導致系統產生負阻尼。美國電力研究院EPRI（Electric Power Research Institute）首先提出了用SSDC來抑制直流系統次同步振蕩，其基本原理就是在次同步頻率范圍內為汽輪發電機提供合適的正阻尼。根據EPRI報告中SSDC的設計思路［10］，將SSDC裝設于直流系統的整流器控制側，然后通過經典控制理論中的超前、滯后校正補償在所需要頻率處的相位，可以有效增加系統次同步頻率段的電氣阻尼，從而抑制由直流輸電系統引起的次同步振蕩。如圖2所示，就是希望增加的SSDC回路能夠提供合適的阻尼轉矩，使電磁阻尼De為正值，以達到抑制次同步振蕩的目的。

對于次同步阻尼控制器的設計而言，輸入信號的選擇需要遵循兩個原則，一是可實現性，二是有效性［11］。為了實現本地可測量，及足夠的靈敏度，本文采用換流站高壓交流母線的頻率偏差信號ΔfHLZ，作為所設計的直流附加控制器SSDC的輸入信號。四階帶通濾波器的頻帶為5～45 Hz。慣性環節、相位校正環節以及比例增益環節中的參數K、T1、T2、T3為自適應參數，將利用改進的AFSA算法得到。

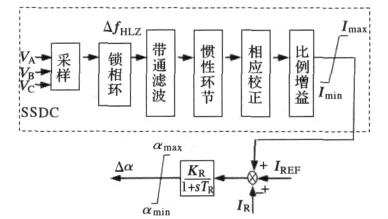
圖2 HVDC附加SSDC的基本原理Fig.2 Basic principle of HVDC added SSDC

4 基于改進的AFSA算法設計SSDC

4.1 設計思路

建立適應度函數前應先導出全系統的狀態方程。先確定多饋入直流與交流混合系統各元件的數學模型，包括機組發電機的轉子運動方程、軸系方程、勵磁繞組的電磁暫態方程、電力系統穩定器的方程、直流系統控制器的方程和直流輸電系統的方程，據此可得全系統狀態方程為

式中：X為狀態變量，X＝［ΔωiΔδiΔE′qΔEfΔV1ΔVSΔI1ΔISΔPdc］T；U為控制變量，U＝［ΔVISΔfHLZΔudc］T。ΔVIS、ΔV1、ΔVS分別為PSS控制器的輸入變量、中間量、輸出變量；ΔfHLZ、ΔI1、ΔIS分別為SSDC控制器的輸入變量、中間量、輸出變量；ΔPdc＝PdcREF－Pdc，PdcREF為直流功率的給定值，Δudc為直流功率的控制輸入信號。

安裝SSDC的目的是在復平面上讓次同步振蕩模式相應的特征根向左移動。系統特征值為

特征值的實部給出了系統阻尼，虛部給出了系統的振蕩頻率。負實部表示阻尼振蕩，正實部表示增幅振蕩。由此定義阻尼比

系統阻尼比確定了振蕩幅值的衰減速度。SSDC應針對機組不穩定的扭振頻率，使該振蕩模態的特征值實部最大限度地往復平面左移，即要求阻尼比越大越好。因此，要使次同步振蕩模態的阻尼比最大化，應將適應度函數選定為阻尼比。適應度函數為

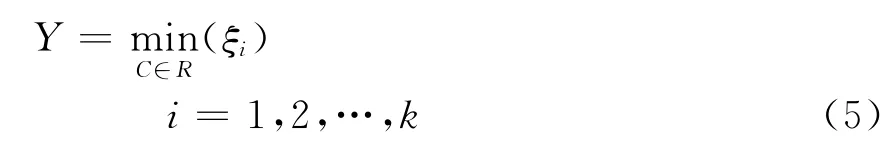
式中：ξi為第i個機電振蕩模態的阻尼比；C為系統的運行條件；R為所有可能運行條件的集合。

因此，利用改進的AFSA算法進行SSDC的設計，首先應通過選定的控制器自適應參數構造人工魚來模仿魚群的覓食、聚群及追尾等行為，以阻尼比作為適應度函數來比較各條人工魚的狀態，從而實現尋優。這樣SSDC的設計問題就轉化為阻尼比尋優的問題。

4.2 算法流程

步驟1 初始化人工魚群規模，將魚群的規模設定為m＝10，搜索空間維數定為N＝4，每一條人工魚的元素分別代表變量K、T1、T2、T3；初始化視野V和步長step、擁擠度δ、最大重復嘗試覓食次數trynumber、最大迭代次數等參數。

步驟2 按式（1）計算視野V和步長step。步驟3 每個個體依次進行覓食、追尾和聚群行為。

步驟4 根據每一條人工魚的當前狀態，即K、T1、T2、T3代入狀態方程，解出特征值，再將特征值代入適應度函數，計算出每條人工魚所對應的適應值，并將其適應值與公告板進行比較，若較好，則將其賦給公告板。

步驟5 檢查終止條件。（達到預定迭代次數或足夠好的適應值），如果滿足終止條件，則輸出最優解（公告板中人工魚狀態和函數值），算法終止；否則，轉入步驟2。

5 仿真分析

以次同步振蕩最嚴重的向上直流降功率至20%的運行方式為例，針對瀘州機組固有扭振頻率：13.6 Hz，25.6 Hz，30.7 Hz，首先采用Prony辨識瀘州機組的次同步振蕩模態。

表1 次同步振蕩模態Prony辨識分析Tab.1 Prony identification analysis for SSO modal

從表1中可以看出，有三個振蕩模態，其中模態1特征值實部接近于零，屬于不穩定狀態，系統在受到擾動后，容易激發次同步振蕩。

然后將采用遺傳算法GA（genetic algorithm）設計出的SSDC，以及采用改進AFSA算法得到的SSDC加到向上直流整流側控制系統中，對系統重新進行Prony辨識，結果如表2和表3所示。

表2 加入GA算法SSDC后次同步振蕩模態Prony辨識分析Tab.2 Prony identification analysis for SSO modal with SSDC of GA

表3 加入改進的AFSA算法SSDC后次同步振蕩模態Prony辨識分析Tab.3 Prony identification analysis for SSO modal with SSDC of improved AFSA

從表2與表3的對比中可以看出，加入了SSDC以后，各個模態下的特征值實部均往復平面左移，阻尼比也明顯增大。但是使用了改進的AFSA算法設計的SSDC與使用遺傳算法設計出的SSDC相比，能夠使各個模態下的特征值實部更大限度地往復平面左移，相應的阻尼比也更好。

同時，針對這一運行方式，采用時域仿真來驗證用GA算法設計出的SSDC，以及采用改進AFSA算法得到的SSDC對次同步振蕩的抑制作用。機組模型中均采用4質量塊的軸系模型，分別為高中壓缸（HIP）、低壓缸A（LPA）、低壓缸B（LPB）和發電機缸（GEN）。取故障為2 s時瀘州到復龍換流站，1回線單相接地故障，0.1 s后恢復。仿真結果如圖3～圖5所示。

由圖4和圖5可以看到，加入了SSDC以后，軸系的扭振均呈衰減趨勢。但是使用了改進的AFSA算法的SSDC比使用遺傳算法設計出的SSDC能在更短的時間內使扭矩衰減至穩定值，使得系統能夠更快進入穩定運行狀態，同時也保證了汽輪發電機組軸系的安全。并且在加裝針對瀘州機組設計的SSDC后，對福溪、珙縣機組的扭振相互作用現象，也有一定的抑制作用，如圖6和圖7所示。

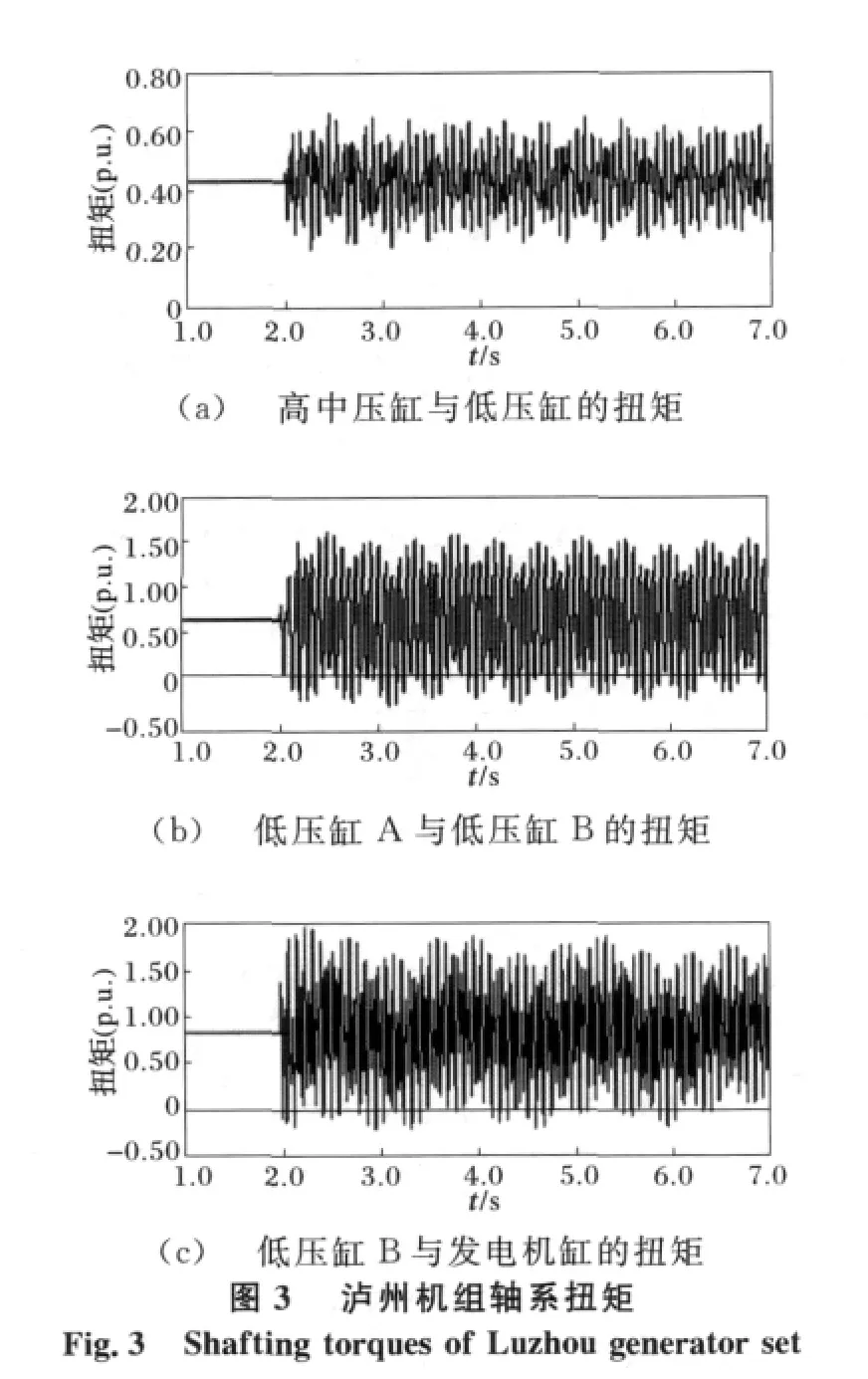
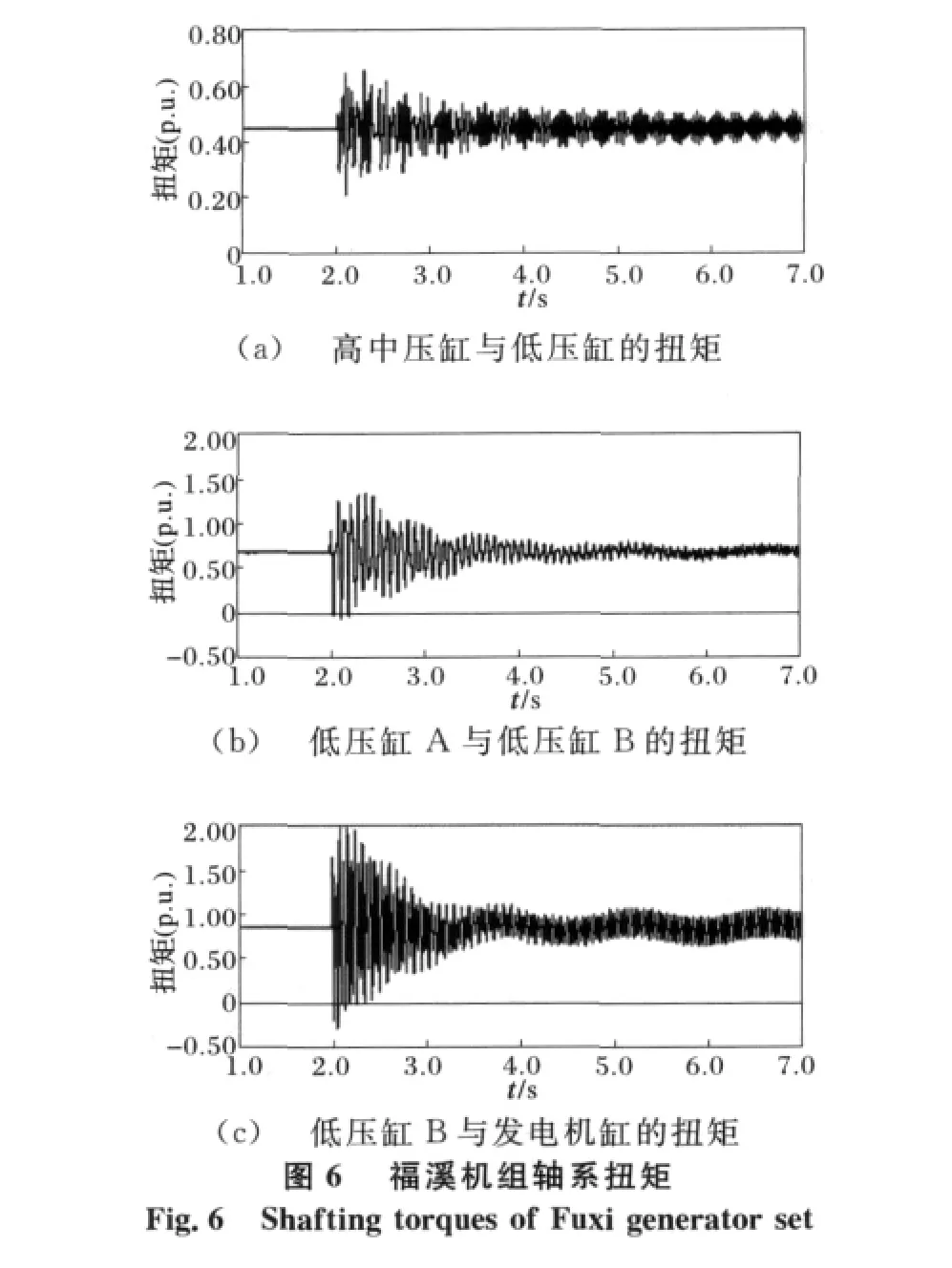
圖7 珙縣機組軸系扭矩Fig.7 Shafting torques of Gongxian generator set

6 結語

本文提出的改進AFSA算法較好地平衡了全局搜索能力和局部搜索能力，收斂迅速且不易陷入局部最優值，提高了該算法的自適應能力和優化精度。基于改進的AFSA算法，進行了次同步阻尼控制器的設計。通過Prony辨識分析和PSCAD／EMTDC的電磁暫態仿真證明了該次同步阻尼控制器能有效抑制軸系扭振，且具有時間短、具有一定魯棒性的特點。

［1］ 李興源.高壓直流輸電系統的運行［M］.北京：科學出版社，1998.

［2］ 浙江大學發電教研組直流輸電科研組.直流輸電［M］.北京：電力工業出版社，1982.

［3］ 程時杰，曹一家，江全元.電力系統次同步振蕩的理論與方法［M］.北京：科學出版社，2009.

［4］ 伍凌云，李興源，龔勛，等（Wu Lingyun，Li Xingyuan，Gong Xun，et al）.基于模糊免疫方法的次同步阻尼控制器設計（Design of subsynchronous damping controller based on fuzzy immune method）［J］.電力系統自動化（Automation of Electric Power Systems），2007，31（11）：12－16.

［5］ 劉振亞.特高壓直流輸電技術研究成果專輯（2005年）［M］.北京：中國電力出版社，2006.

［6］ Svensson S，Mortensen K.Damping of subsynchronous oscillations by an HVDC link an HVDC simulator study［J］.IEEE Trans on Power Apparatus and Systems，1981，100（3）：1431－1439.

［7］ 班曉娟，艾冬梅，陳泓娟，等.人工魚［M］.北京：科學出版社，2007.

［8］ 李曉磊，邵之江，錢積新（Li Xiaolei，Shao Zhijiang，Qian Jixin）.一種基于動物自治體的尋優模式：魚群算法（An optimizing method based on autonomous animals：fish－swarm algorithm）［J］.系統工程理論與實踐（Systems Engineering Theory ＆Practice），2002，22（11）：32－38.

［9］ 李曉磊，馮少輝，錢積新，等（Li Xiaolei，Feng Shaohui，Qian Jixin，et al）.基于人工魚群算法的魯棒PID控制器參數整定方法研究（Parameter tuning method of robust PID controller based on artificial fish school algorithm）［J］.信息與控制（Information and Control），2004，33（1）：112－115.

［10］Piwko R J，Larsen E V.HVDC system control for damping of subsynchronous oscillations［J］.IEEE Trans on Power Apparatus and Systems，1982，101（7）：2203－2211.

［11］周鐵強，劉福生（Zhou Tieqiang，Liu Fusheng）.高壓直流輸電系統次同步振蕩的幾種研究方法及其對比分析（HVDC system subsynchronous resonance several researching method and comparing analysis）［J］.電力系統及其自動化學報（Proceedings of the CSUEPSA），1992，4（2）：32－40.