恒化器中一類具有非常數消耗率微生物培養模型的定性分析

凌志超， 張天四

（上海理工大學理學院，上海 200093）

恒化器是一種用來連續培養微生物的實驗室儀器，其營養物的輸入和流出近似地模擬了自然界的連續代謝過程，主要用于模擬湖泊和海洋中單細胞藻類浮游生物的生長，在廢水處理或者基因產品生產等領域具有重要應用，很多學者對此進行了大量的研究［1－7］.如文獻［5］討論了微生物連續培養三維競爭模型系統解的穩定性.文獻［6］對消耗率參數為一次函數的單食物鏈模型進行了定性研究.而文獻［7］則研究了具有正比增長率且消耗率參數分別為一次函數和二次函數時的二維微生物培養模型系統的極限環和Hopf分支存在性.

本文主要考慮三維單食物鏈種群競爭模型，假設被捕食種群對營養基和捕食種群對被捕食種群具有形為δ（s）＝A＋Bs＋Cs2的二次函數消耗率參數，并通過定性分析證明系統平衡點的存在性和穩定性，以及系統正向不變集的存在性.

1 變消耗率模型及定性分析

考查恒化器中只有兩種微生物，即捕食和被捕食種群的三維單食物鏈模型

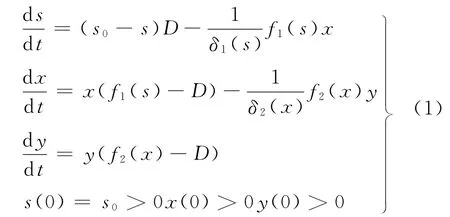
式中，s（t），x（t），y（t）分別表示t時刻恒化器中營養基、被捕食種群和捕食種群的質量分數；s0為輸入營養基的質量分數；D為輸入輸出率；δ－11（s），δ－12（s）分別為被捕食種群x對營養基s的消耗率和捕食種群y對被捕食種群x的消耗率，δ－11（s）＝分別為被捕食種群x和捕食種群y的生長函數，ki為系數，均為正常數，i＝1，2.

s（t）不會比初始流入的質量分數s0更大，從而0＜s≤1.

證明 由系統（2）的第2和第3個方程知，若mi≤1（i＝1，2），則若mi＞1且λi≥1時（i＝1，2），也有所以，當t→∞時，x（t）→0，y（t）→0.

命題說明，當微生物種群x，y本身的參數，即最大增長率mi≤1較小時或mi＞1較大但半飽和常數ki≥（mi－1）也較大時，微生物種群都不能存活，就失去了研究的價值，因此，在下面的討論中，均假設mi＞1，λi＜1，i＝1，2.

考慮系統（2）的平衡解，其必滿足方程組

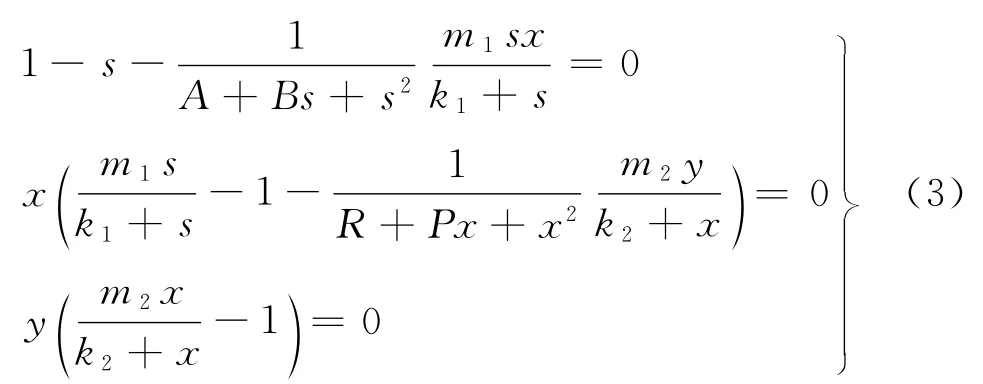
解方程組得平衡點E0（1，0，0），E1（λ1，（1－λ1）（A＋Bλ1＋λ21），0），Ec（sc，xc，yc）.其中，xc＝λ2＞0，sc，yc滿足方程

記

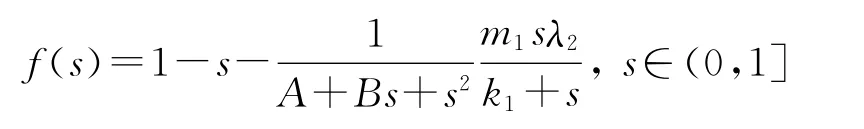
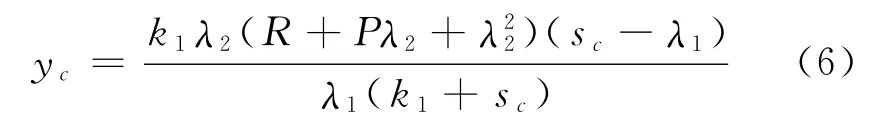
定理1 系統（2）存在E0（1，0，0），E1（λ1，（1－ λ1）（A＋Bλ1＋λ12），0），Ec（sc，xc，yc）這3個有限遠的平衡點，其中，E0為鞍點，不穩定.

當（1－λ1）（A＋Bλ1＋λ21）＞λ2或（1－λ1）（A＋Bλ1＋λ21）＜λ2，且

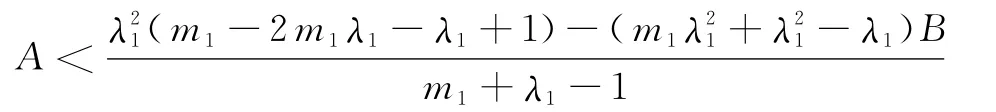
時，E1為不穩定平衡點.

當（1－λ1）（A＋Bλ1＋λ21）＜λ2，且

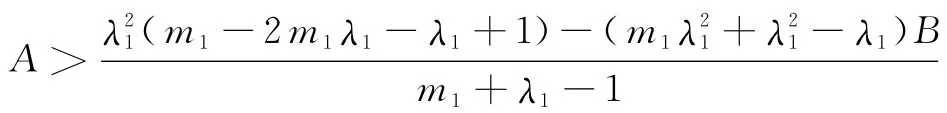
時，E1為穩定平衡點.

證明 系統（2）在E0處的線性化矩陣為

對應的特征方程的特征根為γ1，2＝－1＜0，由于上面假設λi＜1，i＝1，2.可推知

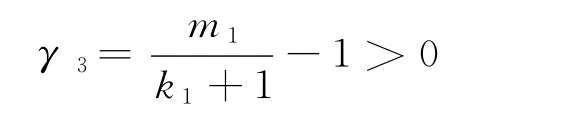
所以，E0為鞍點，不穩定.

在E1處，特征方程為

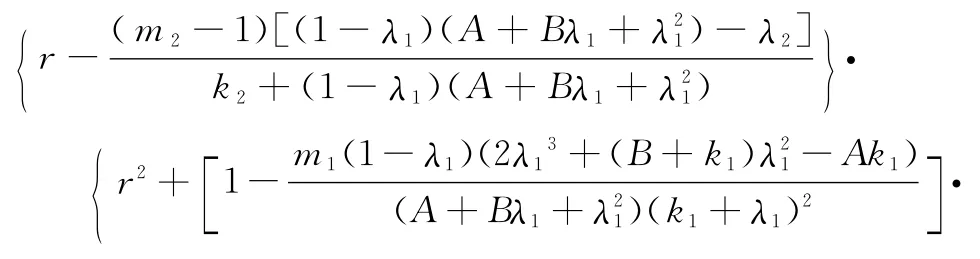
特征根

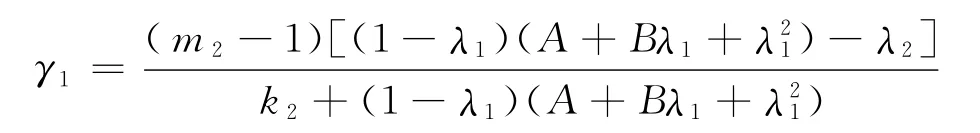
當

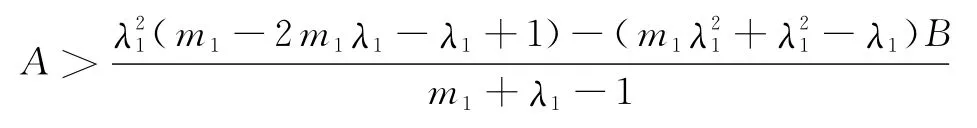
時，b＞0，所以，r2，r3均有負實部或均為負實根，從而E1是穩定的.

而當

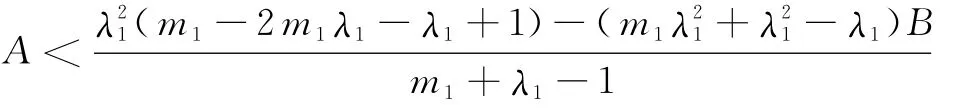
時，b＜0，此時，r2，r3均有正實部或均為正實根，從而E1為不穩定的平衡點.

在Ec處，其對應的特征方程為r3＋a1r2＋a2r＋a3＝0，其中

定理2 系統（2）存在正向不變集

其中，0＜N＜∞，θ0∈R＋.

證明 系統（2）存在解平面x＝0，y＝0，考察平面s＝0，由于所以，系統（2）軌線當t增加時是由區域Ω1＝｛（s，x，y）｜s＜0，x＞0，y＞0｝穿過平面s＝0而進入區域Ω，即從任意（s，x，y）出發的軌線，當t→∞時穿過平面s＝0而進入Ω.再考慮平面

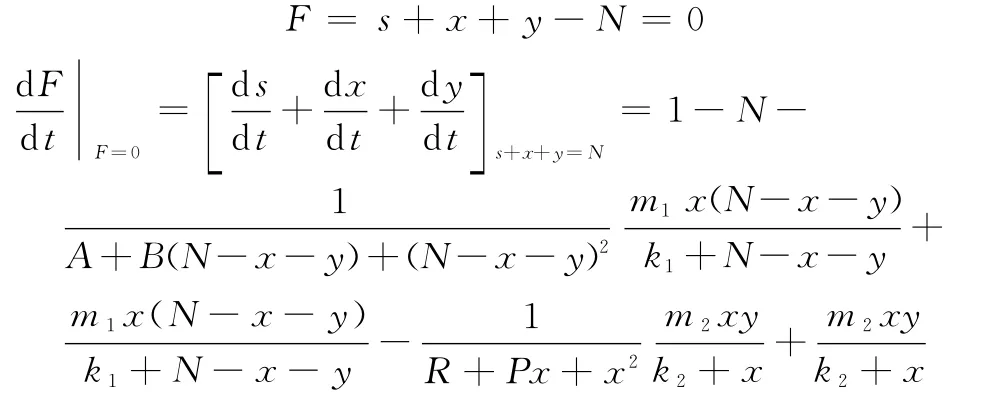
因為x，y有界，A，B，C，R，P，Q，mi，ki均為常數，i＝1，2.所以，對充分大的N，有則系統（2）的軌線穿過平面F＝0時，是由外向內進入區域Ω的，即任意從（s，x，y）出發的軌線，當t→∞時，不會穿過F＝0跑出區域Ω.

綜上所述，Ω為系統（2）的不變區域.

2 結束語

研究了一類變消耗率食物鏈模型，分析了其平衡點的類型，證明了各個平衡點的穩定性，并證明出系統存在正向不變集，由此可見，對于此類模型，當參數滿足一定條件時，同時培養兩種微生物且使微生物種群共存這一目的是可以實現的.

［1］ Li Bingtuan.Simple food chain in a chemostat with distinct removal rates［J］.J Math Anal Appl，2000，242（1）：75－92.

［2］ Pilyugin S S，Waltman P.Multiple limit cycles in the chemostat with variable yield［J］.Math Biosci，2003，182（2）：151－166.

［3］ Nelson M I，Sidhu H S.Analysis of a chemostat model with variable yield coefficient：Tessier kinetics［J］.J Math Chem，2005，38（4）：605－615.

［4］ 宋國華，朱榮升.具有內代謝的微生物連續培養數學模型及解的全局穩定性［J］.生物數學學報，1996，11（4）：27－30.

［5］ Zhu Lemin.Limit cycles in chemostat with constant yields［J］.Math Comp Mode，2007，45（7／8）：927－932.

［6］ 劉婧，楊淑芹.恒化器中微生物連續培養單食物鏈模型的定性分析［J］.大連海事大學學報，2004，30（3）：88－91.

［7］ 鐘鎮權.具有變消耗率微生物連續培養模型的定性分析［J］.生物數學學報，2007，22（3）：447－454.

［8］ 馬知恩，周義倉.常微分方程定性與穩定性方法［M］.北京：科學出版社，2001.