一類耦合KdV方程的孤波解和周期波解及其相互關系

張衛國， 徐 偉， 李 想

（上海理工大學理學院，上海 200093）

1 問題的提出

耦合KdV波動方程［1］

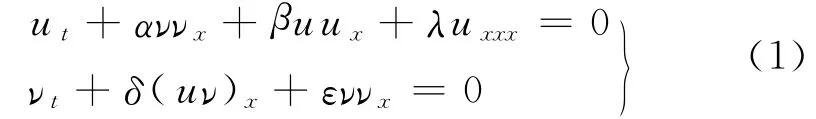
可用來描述兩個內部長波之間相互作用的過程，其中α，β，λ，δ，ε為非零參數.在變量ν＝0時，方程（1）可約化為在固態物理、等離子物理、流體物理和量子理論等領域有廣泛應用的KdV方程［2－7］.

近年來，多位學者研究了方程（1）的孤波解求解問題.陸寶群等分別利用待定系數法和函數展開法求得了方程（1）的精確孤波解［8－9］；Ito［10］運用循環算子推出了當α＝δ＝－2，β＝－6，ε＝0時，耦合方程

具有無限多的對稱性；葉彩兒［11］證明了當α＝β＝λ＝δ＝ε＝1時，耦合方程

具有Painleve性質，在Painleve性質下可積，并通過自Backlund變換求出了方程（3）的孤立波解和奇異行波解.

然而以往文獻沒有給出過方程（1）孤波解唯一性的結論，也沒有研究過方程（1）的孤波解與周期波解之間的關系.現運用平面動力系統方法研究耦合KdV波動方程（1）的孤波解、周期波解的存在性，給出孤波解唯一性的結論，并分別運用假設待定法和首次積分法求出這兩種解的精確解，還進一步研究這兩種解的相關性.目前研究非線性發展方程孤波解與周期波解之間相互關系的文獻還比較少，這種研究在理論和應用上顯然是有意義的，因為它可揭示參數的變化對解的影響，加深人們對非線性波動的認識，并給非線性波動的控制提供有益的信息.

文中首先運用平面動力系統理論和方法對方程（1）的行波解進行定性分析，給出不同參數下的全局相圖，說明在一定條件下該方程只存在唯一的鐘狀孤波解，而同時卻有無窮多個周期波解.其次分別運用待定系數法和首次積分法求出該方程鐘狀孤波解和周期波解的精確表達式，并直觀指出它們所對應的解軌線在全局相圖中的位置.隨后討論了方程孤波解與Jacobi橢圓函數型周期波解的關系，即當模數k趨近于1時，Jacobi橢圓函數周期波解逐漸擴張演變為鐘狀孤波解.最后作出了Jacobi橢圓函數周期波解向鐘狀孤波解演變的三維示意圖.

2 方程（1）有界行波解的定性分析

設方程（1）有行波解u（x，t）＝u（ξ）＝u（x－ct），ν（x，t）＝ν（ξ）＝ν（x－ct），將其代入方程（1）中，可得

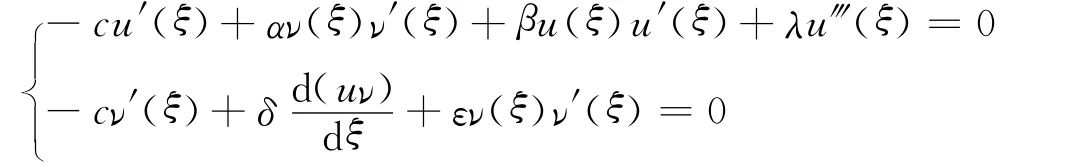
將上式積分一次，可得

其中，E1，E2為積分常數.由式（4）中第二個式子，可知

為使得u（ξ）處處正則，現取E2＝0，這等價于u（ξ），ν（ξ）當的極限滿足

將式（6）代入式（4）中第一個式子，可得

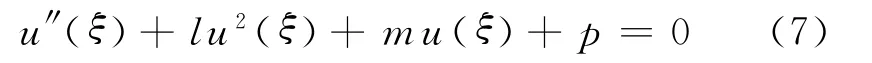
其中

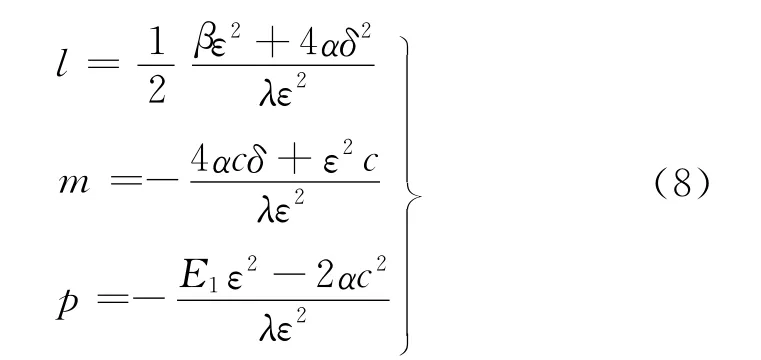
這樣，在積分常數E2＝0的條件下就將求方程（1）孤波解和周期波解的問題轉化為了式（6）和式（7）.由于式（6）中u（ξ）滿足方程（7），故對方程（7）解的性態和求解的研究是本文的關鍵.現在研究方程（7），令x＝u（ξ），y＝u′（ξ），則方程（7）可轉化為與之等價的平面動力系統

在（x，y）平面上，系統（9）有限遠奇點的個數依賴于方程f（x）＝lx2＋mx＋p＝0的實根的個數.記f（x）＝0的判別式為Δ＝m2－4lp.易知該方程在Δ＝0時有一個實根，在Δ＜0有兩個共軛復根，在Δ＞0有兩個不等的實根.因現只考慮系統（9）的有界行波解，所以始終假設Δ＞0.設方程f（x）＝0的實根為a1，a2，分別為當l＞0時，a1＜a2；當l＜0時，a1＞a2.記系統（9）在奇點Pi（ai，0）（i＝1，2）處的Jacobi矩陣為

顯然，系統（9）是Hamilton系統，有首次積分

由Liouville定理的推論可知，Hamilton系統不可能存在漸近穩定與不穩定的平衡點（焦點、結點），平衡點只能是中心或鞍點；也不可能存在漸近穩定與不穩定的極限環，只可能存在簡單閉軌.在典型的Hamilton系統中，只可能存在有限個平衡點，但可以有無窮多個周期閉軌.

對系統（9）作Poincare變換，可得系統（9）在y軸上各存在一對無窮遠奇點Ai（i＝1，2），且在Ai周圍各存在一個拋物型區域.另外，Poincare圓盤的圓周為軌線.

由上述分析，可得到系統（9）的全局相圖，如圖1所示.

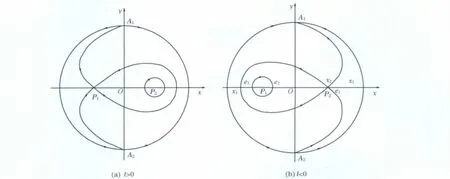
圖1 系統（9）的全局相圖Fig.1 Global phase portraits of system（9）

由相圖1，可得到下列命題.

命題1 設l≠0，除去奇點P1，P2和軌線L（P1，P1）以及由L（P1，P1）包圍的閉軌線外，系統（9）的其它軌線均是無界的，并且這些軌線上的點的x坐標值和y坐標值也均是無界的.

證明 設l≠0，除去奇點P1，P2和軌線L（P1，P1），L（P2，P2）以及這些軌線周圍的閉軌線外，系統（9）的其它軌線均是無界的，它們在＋∞時，或者趨于A1或者趨于A2.因此，這些軌線上的y坐標值一定是無界的.下面用反證法證明這些軌線上的x坐標值也是無界的.設這些軌線上的點的x坐標值是有界的.一方面，由于軌線上的任意點的切線斜率滿足

命題2 設l≠0，系統（9）存在一條同宿軌道和無窮多條閉軌線（見圖1）.

考慮到平面動力系統（9）中的同宿軌對應方程（1）的鐘狀孤波解，閉軌對應方程（1）周期行波解，因此由命題1、命題2和全局相圖1，可得如下定理.

定理1 設積分常數E2＝0，若行波波速c和積分常數E1滿足m2－4lp＞0，則方程（1）存在唯一的鐘狀孤波解（對應于同宿軌道L（P1，P1））和無窮多個周期行波解.

由于所討論的方程（1）中參數α，β，λ，δ，ε都是非零的，故命題1和命題2中假設l≠0自然成立.

3 方程（1）的鐘狀孤波解

受文獻［12］的啟發，方程（7）有解

其中，A，B，s，D待定.將式（11）代入方程（7）中，根據es（ξ＋ξ0）（s＝0，1，2，3，4，5，6）的線性無關性，并經化簡得到A，B，s，D滿足的方程組

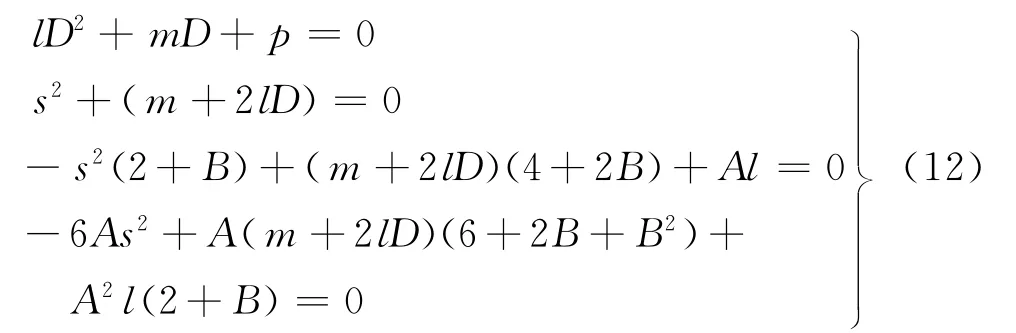
解方程組（12），可得下列兩組解

又因將式（14）中各數值代入式（11），可得方程（7）的解為

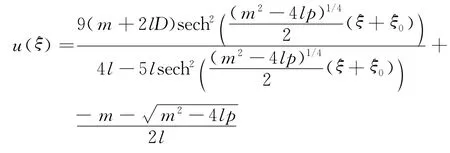
經判定，此解不是有界行波解，故可將其排除.

綜合上面計算和前面的定性分析的結果，可得到下面關于方程（1）鐘狀孤波解的定理.

定理2 假設定理1中條件成立，則方程（1）的唯一鐘狀孤波解為

其中，l，m，p由式（8）給定.孤波解（u（ξ），ν（ξ））中的u（ξ）對應于圖1中的同宿軌L（P1，P1）.

定理2中的唯一性，已由定理1給出.另外因為sechx是偶函數，當時的解與k＝時的解相同.

易驗，本文所求孤波解與文獻［8］用函數展開法所求方程（1）的鐘狀孤波解是等價的.文獻［9］用待定系數法所求鐘狀孤波解是本文所研究方程（1）的鐘狀孤波解式（15）和式（16）在m2－4lp＝16，E1＝E2＝0時的情況.文獻［10］中通過自Backlund變換求得方程（3）的孤波解是本文研究的方程（1）在α＝1，β＝1，λ＝1，δ＝1，ε＝1，即l＝5／2，m＝－5c時的特殊情況.用定性分析及假設待定結合方法的好處在于：利用定性分析的結果，可以清楚地看出方程（1）有界行波解存在的個數和大致形態，可以很直觀地指出用假設待定方法求出的方程（1）的有界行波解對應的解軌線在全局相圖中的位置，兩者之間具有一一對應的關系.

4 方程（1）的周期波解

現結合前面定性分析中的部分結論，通過適當變換并運用首次積分方法對方程（1）的周期波解進行求解.

由對方程（1）有界行波解的定性分析中可知，平面動力系統（9）是Hamilton系統，且具有首次積分式（10），式（10）即為系統（9）的Hamilton函數.以l＜0的情形為例，求出對應圖1（b）中同宿軌道所圍中心的閉軌線對應的周期波解，對于l＞0情形的結論可類似得到.

設（a，0）為周期軌道與x軸的交點，由于在對稱同宿軌道內包圍中心的同一周期軌道上點的Hamilton量相等，即于是，有

可證得Hamilton量的取值范圍為

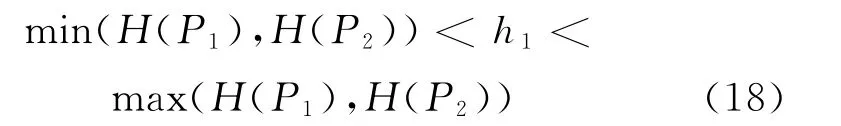
其中

由式（17），可得

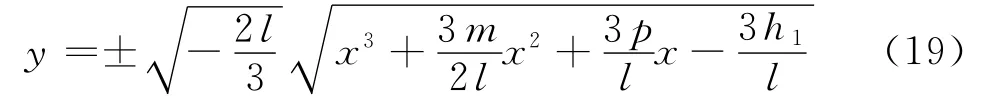
對上式積分一次，可得

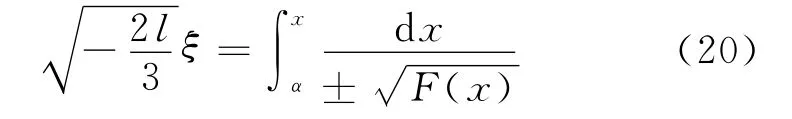
易驗，在Δ＝m2－4lp＞0和h1滿足式（17）條件下，F（x）＝0有3個實根e1，e2，e3，它們由l，m，p，h1確定，故F（x）可寫成F（x）＝（x－e1）（x－e2）（x－e3）.當l＜0時，有e3＜a2＜e2＜a1＜e1，且在（e3，e2）及（e1，＋∞）時，F（x）＞0，此時為求出有界的周期波解，應限制x在（e3，e2）內取值，如圖2所示.現取α＝e3，并令

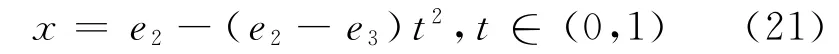
將式（22）代入式（20），可得

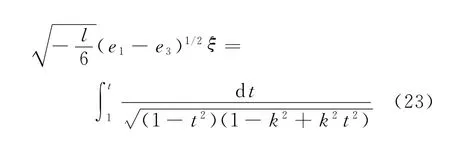
圖2 F（x）＞0的范圍Fig.2 Range of F（x）＞0

利用橢圓函數cn（ζ，k）的微分公式

令t＝cn（ζ），則式（24）變為

考慮到cn（0）＝1，由式（25），有

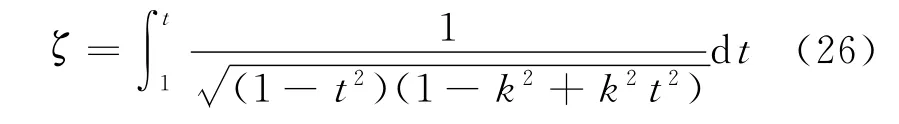
將式（26）代入式（23）中，立即有

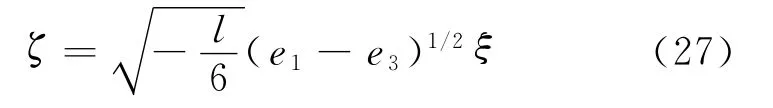
將其代入式（22），得到方程（7）的周期波解

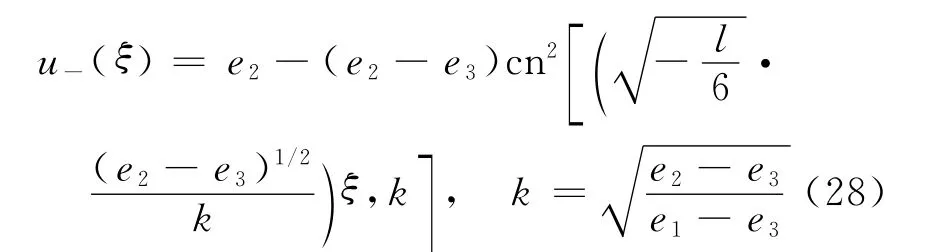
同理，當l＞0時，圖1（a）中同宿軌道所圍中心的閉軌線對應方程（7）的周期波解為

綜合上面的計算，可得到關于方程（1）的周期波解的如下定理.

定理3 設定理1中條件成立.則方程（1）有Jacobi橢圓函數周期波解

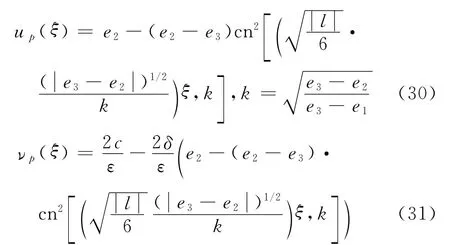
up（ξ）對應于圖1（a），（b）中的同宿軌道L（P1，P1）所包圍中心奇點的閉軌線.

下面通過假設待定法求方程（7）的周期波解.受文獻［13］的啟發，假設方程（7）有解

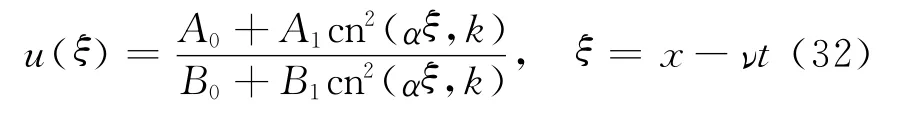
將其代入到式（7）中，可求得

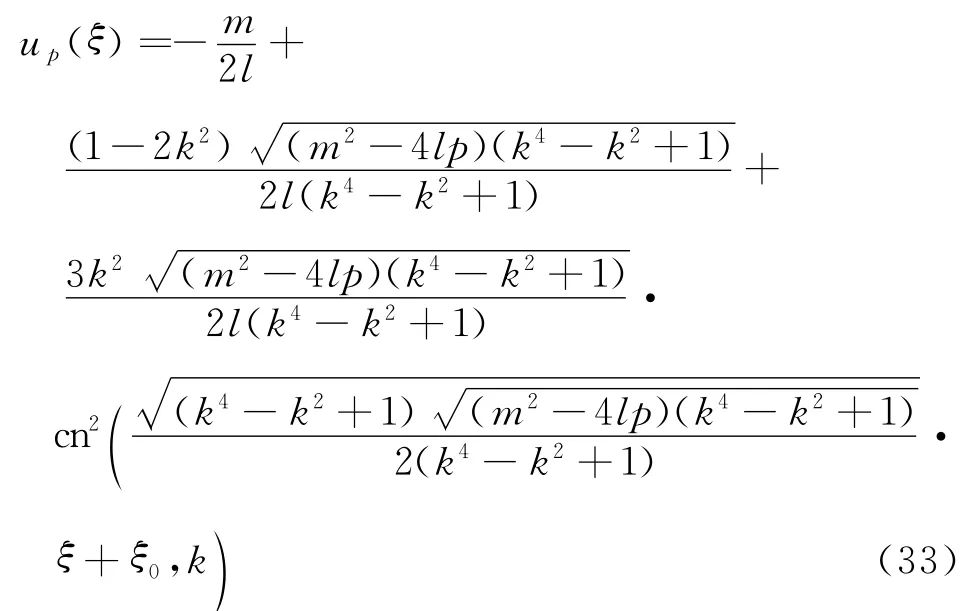
用首次積分法求解方程（1）的周期波解，主要目的在于以此說明橢圓函數中的模數k與周期波解對應的軌線和x軸的交點e1，e2，e3相關，從而k與方程（1）中的參數及波速等相關.

5 方程（1）的孤波解和周期波解的關系

從全局相圖的角度觀察，方程（1）的孤波解（u（ξ），ν（ξ））中的u（ξ）對應于全局相圖1（a），（b）中的同宿軌線L（P1，P1），而周期波解（up（ξ），νp（ξ））中的up（ξ）對應于包圍中心的閉軌線，它被包含于由同宿軌線L（P1，P1）所包圍的區域中.下面以l＜0的情形為例進行討論.考察在對稱同宿軌道內的周期波解up（ξ）當k→1時向孤波解u（ξ）的演變，對于l＞0情形的結論可類似得到.

當l＜0時，系統（9）過鞍點P1（a1，0）的同宿軌道上點的Hamilton量為其中再由Hamilton函數知，H即

Hamilton量為h2的軌線在l＜0時與x軸的交點.其中，包含于同宿軌道的周期閉軌線與x軸的交點的橫坐標e1，e2，e3與x1，x2，x3關系為x1＜e3＜e2＜x2＝a1＜e1＜x3（見圖1（b）），且當模數時，有e3→x1， e2→x2＝a1， e1→x2＝a1.

結合上面的分析，可求得

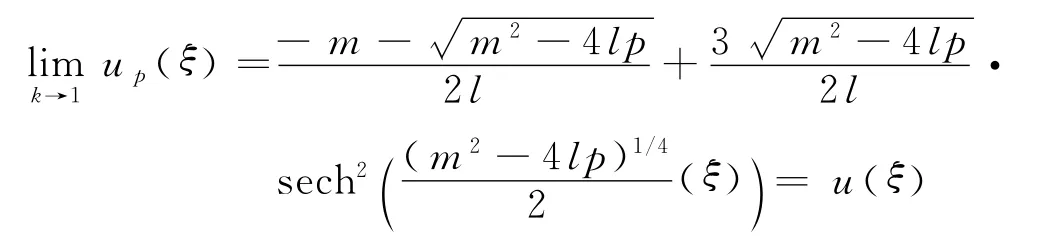
綜合上面的計算和前面的定性分析，可得到如下定理.

定理4 當k→1時，方程（1）的周期波解對應相圖上的周期閉軌擴張成同宿軌道L（P1，P1）.

為了直觀地體現周期波解與孤波解之間的關聯性，現作出Jacobi橢圓函數周期波解up（ξ）向孤波解u（ξ）演變的三維示意圖，如圖3所示.圖3中，取此時l＝3，m＝4，p＝1.

［1］ Kumpershmidt B A.A coupled Korteweg－de Vries equation with dispersion［J］.J Phys A：Math Gen，1985，（18）：571－573.

［2］ Garder C S.The Korteweg－de Vries equation and generalizations IV［J］.Journal of Mathematical Physics，1971，12（4）：1548－1551.

［3］ Konno K，Ichikawa Y H.A modified Korteweg－de Vries equation for ion acoustic waves［J］.J Phys Soc Japan， 1974，37（7）：1631－1636.

圖3 k→1時周期波解up（ξ）趨向于孤波解u（ξ）Fig.3 Periodic wave solution up（ξ）tends to solitary wave solution u（ξ）when k→1

［4］ Dodd R K，Eilbeckj C，Gibbon D J，et al.Solitons and nonlinear wave equations［M］.London：Academic Press Inc Ltd，1982.

［5］ Narayanamurti V，Varma C M.Nonlinear propagation of heat pulses in solids［J］.Phys Rev Lett，1970，25（16）：1105－1108.

［6］ Tappert F D，Varma C M.Asymptotic theory of selftrapping of heat pulses in solids［J］.Phys Rev Lett，1970，25（16）：1108－1111.

［7］ Zhang W G，Chang Q S，Fan E G.Methods of judging shape of solitary wave and solutions formula for some evolution equations with nonlinear terms of high order［J］.J Math And Appl，2003，287（1）：1－18.

［8］ Lu B Q，Pan Z L，Qu B Z，et al.Solitary wave solutions for some systems of coupled nonlinear equations［J］.Physics Letters A，1993，180（1）：61－64.

［9］ Xu X J，Zhang J F.New exact and explicit solitary wave solutions to a class of coupled nonlinear equations［J］.Communications in Nonlinear Science ＆Numerical Simulation，1998，3（3）：189－193.

［10］ Ito M.Symmetries and conservation laws of a coupled nonlinear wave equation［J］.Phys lett A，1982，91（7）：335－338.

［11］ 葉彩兒.幾個非線性發展方程（組）的精確解與Painleve分析［D］.杭州：浙江大學，2003：28－31.

［12］ 張衛國，劉剛，任迎春.非線性波動方程的孤波解與余弦周期波解［J］.上海理工大學學報，2008，30（1）：15－21.

［13］ An J Y，Zhang W G.Exact periodic solutions to generalized BBM equation and relevant conclusions［J］.Acta Mathematicae Applicatae Sinica，2006，22（3）：509－516.