層狀粘彈性地基一維固結特性

劉加才，馬 強

（南京工業大學 交通學院，南京210009）

地基的固結問題一直是工程界和理論界關心的熱點問題之一。Terzaghi最早提出一維固結理論，為固結理論的發展奠定了基礎。近年來一維固結理論有了較大發展，可以考慮較為復雜的情況，如加載隨時間變化［1］、滲透力對土體固結的影響［2］、土體非飽和［3］、有限應變［4］、土體材料非線性［5］、非達西滲流［6］。軟粘土具有粘彈性，地基土層通常具有成層性。一些學者將Terzaghi固結理論推廣到成層地基情況，如 Xie等［7］、Lee等［8］。另外一些學者考慮土體的黏滯性，研究了土體的一維固結問題，如趙維炳［9］、Hawlader等［10］、Li等［11］、Xie等［12］。由于問題的復雜性，同時考慮土體的成層性和黏滯性的文獻并不多見。Cai等［13］基于Kelvin流變模型，運用Laplace變換、矩陣傳遞法以及Laplace變換求解了任意荷載下成層粘彈性地基一維變形問題。Kelvin流變模型可以反映彈性后效，卻不能反映應力松弛。為了全面反映土體的粘彈性質，劉加才等［14］提出了基于廣義Voigt流變模型的雙層黏彈性地基求解方法，但求解過程較為復雜，不利于工程應用。本文采用巖土工程中應用較廣的Merchant流變模型，提出了層狀黏彈性地基的一維固結有限元分析方法，并對其固結特性進行了研究。

1 問題描述

1.1 計算簡圖

層狀粘彈性地基的一維固結問題如圖1所示。滿足如下基本假定：1）地基土層完全飽和；2）孔隙水和固體顆粒均不可壓縮；3）土體滲流滿足Darcy定律；4）壓縮和滲流僅發生在豎直方向；5）荷載為均布荷載，且瞬時施加；6）地基頂部為排水面，底部為不透水面；7）土體的粘彈性可采用 Merchant流變模型。圖中，E0i，E1i，η1i，為第i土層的 Merchant流變模型參數，kvi為第i土層的豎直向滲透系數。深度方向z坐標向下為正，坐標原點為第一層土體頂面。第i土層底面深度為hi。

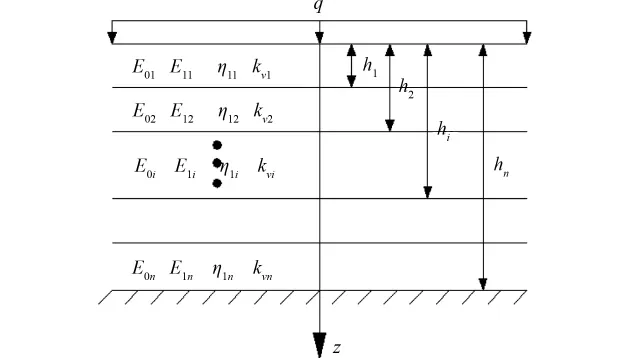
圖1 層狀黏彈性地基一維固結簡圖

對于任一土層，滿足控制方程式（1）［9，14］。

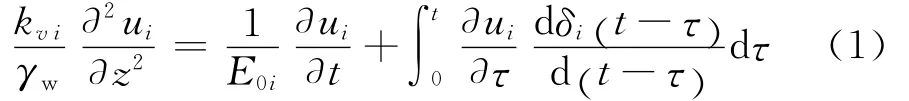
式中：i＝1，2，…，n為土層編號；ui為第i土層的超靜孔壓；δi為第i土層的Merchant流變模型柔度函數，如式（2）所示。

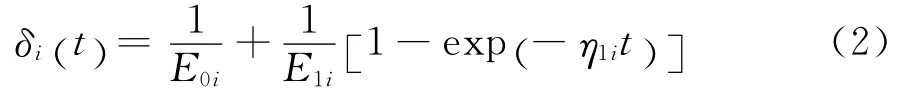
1.2 初始條件

由于荷載為均布荷載，且瞬時施加，任一深度處孔壓初始時刻均為q，如式（3）所示。

1.3 邊界條件

地基頂面排水，底面不透水，如式（4）、（5）所示：

2 有限元求解及解答有效性驗證

2.1 有限元求解

將地基沿固結方向劃分為若干2節點單元，節點作為每個單元的邊界，土層的分界線作為單元的節點。孔壓在單元上線性變化，可用式（6）表示。

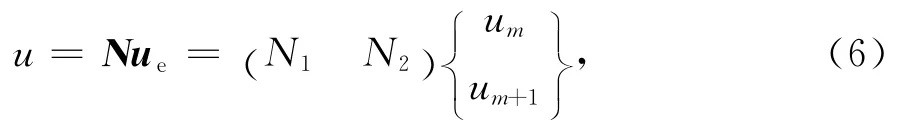
式中：um、um＋1分別代表節點m和節點m＋1處的超靜孔壓值；N1和N2為形函數，如式（7）所示。

式中：zm、zm＋1分別代表節點m和節點m＋1處的坐標值。

將式（2）和式（6）代入式（1），并利用Galerkin加權殘值方法，可得矩陣方程式（8）。

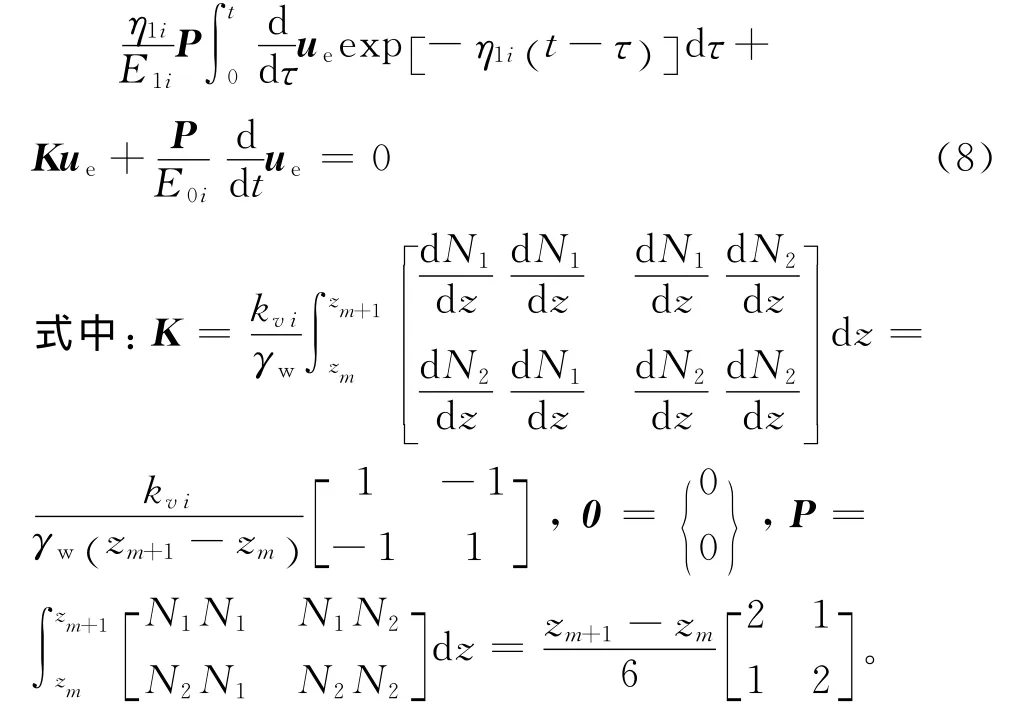
將時間分段，在時間段tj到tj＋1上孔壓均為變量，對時間變量進行線性插值，式（8）可整理為式（9）。

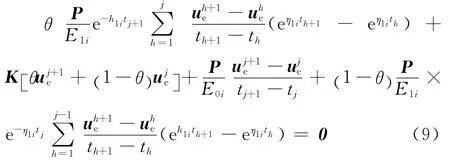
令θ＝1／2，即采用 Crank－Nicolson方法［15］，式（9）可整理為矩陣式（10）。

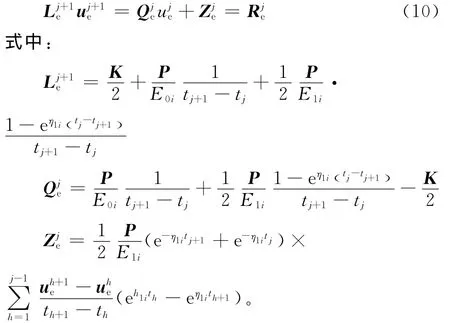
式（10）為每個單元的矩陣方程，采用常規的有限元總矩陣組裝方法［15］，形成總的矩陣方程如式（11）所示，從而進一步求解。

在形成總體矩陣后，由于第1個節點為排水節點，超靜孔壓為0。為方便程序編制，不改變總矩陣的行數和列數，令總矩陣第1行、第1列數加上很大的數，如1015，而方程的右端第一行設置為0。最后1個節點，其外部流量為0，不需做任何特殊處理，在有限元單元矩陣推導過程中已默認為無流量邊界。為了便于工程應用，采用Fortran語言將上述有限元求解方法編制成應用程序。

2.2 解答有效性驗證

若本文研究的層狀黏彈性地基僅有一層，即可簡化為單層黏彈性地基一維固結問題。若令Merchant流變模型ηi＝0，即為層狀線彈性地基一維固結問題。單層黏彈性地基和雙層線彈性地基是本文研究問題的2種特殊情況，其解析解答已分別被趙維炳［9］和Xie等［12］推導獲得。為了驗證本文求解方法和程序編制的正確性，采用本文程序分別對單層黏彈性地基的固結問題和雙層線彈性地基固結進行求解，并與已有精確解析解進行對比分析。

單層黏彈性土層厚度為10m，滲透系數kv＝2×10－9m／s，Merchant流變模型E0＝2MPa，E1＝5MPa，η1＝2×10－8s－1。將土層 劃分為 20 個0.5m等長單元，共計21個節點，時間間隔取為1d。圖2為100、500、2 000d時，本文有限元方法與解析解在不同深度處土體固結度比較情況。

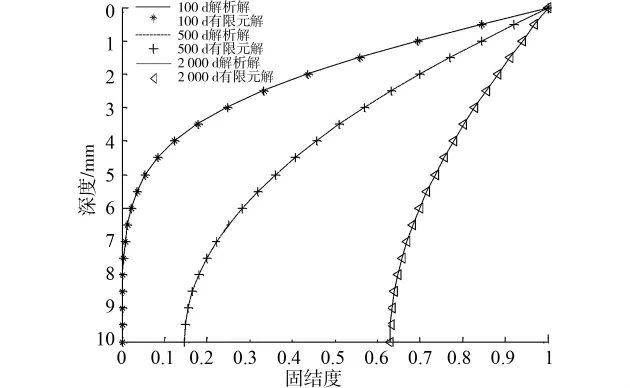
圖2 單層黏彈性地基有限元解與解析解比較

雙層線彈性土層厚度為10m，第1層土層厚度為3m，滲透系數kv＝1×10－8m／s，壓縮模量Es＝5MPa，第2層土層厚度為7m，滲透系數kv＝2×10－9m／s，壓縮模量Es＝2MPa。將土層劃分為20個0.5m等長單元，共計21個節點，時間間隔取為1d。圖3為100d，500d以及1 000d時，本文有限元方法與解析解在不同深度處土體固結度比較情況。

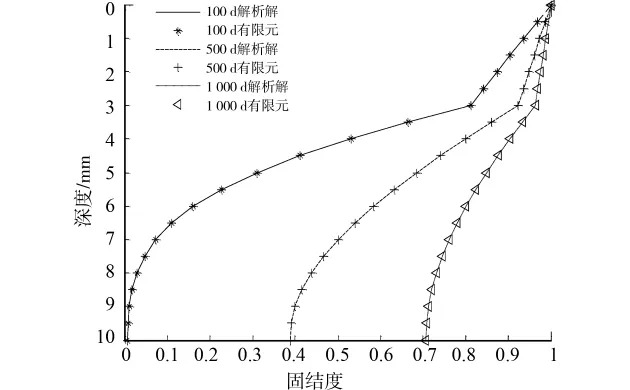
圖3 雙層線彈性地基有限元解與解析解比較

從以上2個算例的比較情況，可以看出，本文解答與解析解吻合較好，驗證了本文求解方法的有效性和程序編制的正確性。

3 層狀黏彈性地基固結特性分析

利用本文有限元求解方法，對1個3層黏彈性地基的一維固結問題進行研究，以揭示其固結規律。算例地基土層情況如表1所示：

表1 地基土層參數

圖4為考慮黏滯性和不考慮黏滯性時3層地基孔壓消散情況。從圖中可以看出，不管是黏彈性土體，還是線彈性土體，在土層的分界面處，孔壓消散會出現轉折點。在時間為100d時，土體的黏滯性對孔壓消散的影響并不明顯；500d時，第3層土層底部固結度相差10.47%；1 000d時，第3層土層底部固結度相差14.38%。說明，隨著時間的增加，孔壓消散差別越來越明顯，粘滯性土體的孔壓消散滯后于線彈性土體。從圖中還可以看出，在同一時刻，土體埋深越大，即離排水面距離越遠，黏彈性土體固結度越滯后于線彈性土體固結度。

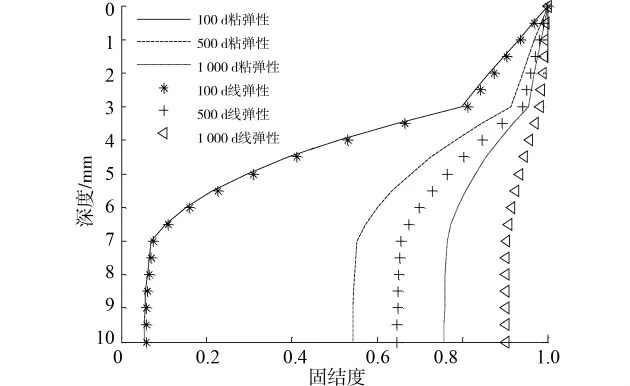
圖4 考慮黏滯性與不考慮黏滯性地基孔壓消散比較

圖5 為土層2和土層3中心點處土體孔壓消散隨時間變化情況。從圖中可以看出，第2層土體黏滯性土體對孔壓消散的影響，約在2d左右；而第3層粘彈性對孔壓消散的影響約在50d左右。說明隨著土層離排水面距離越大，黏滯性對孔壓消散的影響也越滯后。不管是第2層土體，還是第3層土體，隨著時間的增加，黏滯性土體孔壓消散越來越落后于線彈性土體，到某一時刻后兩者差距達到最大值，再隨著時間的延長，差距又會越來越小。在線彈性土體固結度達到80%～90%時，黏彈性土體與線彈性土體固結固結度差異較大。

圖6為第2層土體黏滯性參數η1從1.0×10－7變化到0，該土層土體中心點處孔壓消散情況，從圖中可以看出，當η1＝1.0×10－9時，與粘彈性土體與線彈性土體固結度差異較小，最大差異值為3%。η1越大，粘彈性土體與線彈性土體固結度差異越大，且對土體的固結度影響也越提前。

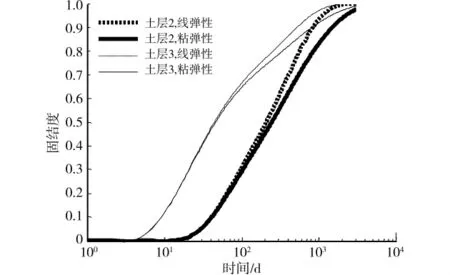
圖5 土體孔壓消散隨時間變化情況

圖6 流變參數η1對孔壓消散的影響

4 結 語

1）基于 Merchant流變模型，利用Galerkin加權殘值方法，推導了層狀黏彈性地基一維固結有限元矩陣方程，并給出了求解過程。采用Fortran語言將本文有限元求解方法編制成應用程序。通過單層黏彈性地基和雙層線彈性地基一維固結問題本文有限元解答與解析解答的比較，驗證了本文求解方法和程序的有效性。

2）對3層地基一維固結研究表明，在土層分界面處孔壓消散出現轉折點。黏滯性土體孔壓消散要滯后于線彈性土體，且隨著時間的延長，兩者差異會越來越大。同一時刻，隨著土體離透水面距離的增大，黏滯性影響會越大。

3）土體的粘彈性對孔壓消散的影響時間與其離排水面距離有關，土層離排水面距離越大，黏滯性對孔壓消散的影響時間也越滯后。黏滯性土體與線彈性固結度差異呈現兩頭小中間大的特點。工程中常要求地基固結度達到80%～90%，而這一時間段內考慮考慮土體的粘彈性和不考慮粘彈性固結度差異較大。因此，在實際工程中應考慮土體粘彈性對孔壓消散的影響。

4）土體粘彈性參數η1越大，則孔壓消散越慢，與線彈性土體固結度差異越大。在實際工程若η1＜1.0×10－9s－1時，粘彈性土體與線彈性土體固結度差異在3%以內，可以不考慮粘彈性對土體固結度的影響。

［1］Hsu T W，Lu S C.Behavior of one－dimensional consolidation under time－dependent loading［J］.Journal of Engineering Mechanics，2006，132（4）：457－462.

［2］Liu J C，Zhao W B，Zai J M.Research on seepage force influence on one－dimensional consolidation ［J］.Geotechnical Special Publication，2006，148：203－209.

［3］Qin A F，Chen G J，Tan Y W，et al.Analytical solution to one－dimensional consolidation in unsaturated soils［J］.Applied Mathematics and Mechanics，2008，29（10）：1329－1340.

［4］Morris P H.Analytical solutions of linear finite－and small－strain one－dimensional consolidation［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2005，29（2）：127－140.

［5］Yang L A，Tan T S.One－dimensional consolidation of lumpy clay with non－linear properties［J］.Geotechnique，2005，55（3）：227－235.

［6］鄂建，陳剛，孫愛榮.考慮低速非Darcy滲流的飽和黏性土一維固結分析［J］.巖土工程學報，2009，31（7）：1115－1119.E Jian，CHEN Gang，SUN Airong.One－dimensional consolidation of saturated cohesive soil considering［J］.Chinese Journal of Geotechnical Engineering，2009，31（7）：1115－1119.

［7］Xie K H，Xie X Y，Jiang W.A study on one－dimensional nonlinear consolidation of double－layered soil ［J］.Computers and Geotechnics，2002，29（2）：151－168.

［8］Lee P K K，Xie K H，Cheung Y K.Study on onedimensional consolidation of layered systems［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1992，16（11）：815－831.

［9］趙維炳.廣義Voigt模型模擬的飽水土體一維固結理論及其應用［J］.巖土工程學報，1989，11（5）：78－85.ZHAO Weibin.Theory of one－dimensional consolidation of saturated clays with generalized Voigt model and its applications［J］.Chinese Journal of Geotechnical Engineering，1989，11（5）：78－85.

［10］Hawlader B C，Muhunthan B，Imai G.Viscosity effects on one－dimensional consolidation of clay［J］.International Journal of Geomechanics，2003，3（1／2）：99－110.

［11］Li J Z，Peng F L，Xu L S.One－dimensional viscous behavior of clay and its constitutive modeling［J］.International Journal of Geomechanics，2009，9（2）：43－51.

［12］Xie K H，Xie X Y，Li X B.Analytical theory for onedimensional consolidation of clayey soils exhibiting rheological characteristics under time－dependent loading［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2008，32（14）：1833－1855.

［13］Cai Y Q，Xu C J，Yuan H M.One－dimensional consolidation of layered and viscoelastic solids under arbitrary loading ［J］.Applied Mathematics and Mechanics，2001，22（3）：307－313.

［14］劉加才，趙維炳，宰金珉，等.雙層黏彈性地基一維固結分析［J］.巖土力學，2007，28（4）：743－746，752.LIU Jiacai，ZHAO Weibing，ZAI Jinmin，et al.Analysis of one－dimensional consolidation of double－layered viscoelastic ground［J］.Rock and Soil Mechanics，2007，28（4）：743－746，752.

［15］Thomas J W.Numerical partial differential equations：finite difference methods［M］.Beijing：Beijing World Publishing Corporation，1997.

［16］Smith J M，Griffiths D V.Programming the finite element method［M］.4th ed.New York：John Wiley Sons Ltd.，2004.