PID控制器在磁懸浮球系統實驗中的應用

（海軍航空工程學院青島分院，山東 青島 266041）

PID控制器問世至今已有近70年歷史，其以結構簡單、穩定性好、工作可靠、調整方便而成為工業控制的主要技術之一。本文設計了一個PID控制器對實驗室已有的磁懸浮系統通過PID控制器參數的調整進行優化。然后利用Matlab軟件對控制系統進行了仿真并通過仿真圖形進行性能分析，實現了對磁懸浮球系統的穩定控制。實驗證實，該PID控制器的設計是正確可行的。

1 PID控制器系統的模型建立

實驗室建立的磁懸浮球系統如圖1。

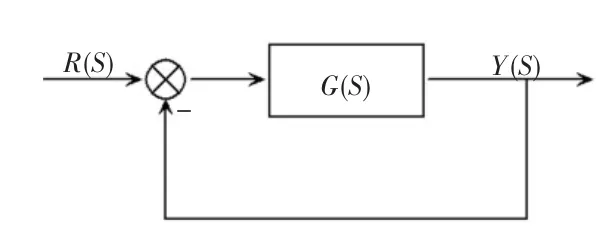
圖1 磁懸浮球結構圖

已知的磁懸浮球系統的傳遞函數為

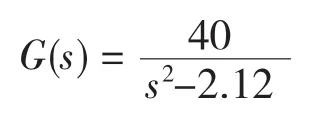
此時利用Matlab里的rlocus命令畫出該開環系統的根軌跡圖，如圖2。

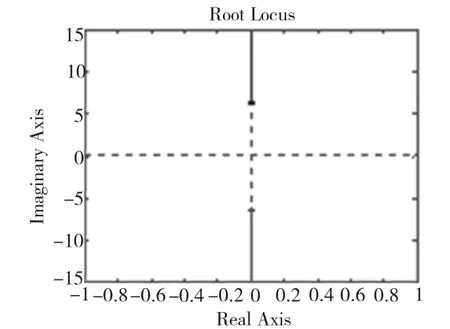
圖2 磁懸浮球系統根軌跡圖

對圖2進行分析可以看出，系統根軌跡分布在虛軸上，系統處于臨界穩定狀態，從現實意義上也是一種不穩定狀態，所以該控制器需要進一步的優化改進。

加入PID控制器后系統的方框圖形式如圖3。

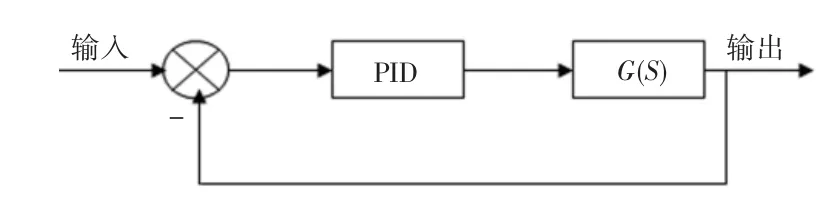
圖3 加入PID校正后磁懸浮球系統方框圖

設PID控制器的傳遞函數為

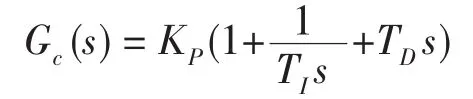
式中，

KP為比例系數；

TI為積分時間常數；

TD為微分時間常數。

此時，系統的閉環傳遞函數

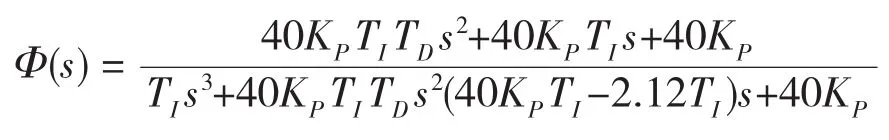
其特征方程為

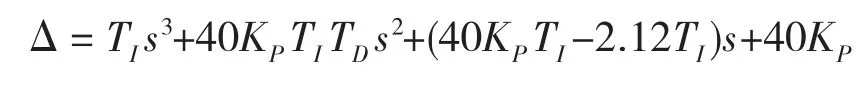
2 PID控制器KP、TI、TD這3個參數的選取

比例系數、積分時間常數、微分時間常數這3個參數的調整，主要根據它們對系統性能的影響來進行[1]。

比例系數KP對控制系統的影響：若 KP過大，則系統趨向于不穩定狀態；若過小，又會使系統的響應時間延長，影響系統快速性。

積分時間TI對控制系統的影響：積分時間常數通常會影響系統的穩定性。TI太小，系統會不穩定；太大對系統性能的影響減小。當TI取值合適時，系統過渡特性將會比較理想。

微分時間常數TD對控制系統性能的影響：TD偏大，會導致超調量增大，加大調節時間；偏小，調節時間也較長，只有TD取值合適時，才能有比較滿意的過渡過程。

至于微分時間常數TD和比例系數KP根據最佳阻尼比已經計算出結果

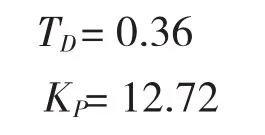
所以只需要確定積分時間常數TI的數值，就可以確定PID控制器的傳遞函數。

對于積分時間常數TI的確定，我們采用臨界靈敏度法[2]，具體做法如下：

當已知系統的臨界比例增益KC和振蕩周期TC時，也可以用經驗整定公式來確定PID控制器的參數

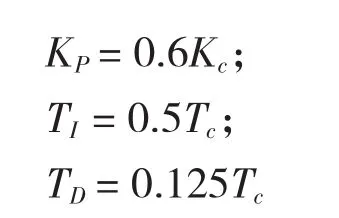
其中，特征參數Kc和Tc一般由系統整定實驗確定，或者用頻率特性分析算法，根據受控過程G(s)直接計算結果，即由增益裕度確定Kc，由截止頻率ωc確定 TC，即

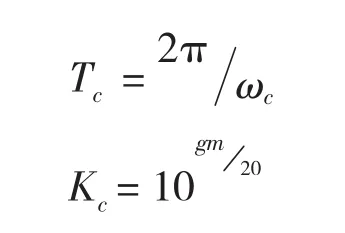
根據開環系統傳遞函數，即受控過程G(s)的截止頻率ωc=6.15 rad/s，由此可以計算得到振蕩周期TC=1.02，由于 TI=0.5 TC，得到 TI=0.51。

至此KP、TI、TD都已經計算得到了，數值分別為

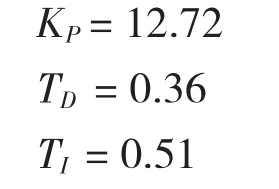
則PID控制器的傳遞函數為

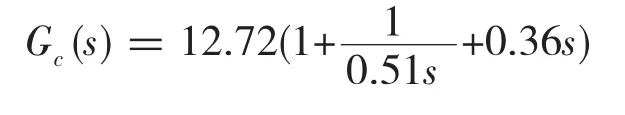
3 加入PID控制器后磁懸浮小球控制系統性能分析

加入PID控制器后，磁懸浮小球控制系統的閉環傳遞函數為

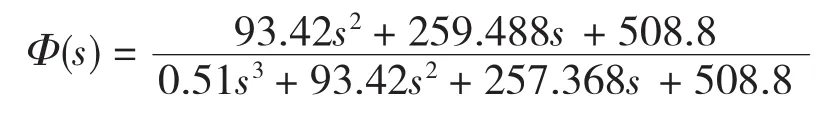
加入PID控制器后，系統對干擾信號的反應情況，利用Simulink仿真軟件進行仿真，在干擾信號為階躍信號作用下，系統的響應情況如圖4所示。

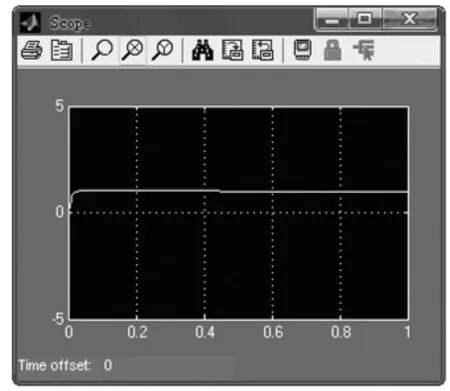
圖4 PID控制器階躍信號系統響應圖

從示波器的輸出波形可以明顯看出，加入PID控制器后，小球的抗干擾能力明顯提高，能夠維持穩定懸浮，說明采用PID控制器進行校正，能夠滿足控制要求。

另外，觀察此時的伯德圖和奈奎斯特圖也能夠證明這一點。

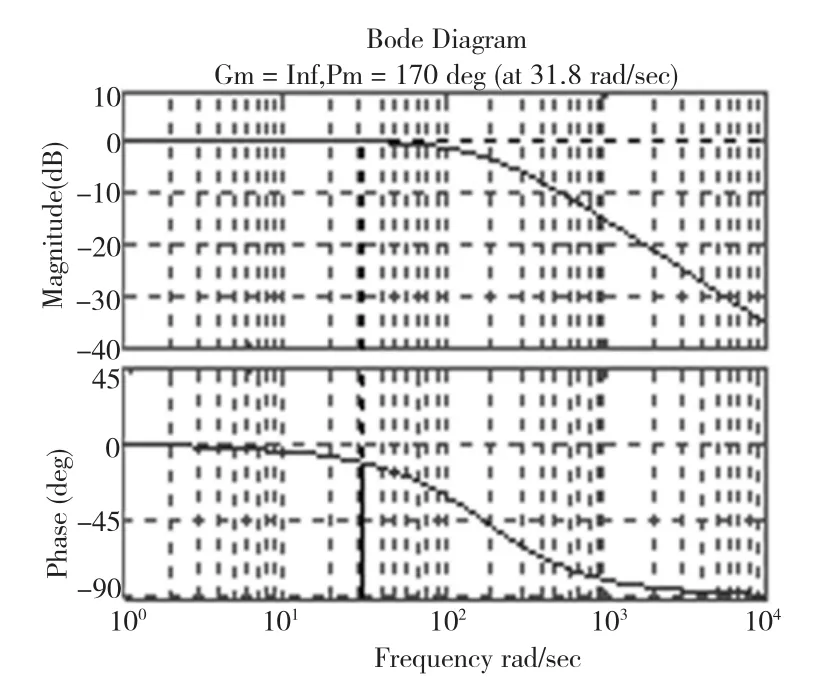
圖5 校正后系統的伯德圖

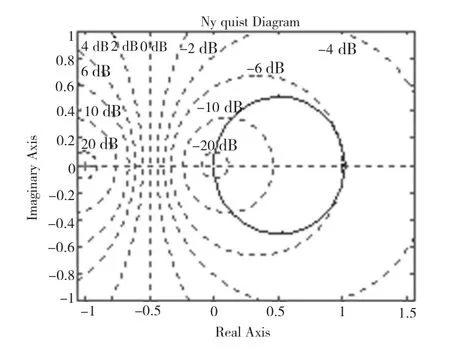
圖6 校正后系統的奈氏曲線圖

由于系統沒有右半平面的開環極點，從圖6可以看出，開環幅相曲線不包圍（–1，j0）點，系統穩定。另外，由圖5可以得系統的相角裕度γ=170°，由奈氏判據可知，系統閉環穩定。

4 結束語

綜上分析可以看出采用PID控制器可以使得系統的型別提高一級外，還能提供兩個負實部零點，不僅有效抑制了高頻干擾信號，提高了系統穩態性能，還提高了系統的反應速度，在系統動態性能方面，具有更大的優越性。

[1]任彥碩.自動控制原理[M].北京：機械工業出版社，2004.

[2]陶永華.新型PID控制及其應用[M].北京：機械工業出版社，1998.