一種基于Matlab的模糊控制系統優化設計方法
劉 亮
(海軍裝備部,西安 710025)
模糊控制是基于規則的一種智能控制方式,它不依賴于被控對象的精確數學模型,特別適用于多輸入-多輸出的強耦合性、參數的時變性和嚴重的非線性與不確定性的復雜系統。且控制方法簡單,實際效果好。其實質是對人觀察、思考、判斷、決策的思維過程的一種模擬,模糊控制器的設計在很大程度上依賴于設計者的經驗,帶有主觀性[1]。因此,需要對控制器進行優化才能取得較為滿意的設計效果。
Matlab軟件是由美國Math Works公司推出的專門用于科學、工程計算和系統仿真的高級語言,它集數值分析、矩陣運算、信號處理和圖形顯示于一體,并且提供了大量應用于不同學科的工具箱,編程效率高,使用簡單方便。特別是Simulink工具箱和FUZZY工具箱使得控制系統的設計與仿真變得相當容易和直觀。本文在Matlab6.5的基礎上介紹了如何構造模糊控制系統的結構框圖和進行仿真研究,對某火炮調速系統的控制器進行設計仿真,提供了一種模糊控制系統的高效仿真方法。
1 基于Matlab的模糊控制仿真系統的設計
模糊控制系統設計的關鍵是模糊控制器的設計,其參數主要有:各輸入、輸出變量模糊子集的隸屬度函數,模糊控制規則,輸入輸出變量的比例變量因子等。偏差和偏差變化作為模糊控制器的兩個輸入量,先對它們進行模糊量化處理,得到模糊變量E和EC,按模糊控制規則進行模糊決策,得到模糊控制量U,再經過解模糊和比例變換得到實際控制量輸出。
1.1 模糊控制器的設計
在Matlab中,可以借助于模糊系統工具箱的圖形用戶界面(GUI)工具編輯隸屬度函數和控制規則,這里以某火炮調速系統的開環傳遞函數作為設計控制器以及仿真的基礎。
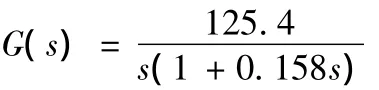
設控制系統的輸入為單位階躍信號r,輸出為y,誤差為e,誤差導數為de;模糊控制器的輸入為e、de,其輸出為u,所對應的模糊語言變量為E、DE和U,其論域范圍均取[-6,+6],模糊子集均為{NB,NM,NS,ZO,PS,PM,PB}。控制規則是對專家的理論知識和經驗的總結,此處共有49條規則,如表1所示。在RulesEditor窗口中輸入這49條控制規則[2]。例如:If E is NB and DE is NB then U is PB。
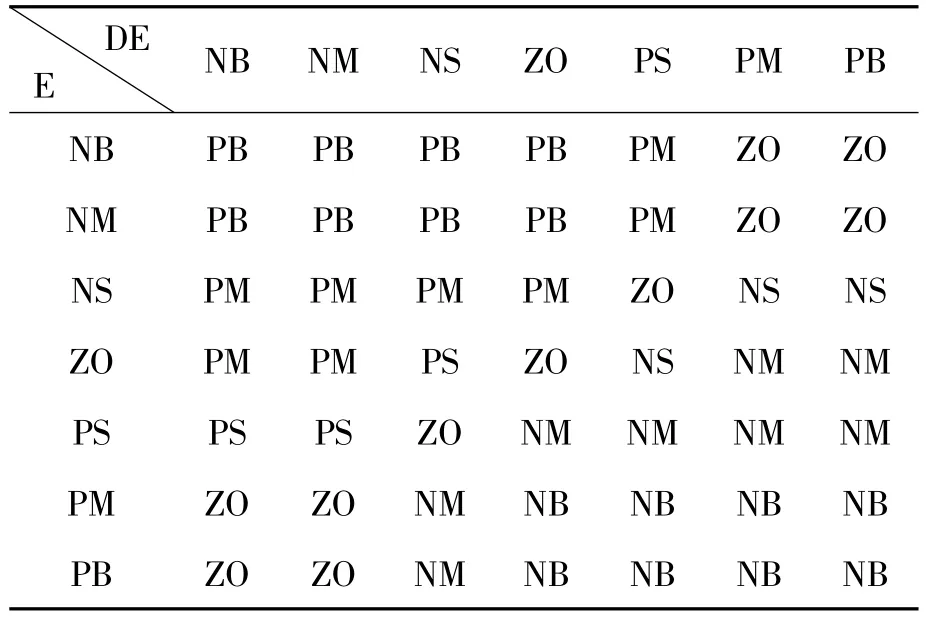
表1 模糊控制規則
在Matlab中鍵入FUZZY,進入模糊編輯窗口FISEDITOR。建立E、DE、U的隸屬度函數,有三角形、高斯形、梯形等11種可供選擇,在此選用常用的三角形隸屬度函數,如圖1所示。
模糊決策采用與方法為min,或方法為max,推理方法為min,合成方法為max,解模糊化方法為重心法(centroid)。建立的FIS文件取名為aa.fis.如此設計的模糊控制器的輸入與輸出的關系曲線如圖2所示,顯然模糊控制是一種非線性控制。
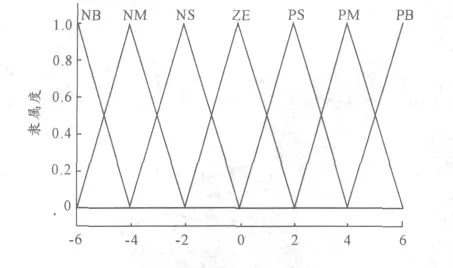
圖1 E/DE/U的隸屬度函數
1.2 Simulink仿真模型的建立
Simulink工具箱是Matlab軟件的擴展,主要用于動態系統的仿真.Simulink模塊庫中提供了建立系統模型所需的大部分模塊,進入Matlab環境后,鍵入Simulink命令就可打開該模塊庫,用戶可以根據自己的系統選擇所需的模塊,用鼠標將其拖至自己的系統模型中,其中在模糊控制工具箱中有一個模糊控制器模塊(Fuzzy Logic Controller),將這些模塊連接起來構成系統結構圖.雙擊各個模塊輸入相應的參數,其中模糊控制器的結構變量取aa,連接好各模塊,就構成了圖3所示的系統的Simulink描述.系統的模型建好后,用戶可以根據系統的不同需要,設置或更改模塊的參數,然后打開仿真菜單設置仿真參數,啟動仿真過程[3].這里仿真時間設置為 10 s,采樣周期設置為 0.01 s。
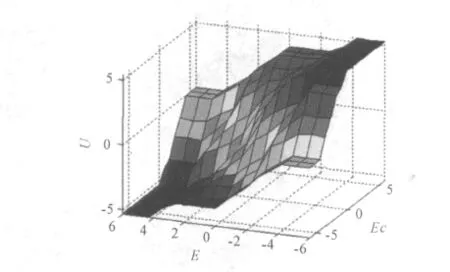
圖2 模糊控制器的輸入輸出曲線
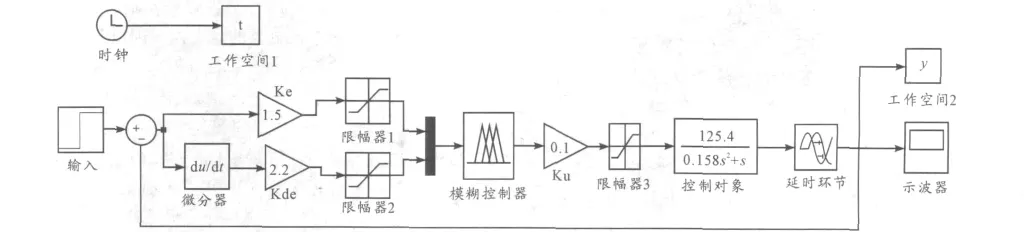
圖3 模糊控制系統仿真框
2 模糊控制系統的優化
上述模糊控制器是在特定的條件下設計的,其參數ke、kde、ku及其控制規則是根據經驗確定的,一般情況下這些參數不會是最佳值。量化因子ke、kde的大小對控制系統的動態性能影響很大。ke選得大時,系統的超調也較大,過渡過程較長,但可以使上升時間變短;kde選擇較大時,系統超調較小,但系統的響應速度變慢,ke、kde兩者之間也相互影響。ku選擇過小會使系統動態過程變長,過大又會導致系統震蕩加劇[4-5]。
S函數是擴展Simulink功能的有力工具,給用戶提供編寫復雜函數、創建系統未提供的模塊功能。在此編寫M文件的S函數,對ke、kde、ku進行自調整,優化控制效果。另外引入一個Ⅰ型積分環節用來消除固有的靜態誤差,編寫的S函數如下:
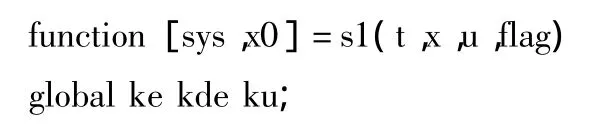

將編寫的S函數存盤為s1.m文件,按圖4(a)創建子系統,并對其封裝,如圖(b)。重新構建的模糊控制系統結構框圖如圖5所示。
對上述2種模糊控制系統框圖運行仿真后得到圖6所示結果,很顯然,參數調整時的仿真結果優于參數固定時的結果。
3 結束語
本文基于Matlab軟件,采用模糊控制的圖形用戶界面(GUI)創建模糊控制器,應用Simulink構造模糊控制的系統結構框圖進行仿真,減少了編程工作量,而且形象直觀、方便快捷。另外編寫了S函數,根據誤差大小實現參數自調整,通過引入一個Ⅰ型積分環節用來消除模糊控制固有的靜態誤差,同時,改善了模糊控制的控制效果。
[1] 樓順天,胡昌華,張偉.基于Matlab的系統分析與設計——模糊系統[M].西安:西安電子科技大學出版社,2001.
[2] 張葛祥,李娜.Matlab仿真技術與應用[M].北京:清華大學出版社,2003.
[3] 李祖欣.Matlab在模糊控制系統設計和仿真的應用[J].系統仿真學報,2003(1):132-134.
[4] 宋哲英,宋雪玲,劉朝英.應用Matlab設計模糊控制系統[J].計算機應用研究,2001(2):69 -71.
[5] 侯北平,盧佩,陳鋒軍.Matlab下模糊控制器的設計與應用[J].測控技術,2002(10):40-42.
(責任編輯周江川)

