響應曲面法在現金流預測中的應用
劉洪久,胡彥蓉,Robert Rieg,馬衛民
(1.常熟理工學院,江蘇 常熟 215500;2.Hochshule Aalen,Aalen,德國 73430;3.同濟大學,上海 200092)
0 引言
現金流是企業生命的血液,是衡量企業經營績效的重要指標,是企業價值的具體體現。沒有現金流,企業生存和發展就失去了基礎。是現金流將公司的日常經營以及投融資活動緊密地聯結在一起,其大小不僅決定著公司的支付能力,更是企業增長和創造價值的財務源泉。因此,不管是決策者、投資者和銀行,如果能對企業未來的現金流量作出較為準確的預測,就可以對企業未來經營業績作出完整客觀的綜合評價[1],從而進行科學合理的決策。本文采用的響應曲面法是一種回歸設計的方法。該方法通過尋找未來現金流量和歷史現金流量間的定量規律(而不是判斷因子的顯著性,找出各因子水平的最佳組合)預測未來現金流量。
1 樣本數據來源和滑動窗參數的確定
1.1 樣本數據來源
如果樣本數據不同,很難判斷方法的優劣。為了測試研究方法預測的準確性,需要采用同一數據。這里采用一汽轎車(股票代碼000800)從2002年12月31日到2011年3月l5日34個現金流數據(每季度)。現金流量用CFt表示(t=0,1,…,n),n表示時間序列的長度。
為了便于仿真,所有的數據都被歸一化(0,1),如公式(1):
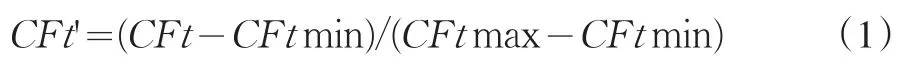
式中CFtmax和CFtmin分別表示現金流時間序列的最大值和最小值。
1.2 滑動窗參數確定
滑動窗口包括發送器和接收器,發送器和接收器的尺寸大小分別用wt和wr表示[2]。為了研究在什么樣的尺寸下,模型具有良好的預測效果,需要確定合適的發送器的尺寸[3],為此我們改變wt從1到8(wt=1,2,… ,8))。接收器的大小為1(wr=1)(見圖1),因為模型的輸出僅有一個結果。這樣,當我們同時滑動發送器和接收器的時候,就會得到模型的輸入矩陣P(i,j)(i=1,2,…,wt;j=1,2,…,n-wt)和輸出矩陣T(j)(j=1,2,…,n-wt)(見公式2、3)。
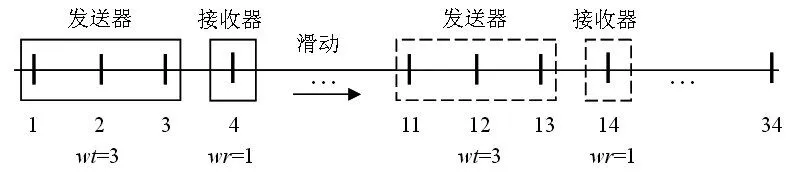
圖1 滑動窗口的發送器和接收器(wt=3)

P(i,j)和T(j)各自被劃分為培訓數據和測試數據兩組,每組培訓和測試數據都包括P(i,j)和T(j)。例如,數據組1由P(1,j)和T(1)(j=1,…,wt)。測試數據組中包含三對輸入和輸出向量用于檢驗模型的性能,培訓數據組用來訓練模型。
如果我們假定t時間的現金流量由t-1,t-2,…,t-wt時刻的現金流量決定,那么我們會構建函數f:Rwt→R的映射,從而得到t時刻的CF估計值:
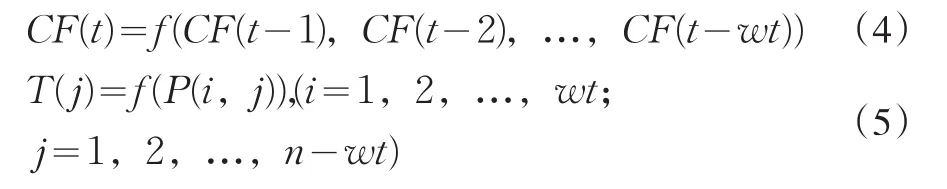
2 響應曲面模型的建模和仿真
在統計學中,響應曲面法(RSM)主要用于構建多個解釋變量和一個或多個響應變量之間的關系,該方法是1951年由Box和Wilson提出[4]。RSM是一種優化生物過程的統計學試驗設計,采用該法以建立連續變量曲面模型,對影響生物過程的因子及其交互作用進行評價,確定最佳水平范圍[5]。如果設y代表輸出,xi(i=1,2,…,n)代表輸入,響應曲面方程可以表示為公式(6)。
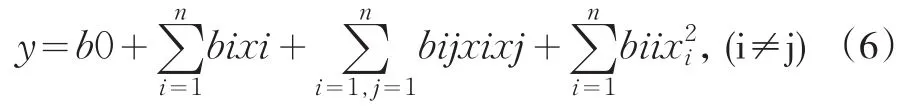
式中:
b0—常數項;
bi—一次項系數;
bij—交叉項系數;
bii—二次項系數。
模型在Matlab 2009b環境中訓練和測試,需要引用Matlab統計工具箱中的rstool函數計算b0,bi,bij,bii。對于函數rstool,有四個函數可以選擇:Linear,Pure Quadratic,Interactions和Full Quadratic。
Linear—方程包括常數和一次項系數;
PureQuadratic—方程包括常數項、一次項和二次項系數;
Interactions—方程包括常數項、一次項和交叉項系數;
Full Quadratic—方程包括常數項、一次項、交叉項和二次項系數[6]。
四個函數的訓練效果取決于它們的均方根誤差的大小。顯然,均方根誤差越小,模型的訓練效果越好。我們將訓練樣本數據輸入各模型可得每個模型的均方根誤差(見表1)。
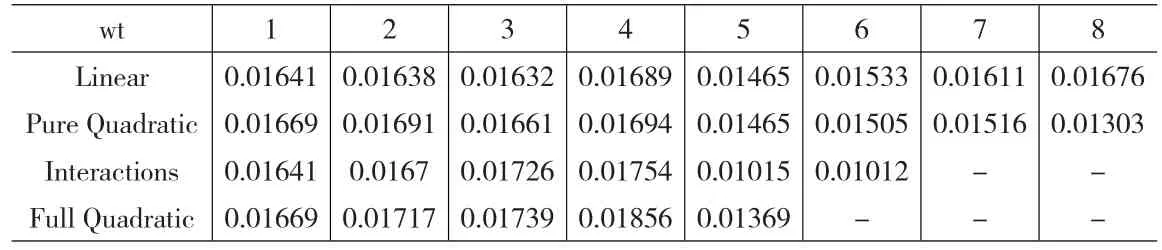
表1 不同函數的均方根誤差rmse
根據表1數據,當wt等于6時,Interactions函數的擬合效果最好,均方根誤差最小(rmse=0.01012)。圖2是Interactions函數的訓練結果圖。
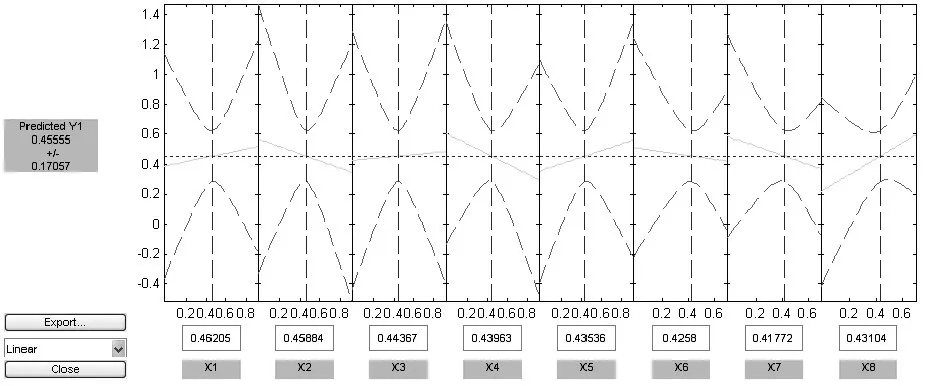
圖2 Interaction函數的訓練結果
將rstool函數的計算結果輸入到Matlab的workshop可得在不同的滑動窗發送器尺寸下(wt=1,2,…,8),Linear、Pure Quadratic、Interactions和Full Quadratic函數的各項系數b0、bi、bij和bii。將各項系數和測試數據帶入公式(6),可計算預測值的相對誤差。具體見表2。
觀察表2,我們會發現,滑動窗發送器的尺寸為wt=7,訓練函數為Linear時,預測的相對誤差最小(8.0113%)(見圖3)。對比模型的訓練和測試過程,即表1訓練的結論和表2測試的結論不一致,因為表1的結論為:wt等于6時,Interactions函數的擬合效果好。所以,在運用響應曲面模型時,不能單純的運用樣本訓練的結論簡單的去預測未來的現金流。要在對模型訓練的基礎上測試不同發送器尺寸和函數的條件下,才能得出合理的結論。
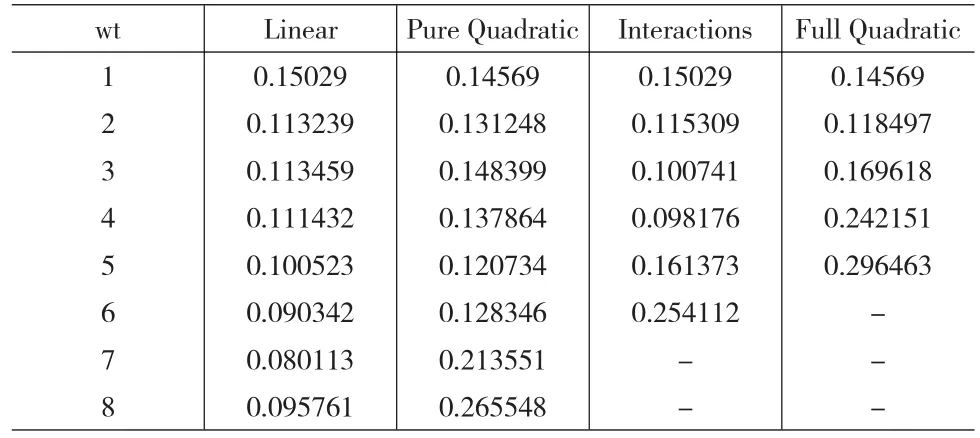
表2 預測值的相對誤差
3 結論
通過對響應曲面法的建模和仿真,可以發現,作為一種回歸設計方法,響應曲面模型與其它時間序列方法(指數平滑法、移動平均法、曲線趨勢預測法等)一樣,都具有良好的預測功能。響應曲面模型的訓練效果和預測性能與滑動窗口的發送器尺寸wt和具體的響應曲面模型函數有關。通過對一汽轎車公司現金流預測的實證研究表明,當滑動窗發送器尺寸wt等于6時,Interactions函數的擬合效果好;而當滑動窗發送器的尺寸wt等于7時,Linear函數的預測相對誤差最小。因此,應用響應曲面模型做預測時,既要考慮樣本訓練的結論,又要驗證樣本預測的效果,這樣才能合理的預測企業的現金流,從而為科學決策提供依據。
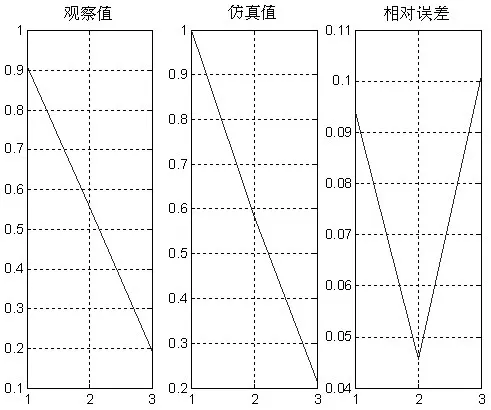
圖3 RSM法中wt=7時的預測效果
[1]韓立巖,婁靜.經營、投資和籌資現金流動態交互影響分析[J].中國管理科學,2010,(2).
[2]Khan M S,Coenen F,Reid D,et al.A Sliding Windows Based Dual Support Framework for Discovering Emerging Trends from Temporal Data[J].Knowledge-Based Systems,2010,23(4).
[3]Chu C J.Time Series Segmentation:A Sliding Window Approach[J].Information Sciences,1995,85(1~3).
[4]Box G E P,Wilson K B.On the Experimental Attainment of Optimum Conditions[J].Journal of Royal Statistical Society,1951,8(1).
[5]Crispim E G,Piai J F,Muniz A F R A.Addition of Methacryloil Groups to Poly(Vinyl Alcohol)in DMSO catalyzed by TEMED:Opti?mization through Response Surface Methodology[Z].2006.
[6]周紀薌,茆詩松.求響應曲面的極小極大估計的計算機方法[J].華東師范大學學報(自然科學版),1983,(3).

