廣州新塔不同激勵下動力特性監測
陳偉歡,呂中榮,陳樹輝,倪一清,廖渭揚
(1.中山大學 應用力學與工程系,廣州 510275;2.香港理工大學 土木及結構工程系,香港)
隨著我國經濟和建筑技術的發展,超高聳結構日益增多。如即將竣工并將在2010年廣州亞運會投入使用的廣州新電視塔,廣州西塔以及即正在興建的廣州東塔和上海中心等,都屬于超高聳結構。在動力特性方面,這類超高聳結構的第一階振動頻率很低,如廣州新電視塔的第一階振動頻率不到0.1 Hz,屬于高柔結構,對風荷載和長周期地震非常敏感,所以結構既要考慮抗震也要考慮抗風,近幾年全球地震頻繁,而廣州市又地處臺風帶,夏季臺風影響頻繁,因此對廣州新電視塔進行不同激勵下的動力特性監測,動態的了解結構在日常使用環境下以及在強臺風、地震等災害性荷載下的結構性態,不僅可以進行極端災害情況下的安全性預警,為業主進行災害的應急管理提供決策依據,并且可為抗震減振設計提供寶貴的基礎資料,為超高層建筑結構新技術的研究提供重要參考。本文作者已經對廣州新電視塔臺風期間的動力特性做了一些研究[1]。
廣州新電視塔高610 m,是廣州市新的地標性重點工程,如圖1所示。其結構超高、形體奇特、結構復雜,在超高層建筑發展史上具有里程碑的意義。因此,在建造過程中的施工監控與運營期間的健康監測都具有十分重要的意義,一個包括超過700個傳感器的長期結構健康監測系統已經廣州新電視塔上運行[2],而結構的動力特性測試正是監測內容的重要組成部分之一。

圖1 廣州新電視塔Fig.1 Canton Tower
以廣州新電視塔為背景,介紹了其結構健康監測系統中的振動測試子系統。利用該子系統測得的不同激勵下結構的加速度響應數據,首先,比較了在不同激勵下結構的加速度時程響應和功率譜密度。然后,利用加速度響應數據進行模態分析并比較了在不同激勵下結構的模態參數(包括頻率、振型和阻尼比)。最后,利用希爾伯特-黃變換獲得結構在不同激勵下的瞬時頻率和結構響應能量分布,并與小波變換的結果相比較。結果可為了解超高層建筑在不同激勵下的動力特性提供參考。
1 振動測試系統
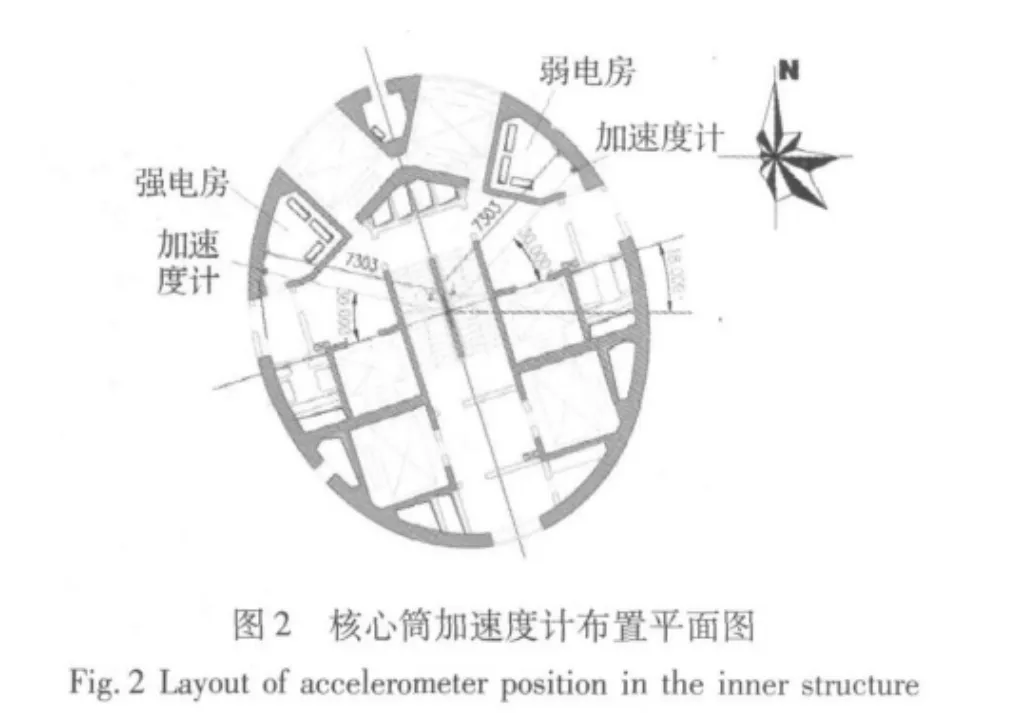
振動測試中加速度傳感器全部布置在核心筒內8個監測斷面上,其高程分別為 30.63 m、119.30 m、171.10 m、228.50 m、275.30 m、332.15 m、384.24 m 和446.80 m。除了截面 4(即 228.50 m)和截面 8(即446.80 m)布置4個加速度計外,其他每個截面上布置2個加速度計。每個截面的兩個測點分別位于核心筒的強電房與弱電房里,其平面圖如圖2所示。
強電房的所有加速度傳感器均布置為X方向(短軸方向),弱電房的所有傳感器均布置為Y方向(長軸方向),第四和第八個截面每個測點在X方向和Y方向各布置一個加速度計。
數據采集系統采用分布式同步測量系統(如圖3),在8個測量截面的弱電房里各安置一個采集子站,用于采集該截面的加速度響應數據。8個子站用網絡線連接起來。進行加速度信號采集時,采集系統通過發送一同步信號以達到各個采集子站同步采集的效果,最后將數據存儲在PC機上。關于該振動測試系統更多詳細資料可參考文獻[3]。
由于能夠自動連續的采集并存儲數據,該振動測試系統已經成功的監測到多次地震或臺風激勵下廣州新電視塔的結構動力特性。本文主要分析2009年12月19日臺灣花蓮地震,2009年9月15日臺風巨爵及一般風荷載激勵下結構的動力特性。

2 結構動力響應
廣州塔在不同激勵下的動力響應特性可簡化認為是多自由結構的受迫振動,結構的動力響應特性與激勵密切相關。不同激勵荷載的顯著頻段不同,從而激發結構不同頻段的模態頻率。由于風脈動的頻率非常低,所以結構在風荷載特別臺風激勵下一般表現出以最低幾個頻率的能量響應為主。地震激勵的顯著頻率較風荷載高,一般為0.1 Hz到10 Hz不等,所以結構在地震激勵下所表現出來的主要模態頻率較風荷載激勵下的要高。
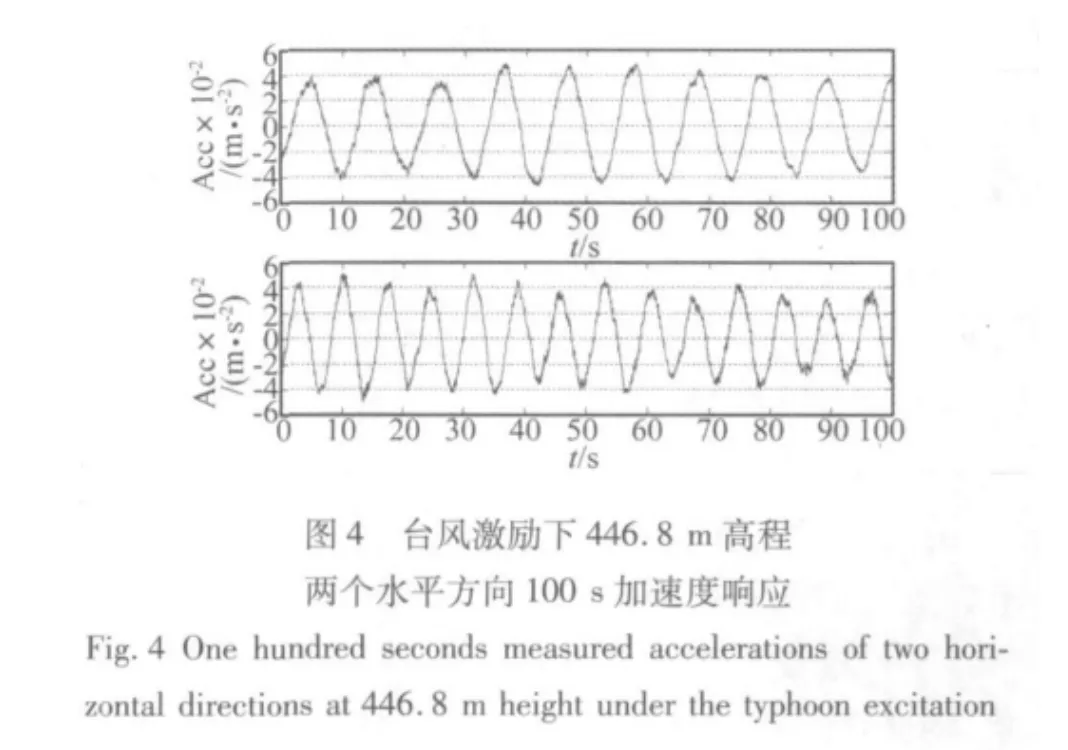
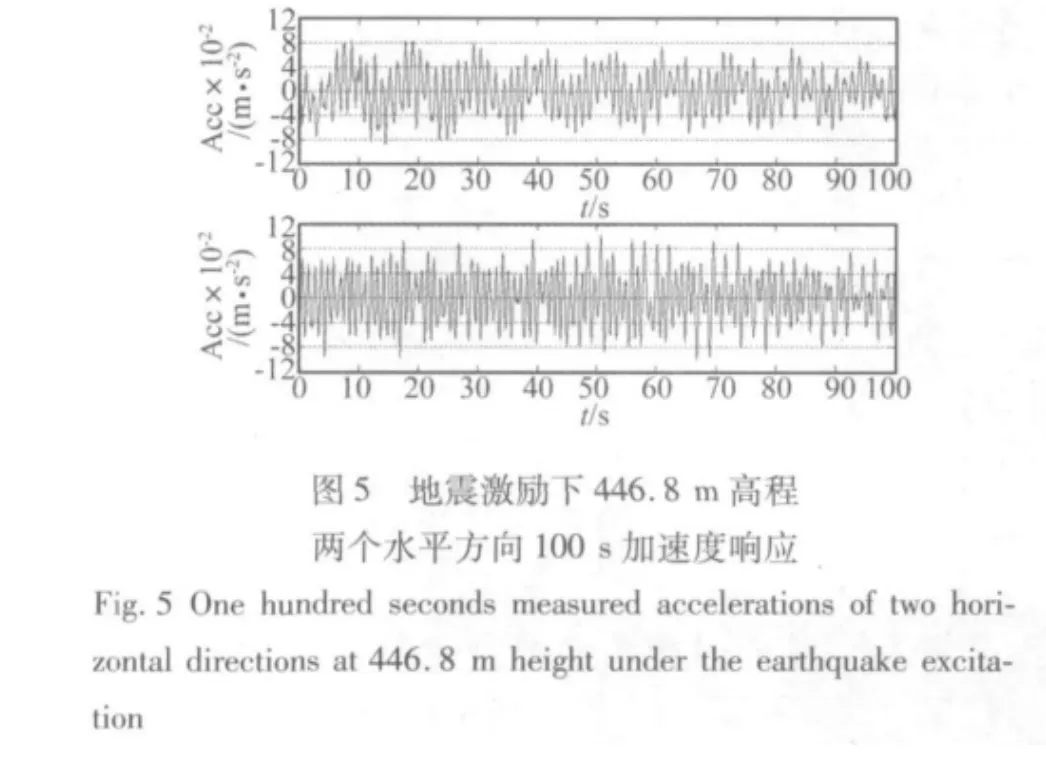
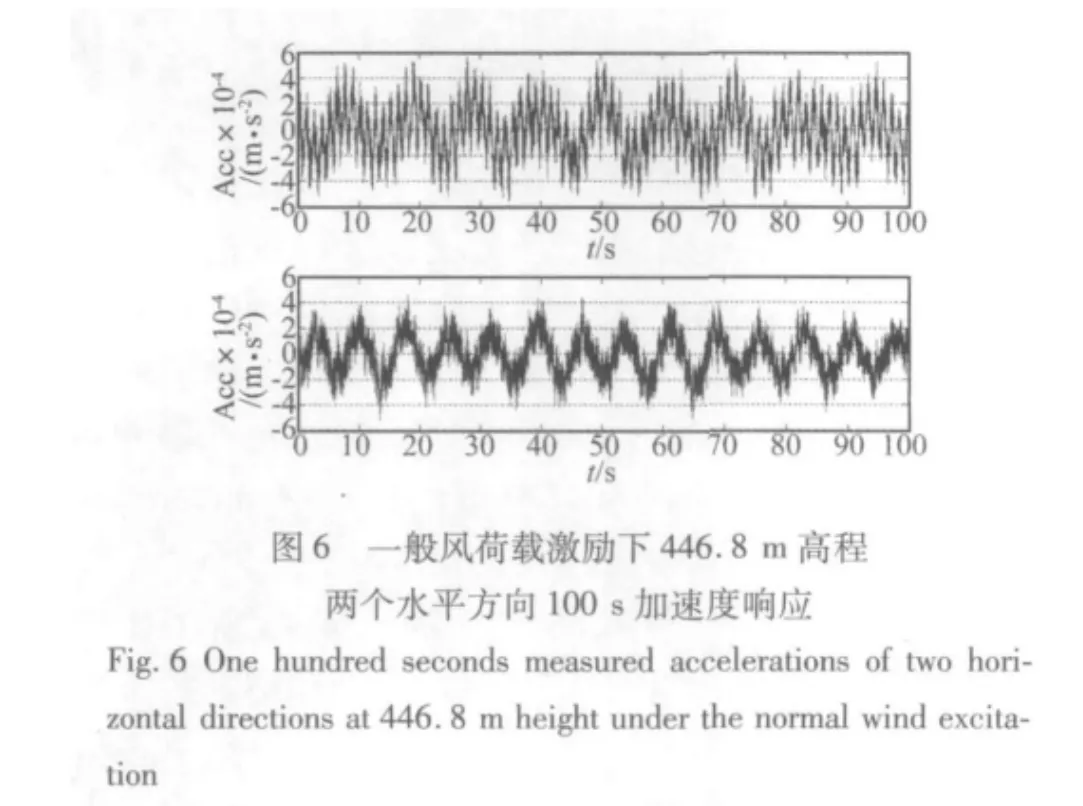
如圖4至6分別展示了臺風、地震和一般風荷載激勵下446.8 m高程兩個水平方向100 s的加速度響應。從這三個時程圖上可以看到不同激勵下結構的加速度響應有很大的不同。在臺風激勵下,結構的加速度響應大約為0.05 m/s2,前兩階的低頻響應清晰可見,兩個周期大約在0.1 Hz和0.14 Hz左右。在地震激勵下,結構的響應頻率要比在臺風激勵下的主要頻率高的多,從時域上較難看清主要頻率的精確大小,由于地震距離廣州新電視塔較遠,所以結構的響應并不是特別大,大約為0.01 m/s2。在一般風荷載激勵,結構的響應較小,也是以低頻為主,低頻響應中夾雜著高頻響應。
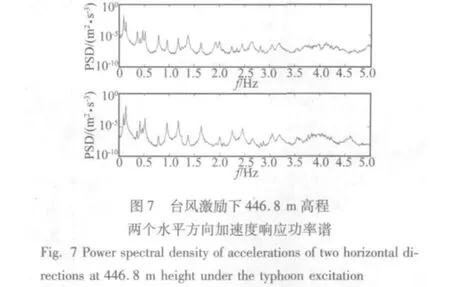
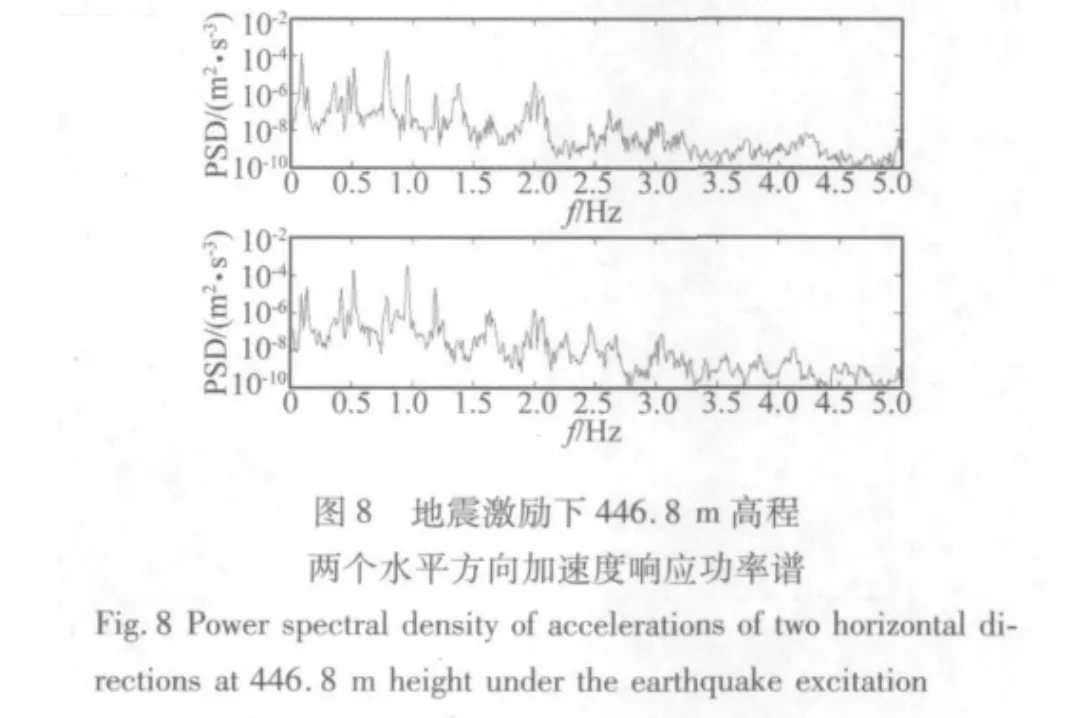
進一步分析數據,對加速度響應數據作平均功率譜密度估計,如圖7至圖9所示,結構在不同激勵下都呈現出密頻并且多模態耦合的形態,但是在不同激勵下結構最顯著的模態頻率不同。在臺風激勵下,結構的加速度風振響應以最低兩階模態頻率為主。在地震激勵下,結構的加速度地震響應以0.8 Hz和1 Hz左右兩個模態頻率為主。在一般風荷載激勵下,結構以較低幾個模態頻率為主。

3 模態分析
在過去的一段時間里,由于土木工程結構規模巨大無法采用人工激勵,僅基于輸出或者叫做基于環境振動的模態分析已經在結構健康監測得到廣泛的應用。目前,國內外研究者提出了多種僅基于輸出響應的模態參數識別方法。本文同時考慮算法的準確性和穩定可行性,最終采樣頻域分解法(Frequency domain decomposition)進行模態參數識別。
頻域分解法[4]是峰值拾取法的延伸,克服了峰值拾取法的缺點,主要思想是:對響應的功率譜進行奇異值分解,將功率譜分解為對應多階模態的一組單自由度系統功率譜。該方法識別精度高,有一定的抗干擾能力。已在一些大型土木結構的模態識別中成功應用[5-6]。
采用頻域分解法,利用不同激勵下結構的加速度響應,識別了不同激勵下結構的模態參數。前十階頻率和阻尼比識別結果見表1。另外,圖10還給出了前四階歸一化振型的比較。
從表1可以看出:① 不同激勵下結構的頻率略有不同,這可能與輸入的激勵有關,也可能與環境因素(如溫度、濕度等)有關。但可以確定的是,實際結構的固有頻率不是一成不變的,而是隨著溫度和激勵的變化而略有變化。環境因素可以影響結構的剛度從而影響頻率。并且實際結構存在非線性,非線性結構的振動頻率受諸多因素(其中包括激勵)影響,大型工程結構的隨機非線性理論和研究方法目前尚未完善。②阻尼比的識別結果相差較大,這與阻尼比的復雜機制有關。③ 在一般風荷載激勵下,結構第十階模態很難識別出來。
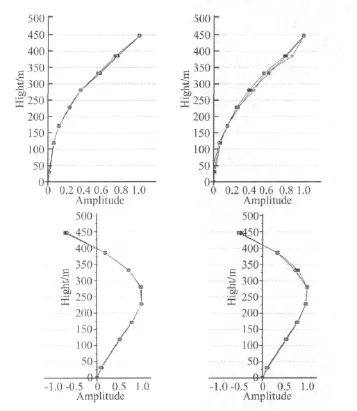
圖10 不同激勵下前四階振型比較Fig.10 Compare the first four modes shape under different excitation condition
4 時頻分析
時頻分析方法因能同時在時域和頻域內觀察信號的演變,提供信號的局部時頻特征,因而不僅能分析平穩信號且能分析非平穩信號。由于時頻聯合分析方法與傳統的時域和頻域分析方法相比具有不可比擬的優點,使其不僅在信號處理領域內得到了迅速的發展,而且在其他領域如土木工程領域也得到了廣泛的應用[7]。土木工程中的地震工程、防災減災、結構抗震分析及健康監測等領域都會遇到非平穩信號的處理問題,因此,將信號處理中新的發展成果應用于土木工程中,極大地促進了該領域的發展。而在眾多的時頻分析方法中,小波變換和希爾伯特-黃變換(HHT)兩種方法受到很大關注。
小波變換通過對母小波進行尺度伸縮和平移得到的子小波進行分解,在時間尺度域內分析信號的一種時頻分析方法。小波變換克服了短時傅里葉變換固定時窗、恒定分辨率的限制,具有多分辨分析的性質。然而從本質上講,小波變換是一種窗口可調的傅里葉變換[8],擺脫不了傅里葉變換的局限,同樣會存在能量泄露,受到不確定性原理的限制。本文分析采用目前最為廣泛應用的Morlet小波。
Hilbert-Huang變換包括經驗模式分解(EMD)和Hilbert變換兩部分。在時域內將信號自適應地分解為多個在任意時刻只有單一振蕩的內在模態函數(IMF)和一個剩余分量,并在分解過程中保持信號本身的特性,分解后對每個IMF進行Hilbert變換得到瞬時頻率和瞬時幅值。經驗模態分解基于瞬時頻率的觀點,打破了不確定性原理的限制,對信號的局部信息進行分析,因此得到的時頻譜具有很高的時頻分辨率[9]。作為一種新的方法,雖然已經成功應用于很多研究領域,但是仍然存在很多問題,如邊界效應,模態分量之間不完全正交等[9]。對于結構的加速度信號分解,EMD無法分解密集的頻率,即分解完的模態分量(IMF)含有多個實際模態頻率在里面,從而造成所萃取的瞬時頻率不規則。為克服這種現象,文獻[10]提出了一種改進的HHT方法,該方法首先利用FFT和帶通濾波器,將實際結構響應通過帶通濾波器分解成多個窄帶信號,最后再利用Hilbert變換把信號在時頻域上展現出來。本文分析采用該改進的HHT法。
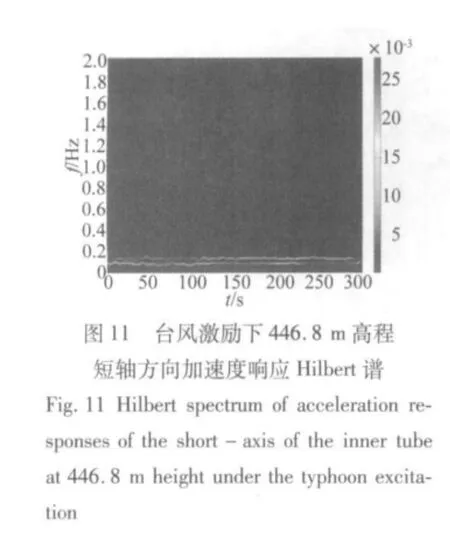
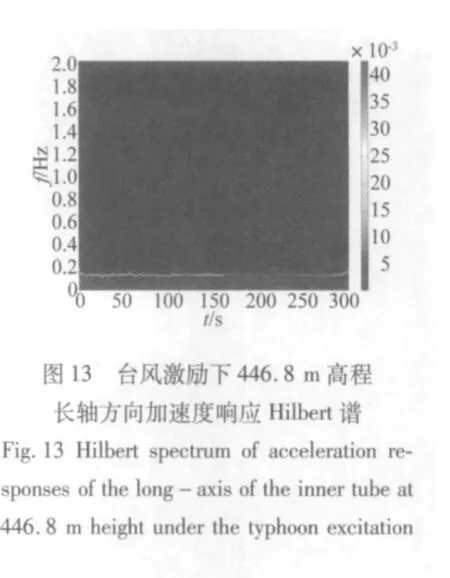
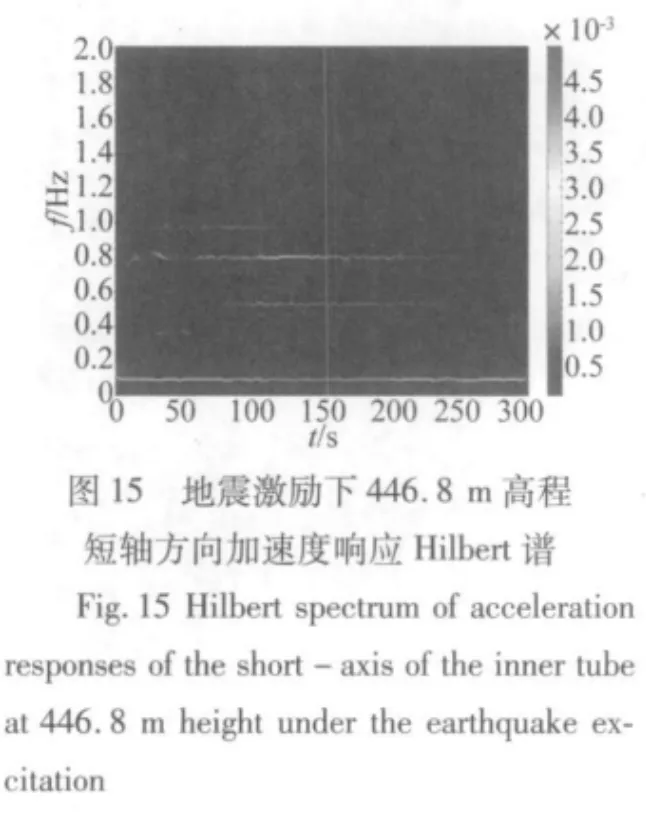
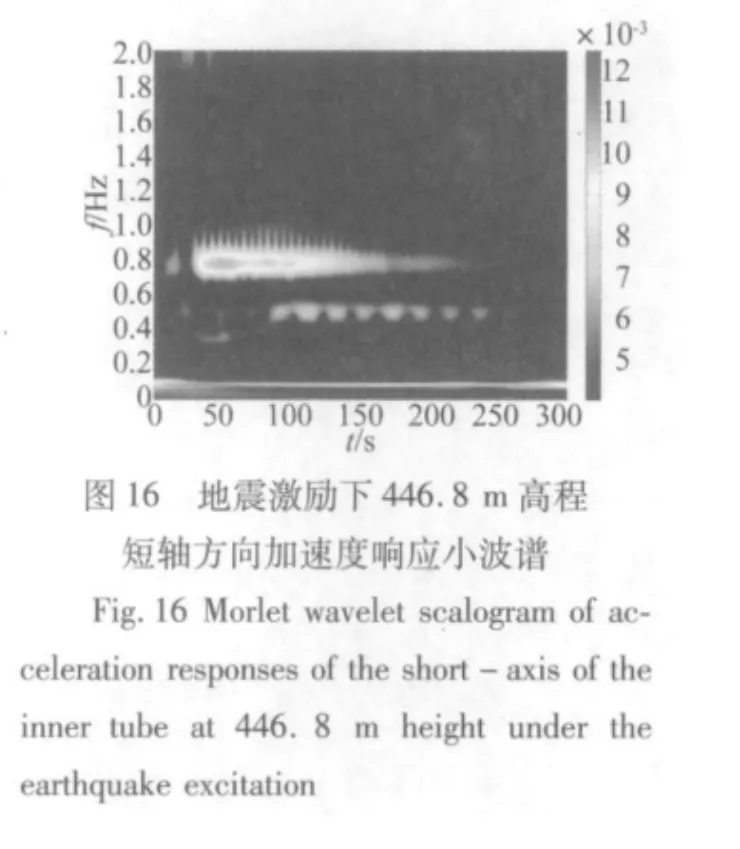
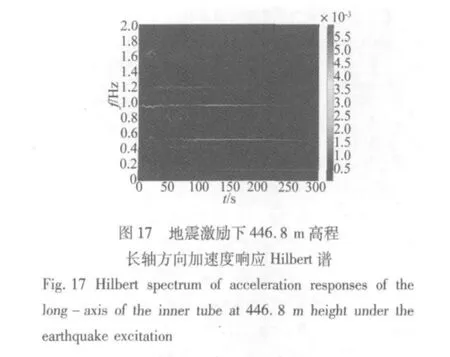
結構對不同時頻特性的激勵其響應特性是不同的。圖12至圖18所示為廣州新電視塔446.8 m高程加速度響應在臺風激勵和地震激勵下的Hilbert譜和小波譜。首先對比同個振動信號的Hilbert譜和小波譜,兩者都能大致描述結構響應的能量隨時間的變化情況,然而Hilbert譜能夠很清晰的反應結構的瞬時頻率隨時間的變化,小波譜只能大概反映結構能量隨時間的變化情況。進一步比較不同激勵下結構能量隨時間的變化情況,在臺風激勵下,結構的響應在時間上主要表現為最低的兩個模態頻率,而在地震激勵下,結構的響應主要表現為0.8 Hz和1 Hz左右兩個模態頻率,并且隨著地震激勵的減弱而逐漸減弱,同時在0.5 Hz左右也有一些能量分布,在地震激勵的同時結構也受一般風荷載的激勵,所以結構在時間上還一直表現出最低0.1 Hz左右的模態頻率。
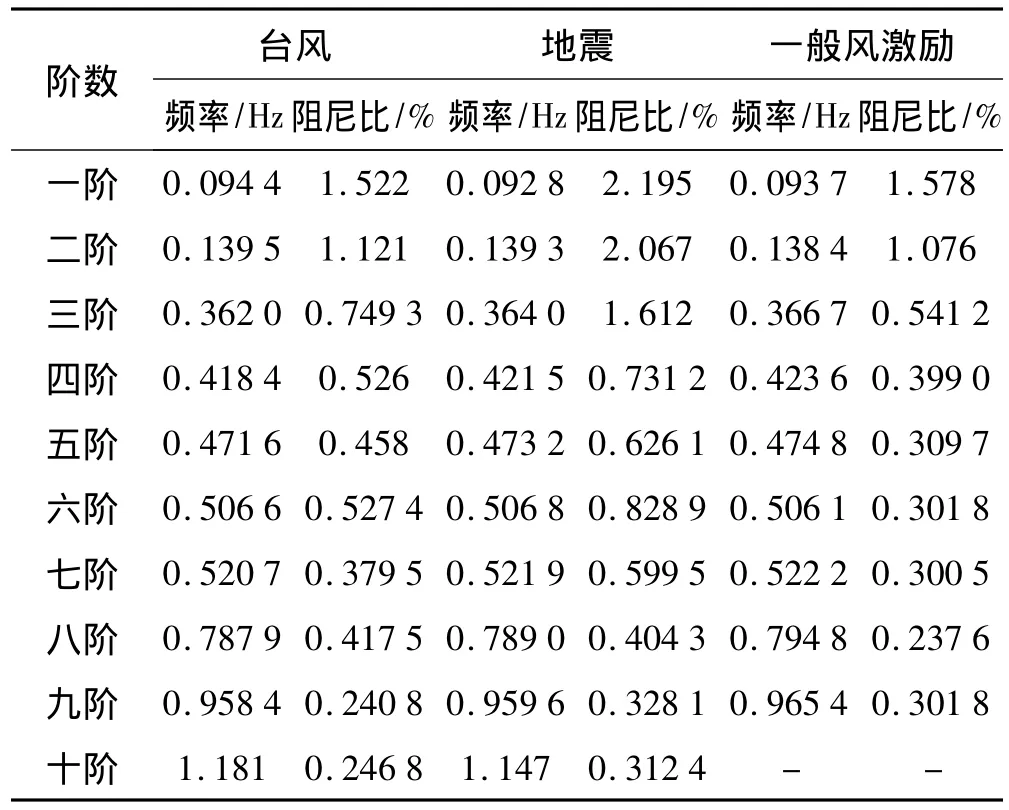
表1 不同激勵下模態頻率和阻尼比識別結果比較Tab.1 Comparison of modal frequency and damping ratio under different excitation condition



5 結論
本文以廣州塔為背景,介紹了其結構健康監測系統中的振動測試子系統,識別了結構在不同激勵下的模態參數,并利用時頻分析方法獲得結構在不同激勵下的動力特性,可以得到以下結論:
(1)不同激勵下結構的模態參數略有不同,這可能與輸入的激勵有關,也可能與環境因素(如溫度、濕度等)有關。
(2)結構在不同激勵下都呈現出密頻并且多模態耦合的形態,但是在不同激勵下結構最顯著的模態頻率不同。在臺風激勵下,結構的加速度風振響應以最低兩階頻率為主。在地震激勵下,結構的加速度地震響應以0.8 Hz和1 Hz兩個頻率為主。在一般風荷載激勵下,結構以較低幾個頻率為主。
(3)Hilbert譜和小波譜兩者都能大致描述結構響應的能量隨時間的變化情況,然而Hilbert譜能夠很清晰的反應結構的瞬時頻率隨時間的變化,小波譜只能大概反映結構能量隨時間的變化情況。
[1]陳偉歡,梁 碩,呂中榮,等.超高聳結構臺風期間動力特性監測[J].振動與沖擊,2010,29(6):15-20.
[2]Ni Y Q,Xia Y,Liao W Y,et al.Technology innovation in developing the structuralhealth monitoring system for guangzhou new TV tower[J].Structural Control and Health Monitoring,2009,16(1):73-98.
[3] Xia Y,Ni Y Q,Ko J M,et al.ANCRiSST benchmark problem on structural health monitoring of high-rise slender structures-phase I:field vibration measurement[C].Proceedings of the 5th International Workshop on Advanced Smart Materials and Smart Structures Technologies,USA,Boston,2009:30-31.
[4]Brincker R,Zhang L,Andersen P.Modal identification from ambient responses using frequency domain decomposition[C].Proceedings of the 18th International Modal Analysis Conference,San Antonio,Texas,USA,2000,4062(2):625-630.
[5] Gentile C,Saisi A.Ambient vibration testing of historic masonry towersforstructuralidentification and damage assessment[J].Construction and Building Materials,2007,21(6):1311-1321.
[6]He X F,Moaveni B,Conte J P,et al.System identification of alfred zampa memorial bridge using dynamic field test data[J].Journal of Structural Engineering,ASCE,2009,135(1):54-66.
[7]Li Q S,Wu J R.Time frequency analysis of typhoon effects on a 79-storey tall building[J].Journal of Wind Engineering and Industrial Aerodynamics,2000,95(12):1648-1666.
[8] Kijewski-Correa T,Kareem A.Efficacy of Hilbert and wavelet transforms for time-frequencyanalysis[J].Journalof Engineering Mechanics,ASCE,2006,132(10):1037-1049.
[9]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Journal of Proceedings of the Royal Society of London Series A,1998,454(1971):903 995.
[10] Yang W X.Interpretation of mechanical signals using an improved Hibert-Huang transform [J].Mechanical Systems and Signal Processing,2008,22(5):1061-1071.

