風振響應計算的新方法——廣義坐標合成法

陳 凱，符龍彪，錢基宏，金新陽

(中國建筑科學研究院，北京 100013)

風作用下的結構隨機振動一直是工程界關心的問題。通常認為作用于建筑結構表面的風荷載時程是完全隨機的平穩(wěn)過程。因此，結構物的風致響應習慣上根據(jù)經(jīng)典的線性結構隨機振動理論進行分析。以往的風振分析出于計算量的考慮，大多采用“平方－總和－開方”法，即所謂的SRSS方法，忽略了振型之間的耦合項。這種方法對于振型密集、阻尼很小的復雜結構會帶來較大誤差［1］。

目前應用最廣泛、準確度較高的算法是CQC完全二次型組合算法［2］。但CQC方法的計算比較繁瑣，對于復雜結構而言運算量極大。林家浩等［3］提出了“虛擬激勵法”用于隨機振動計算，在大幅縮減計算量的前提下獲得了與CQC完全等價的結果。該方法在風工程領域也已得到不少應用［4－6］。虛擬激勵法對給定激勵源頻譜特征的隨機振動較為有效。復雜結構的風振響應往往基于風洞試驗獲得的風壓時程進行計算，在運用虛擬激勵法之前，首先要進行功率譜估計，再進行譜矩陣分解，該過程的運算量仍然較大。謝壯寧［7－8］提出了風振分析的“諧波激勵法”，在對復雜結構進行風振分析時，相比傳統(tǒng)的CQC方法運算量和運算時間都有明顯改善。

虛擬激勵和諧波激勵本質上都是基于CQC完全二次型組合算法的改進，最終仍通過響應功率譜矩陣求解結構風振響應。

與此不同，本文提出了基于時程計算風振響應的廣義坐標合成法，通過廣義坐標的協(xié)方差矩陣求解響應統(tǒng)計值。該方法大幅減少了結構風振分析的計算規(guī)模和計算量，典型結構的計算規(guī)模和計算量不到CQC改進算法(諧波激勵法)的1/10，而通過該方法得到的風振響應的統(tǒng)計值與CQC方法完全等價，具有快速、高效、準確的特點。

另外，CQC的傳統(tǒng)和改進算法通常只能獲得響應的統(tǒng)計值。而若需獲得響應時程，則要進行極耗資源的時程分析。因而除了非常重要的工程之外［9］，很少被采用。這使得在進行關于背景響應與共振響應研究時，計算過程十分復雜［10］。而運用本文介紹的計算方法可以運用振型疊加直接得出風振響應時程，這為開展響應三分量分析(平均、背景、共振)和概率分析等研究創(chuàng)造了有利條件。

1 計算原理

1.1 CQC方法及其改進算法概述

建筑結構在風荷載作用下的運動方程可表示為:

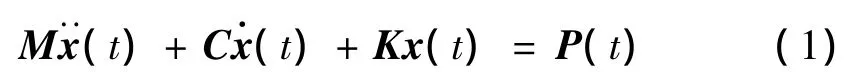
利用振型疊加法，取對質量矩陣歸一化的振型，可得出解耦后的廣義坐標運動方程:

其中fj(t)為第j階振型廣義力。根據(jù)隨機振動理論，可以推導出響應x(t)的功率譜密度為:

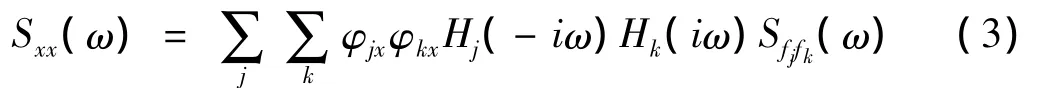
其中Hj為j階振型的頻率響應函數(shù)，［Sfjfk］為廣義力的功率譜矩陣，它可以用激勵力的譜矩陣表達，如下式:

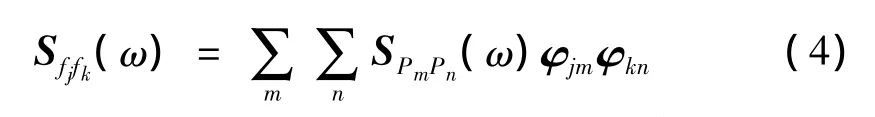
［SPmPn］是激勵力P(t)的功率譜矩陣。對響應的功率譜積分后，即可得出各點位移的方差。式(3)和式(4)就是所謂的CQC方法，若在求和過程中忽略交叉項則是SRSS方法。

當式(3)包含了全部振型時，該式得出的是精確解。在實際工程中，通常要進行振型截斷以減小計算量，計算時僅考慮結構的前若干階(通常不超過100階)振型。

虛擬激勵法針對式(3)的計算采用了改進算法，從而減小了CQC方法的計算量。而諧波激勵法的主要思路則是根據(jù)功率譜估計的周期圖算法，不直接計算激勵的功率譜矩陣，而是將相關項組合后，直接求得響應的協(xié)方差矩陣。其過程［7］簡述如下:

(1)對激勵力P(t)取傅里葉變換(實際上是快速傅里葉變換FFT)，得到P(ω);

(2)計算諧波激勵的頻率響應Y(ω)=Hs(ω)P(ω)，其中 Hs=ФHФT為結構頻響函數(shù)矩陣，這里的Ф是振型矩陣［φj］，H為振型頻響函數(shù)矩陣，該矩陣為對角陣，第j個對角元素為j振型的頻響函數(shù)Hj。

(3)根據(jù)功率譜的周期圖估計，響應的功率譜密度函數(shù)可表示為SYjYk=Yj(ω)Y*k(ω)/L(L為進行FFT計算的時點數(shù))，將響應功率譜密度矩陣求積分就可以得出響應的協(xié)方差矩陣。實際上，由于Y(ω)是N×L的矩陣(N為節(jié)點總自由度數(shù))，由矩陣乘法Y(ω)Y*T(ω)/L可直接得到協(xié)方差矩陣。

以上就是諧波激勵法的基本計算方法。諧波激勵法之所以能夠節(jié)約計算量，是因為它將Hs(ω)P(ω)作為一個整體來處理，避免了在計算激勵譜矩陣之后再做多次矩陣乘法。

1.2 廣義坐標合成法

結合風洞試驗進行的風振分析，激勵時程(即表面風壓時程)通常是已知的。針對這一特點，本文提出了廣義坐標合成法，根據(jù)振型疊加法和廣義坐標運動方程得出風致響應統(tǒng)計值。同時，對數(shù)據(jù)處理和計算過程進行了優(yōu)化，使計算規(guī)模主要由參與計算的振型數(shù)量決定，一定程度上擺脫了結構體系規(guī)模造成的計算瓶頸。

1.2.1 風振響應統(tǒng)計值的計算公式

由振型疊加原理，結構的位移響應由下式表示:

而振型廣義力則表示為:

對式(5)取時間平均，可得出響應平均值:

扣除平均量后，對式(5)進行矩陣乘法，可得:

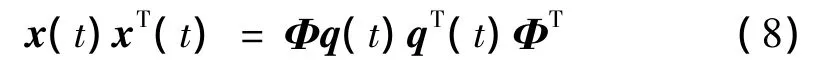
對式(8)求取數(shù)學期望，即可得:

其中Vxx和Vqq分別是響應和廣義坐標的協(xié)方差矩陣。Vxx的對角元即為對應響應的自方差，而其他元素則為不同響應之間的協(xié)方差。式(9)是廣義坐標合成法的核心公式，它通過振型的廣義坐標統(tǒng)計值的合成得出節(jié)點響應統(tǒng)計值。由于Vqq的階數(shù)與振型階數(shù)相同，用上式計算響應均方根非常方便快捷。

1.2.2 廣義坐標協(xié)方差矩陣Vqq的計算

當隨機振動問題由激勵功率譜矩陣刻畫時，Vqq可通過功率譜矩陣的頻域積分得出。而對于具備風洞試驗數(shù)據(jù)的風振問題，Vqq可通過對時程統(tǒng)計得到。這需要對廣義坐標運動方程，即式(2)進行求解。

式(2)為單自由度方程。該方程可在時域和頻域求解。時域的求解可采用杜哈梅積分方法，而頻域的求解則可借助傅里葉變換。對于連續(xù)時間系統(tǒng)，fj(t)通常不滿足平方可積條件，因而不能直接對式(2)兩端施以傅里葉變換。但由于風洞試驗得出的是有限個離散數(shù)據(jù)點，因此運用單自由度運動方程的頻域數(shù)值分析方法［11］，可利用快速傅里葉變換FFT對方程求解。從而廣義坐標的時程可由下式得到:

其中F+{}和F－{}分別表示快速傅里葉正變換和逆變換。在得到各階振型的廣義坐標時程后，即可根據(jù)Vqjqk=∑qj(t)qk(t)/L計算其協(xié)方差矩陣。求和號表示對所有離散時間點求和。

1.2.3 其他風振響應的計算

式(9)給出了節(jié)點位移響應協(xié)方差矩陣的計算公式。對于其他可由廣義坐標線性疊加得出的響應，也可仿照式(9)的推導過程得出其方差計算公式。假定響應r可用下式表示:

其中AT為行向量，其第j個元素Aj為j階振型對r的貢獻。由A的定義可知，振型矩陣只是A的一種特殊形式。易知r的方差可由下式計算:

對于速度和加速度等響應，無法通過廣義坐標的疊加獲得，但注意到:

因此，可首先計算廣義坐標的加速度時程，再根據(jù)式(13)得出節(jié)點加速度時程響應。利用FFT特性，j階振型的廣義坐標加速度時程可通過下式計算:

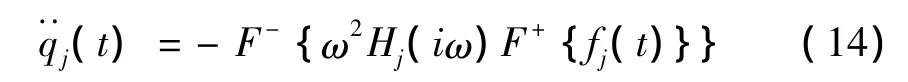
1.3 風振響應計算的前處理與后處理

1.2節(jié)建立了廣義坐標合成法的基本計算框架。但是，風洞試驗得到的壓力時程僅分布在少數(shù)測點上，需首先將其作用于所有結構受風節(jié)點。由此得出的結構激勵力P(t)包含了N個行向量，每個向量均有L個時程點的數(shù)據(jù)。由P(t)直接計算廣義力，計算量非常大，需要進一步的優(yōu)化。

1.3.1 廣義力時程的計算

式(6)給出了廣義力的計算公式。在一般的風振分析中，經(jīng)常將測點的風荷載時程直接作為集中力加載于距離最近的節(jié)點上，這種處理方式對于結構剛度分布不均勻的體系而言誤差很大。更為合理的方法是將測點的風荷載時程通過不同的插值方法作用于所有受風節(jié)點。本文采用了反距離加權方法計算節(jié)點風荷載。其公式為:

其中wk(t)為測點k的壓力時序，而lkj為結構受風節(jié)點j與測點k的距離。式(15)的計算中，事先挑選離節(jié)點最近的3個測點進行插值。將式(15)以矩陣形式表示，并代入式(6)，得出:

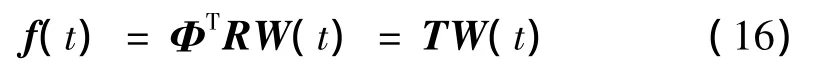
其中R為插值矩陣。根據(jù)本文所采用的插值方法，R為每行僅有3個非零元素的稀疏矩陣，T為最終轉換矩陣。利用式(16)可由測點壓力時程直接得出振型廣義力時程。因為T僅取決于結構振型和測點、節(jié)點的相對位置關系，因此只需要計算一次。且其為K×M階矩陣(K為振型數(shù)，M為測點數(shù))，比起直接用振型函數(shù)計算廣義力，減小的運算量相當可觀。1.3.2 背景響應與共振響應的計算

風振響應的平均分量、背景分量和共振分量可以由方程(1)的下述形式予以說明:

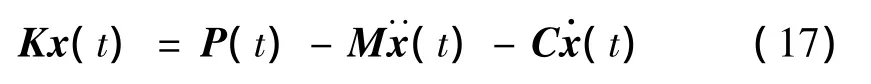
其中平均分量是由荷載的平均部分引起的響應。而在扣除平均荷載之后，式(17)右端第一項引起的響應即為背景分量。后兩項表示結構體系振動的附加力，由此附加力引起的響應，稱為共振響應。

廣義坐標合成法首先得出所有振型的廣義坐標時程，因而需要時可根據(jù)振型疊加法式(11)計算節(jié)點的響應時程，該時程包含了上述全部三個分量。

結構的平均響應和背景響應可分別由廣義坐標時程的對應分量給出。對應P(t)的廣義坐標時程可由下式得出:

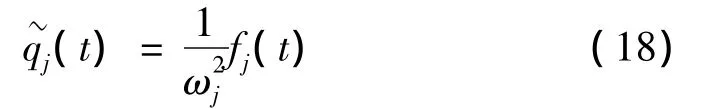
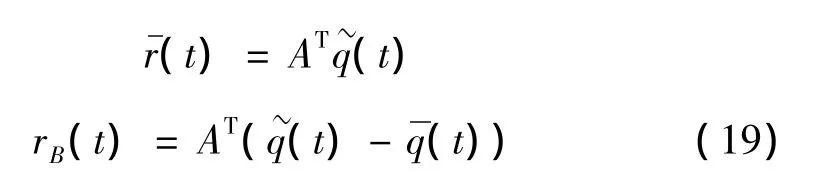
平均分量和背景分量之和通常也稱為準靜態(tài)響應。在得出響應中不同分量的時程后，即可求得響應的功率譜及其在時間上的概率分布，這為開展相關研究創(chuàng)造了便利條件。

1.4 廣義坐標合成法的深入討論

1.4.1 與CQC方法的等價性

廣義坐標合成法得出的結果與CQC方法的等價性，可結合式(12)和式(3)加以說明。對于某個特定的響應r(t)，其方差可由(9)式計算得:

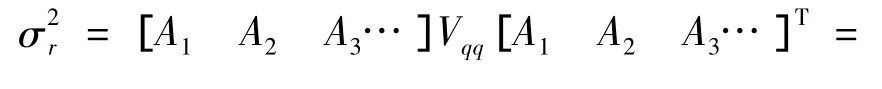
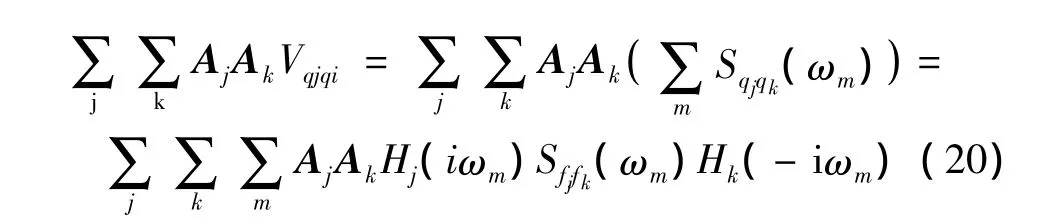
上式的推導過程中，在第三和第四步分別利用了帕斯瓦爾等式和廣義坐標與廣義力的頻域關系式。而根據(jù)CQC方法的基本公式，在利用式(3)求取響應均方根時，要對響應功率譜在頻域積分，離散情況下就是在信號頻譜范圍內(nèi)求和。如下式:

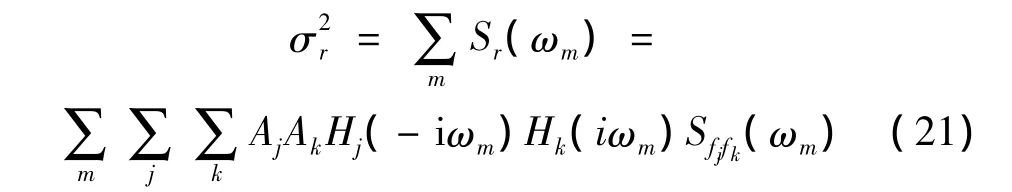
對比式(20)和式(21)即可發(fā)現(xiàn)，二者完全相同。這就證明了運用本文的廣義坐標合成法，得到的結果與CQC方法是完全等價的。

1.4.2 精度的討論

CQC方法需要先行估算譜密度矩陣。在結構風振分析中最常用的是周期圖方法，它是譜密度的漸近無偏估計。其估計的準確程度與采樣頻率和截斷長度有關，采樣頻率越高、截斷長度越長，準確程度越高，但相應的計算量就越大。由于廣義坐標合成法的計算公式與CQC方法是等價的，因此截斷長度和采樣頻率對這兩種方法也會產(chǎn)生相同的影響。

為了提高譜估計的準確程度，在CQC的計算過程中往往會采用加窗處理或者分段周期圖平均法。加窗處理是對原始時程數(shù)據(jù)進行了濾波，此時可以用濾波后的時程數(shù)據(jù)采用廣義坐標合成法進行計算，得出與CQC方法等價的結果;而分段周期圖平均法，相當于將廣義力時程劃分為若干對應段落進行計算最后取平均。簡言之，在CQC方法中采取的各種譜密度估計方法，都可得出與之等價的廣義坐標合成法，并由此得到與CQC方法完全等價的計算結果。

另一方面，根據(jù)單自由度運動方程的數(shù)值分析原理，由廣義坐標頻域求解公式得到的響應時程，實際上與時域采用差分法得到的時程等價，其精度也與時域差分的計算結果相同。

1.4.3 廣義坐標合成法的計算量和計算規(guī)模

本節(jié)將對廣義坐標合成法的計算量和計算規(guī)模進行估算。鑒于諧波激勵法是目前風振分析中計算速度最快、計算量最小的CQC算法，將對兩種方法進行比較。在此過程中，忽略了對計算量影響較小的因素。

設結構體系的受風節(jié)點總自由度數(shù)為N，風壓測點數(shù)量為M，每個壓力時序共有L個時點。計算過程共選取K階振型參與計算。表1給出了兩種算法的基本流程及其需要的乘法次數(shù)。

表1 兩種算法的主要步驟及所需乘法次數(shù)Tab.1 The counts of multiplication in the main steps of the two methods

除此之外諧波激勵法還需進行N次離散傅里葉變換(若對測點進行變換后再乘轉換矩陣則為M次)，廣義坐標合成法需要進行2K次離散傅里葉變換，一般情況下都會有M＞2K，因此忽略該因素不會高估諧波激勵法的計算量。另外在表1對諧波激勵法計算量的估算中，已經(jīng)考慮了 P(ω)=P*(－ω)對計算量的影響。

由于大多數(shù)情況下，N?L＞M＞K，因此諧波激勵法的計算量大致為N×L×N，而廣義坐標合成法的計算量大致由最后一步(N×K×K+N×K×N)所決定。考慮到這幾個量的大小關系，后者的計算量將會小很多。

而且在工程實踐中，往往并不需要得出不同節(jié)點響應的協(xié)方差。如果只計算節(jié)點的自方差，諧波激勵法仍然要計算出所有的Y(ω)，只是在最后一步減小了計算量。但廣義坐標合成法卻只需要式(20)計算N次。因此兩種方法所需計算量分別為N×N×L/2+N×L/2和N×K×(K+1)次。此時廣義坐標合成法的計算量更要小得多。

如果只需要對部分節(jié)點進行計算——比如只計算測點對應的M個節(jié)點自由度的響應——廣義坐標合成法最后一步所需乘法次數(shù)為M×K×K+M×K×M;而諧波激勵法為了得出同樣的結果，需要計算M個點的諧波激勵頻率響應，乘法次數(shù)M×N×L/2，計算響應統(tǒng)計值時，還需要再進行M×L×M/2次乘法。

為直觀比較兩種算法計算量的差別，取一種典型情況(受風節(jié)點自由度數(shù)N=30 000，壓力測點數(shù)M=1 000，時序點數(shù)L=2 000，振型K=100)進行了估算，并將結果列于表2。廣義坐標合成法的計算量包含了表1中的所有步驟。

表2 兩種算法對典型結構計算所需的乘法次數(shù)Tab.2 The counts of multiplication for a typical structure with the application of the two methods

可見，只要滿足N?L＞M＞K，廣義坐標合成法的計算量都要比諧波激勵法小得多。尤其是只需要計算響應自方差時，廣義坐標合成法所需計算量甚至比諧波激勵法低3個數(shù)量級。

廣義坐標合成法不但大大節(jié)約了計算量，對計算規(guī)模和內(nèi)存的要求也非常低。從表1可以看到，若完全按照矩陣乘法進行計算，諧波激勵法中的最大矩陣是Hs(ω)，它是N×N的方陣，即使稍小的Y(ω)，其階數(shù)也是N×L;而廣義坐標合成法的最大矩陣是振型矩陣Ф，其階數(shù)為N×K。以表2列舉的情況為例，兩種方法的最大矩陣所需內(nèi)存分別為120 MB和12 MB(已考慮Y(ω)的對稱性)，諧波激勵法的矩陣規(guī)模要比廣義坐標合成法高出一個數(shù)量級，這樣的差距對計算時間的影響相當可觀。當內(nèi)存開銷過大時，勢必要頻繁進行內(nèi)外存的數(shù)據(jù)交換，其耗費的時間甚至遠遠高于實際計算時間。

1.4.4 廣義坐標合成法實現(xiàn)高效計算的物理根源

從物理背景來考察，廣義坐標合成法之所以能夠減少計算規(guī)模、實現(xiàn)高效運算，是因為它并不直接求解物理空間變量的時域和頻域特征，而是將計算轉移到振型空間來進行。在得出廣義坐標的統(tǒng)計特征后，再由廣義坐標的統(tǒng)計特征合成物理空間所需統(tǒng)計值。

實際上在風振計算過程中，真正獨立的數(shù)據(jù)信息只有測點的風壓時程和結構的振型。因此，當把問題轉移到振型空間來分析時，自由度大大縮減，計算過程也不再包含冗余信息，計算規(guī)模自然就得以縮減。

比如用傳統(tǒng)CQC方法及其改進算法進行計算時，即使只需要求解1個點的響應，也必須考慮所有節(jié)點對該點的影響。也就是求一個Y(ω)也需要進行N×L/2次乘法。計算過程中有大量的冗余信息也參與了運算。當采用廣義坐標合成法求解時，這樣的冗余信息被全部過濾了，因此對計算量的縮減是不言而喻的。

2 算例分析

2.1 算例一:響應中不同分量的計算

針對一個大型火車站運用廣義坐標合成法計算其風振響應。風洞同步測壓試驗在中國建筑科學研究院的大型邊界層風洞中進行。風洞試驗段截面尺寸4 m×3 m。同步測壓點998個，采樣頻率400 Hz(換算到原型約 7.3 Hz)，采樣時間21 s。圖1為風洞試驗照片。

圖1 模型試驗照片F(xiàn)ig.1 Test model in wind tunnel

結構模型共有18 451個節(jié)點，其中受風面節(jié)點有8 981個。取600階振型進行分析。需要說明的是，車站第600階振型的自振頻率達7.1 Hz，超過了風洞測壓試驗的頻率分辨率，對于超出頻率分辨率的這些高階振型，計算結果只包括背景響應，基本沒有共振響應。但選取如此多的振型參與分析的主要原因是:在運用振型分解法進行風振分析時，結構的平均響應往往也通過振型疊加法獲得。由于大跨結構的特殊性，必須選取足夠多的振型才能得出較為精確的平均響應。其次，廣義坐標合成法計算效率非常高，即使選取的振型多達600階，計算速度也非常快。將某風向下的平均風荷載作用于結構模型上，并對靜力分析和振型分解法得出的節(jié)點位移進行了比較，選取前600階振型進行計算的精度已達95%以上。

采用廣義坐標合成法，計算測點對應節(jié)點的響應統(tǒng)計值(包括平均值、均方根和協(xié)方差)只需要4 s時間，計算所有受風節(jié)點的響應統(tǒng)計值也只需要10 s時間。文獻［8］中采用諧波激勵法進行響應計算，其計算規(guī)模遠小于本文(18 600個節(jié)點，270個測點，100階振型)，計算一個風向的響應所需時間約60 s。由此可見廣義坐標合成法的巨大優(yōu)勢。

根據(jù)式(11)計算了雨棚邊緣最大位移點(18 449號節(jié)點)的豎向位移響應時程，并根據(jù)式(19)計算了其準靜態(tài)響應時程，結果示于圖2。從圖2(a)中可明顯看到在準靜態(tài)響應之上疊加了較高頻率的共振響應。總響應的均方根為6.4 mm，而背景分量和共振分量則分別為 5.8 mm和 2.9 mm，二者相關系數(shù)接近 0(－0.001)。若采用傳統(tǒng)的CQC方法計算，背景和共振分量的計算過程將是相當繁瑣和復雜的。而由圖2(b)可見，背景分量反映的是脈動風荷載本身的頻譜特征，而總響應的功率譜中有4個峰值，分別對應4階不同的振型，可觀察到的被激起的最高階振型為第90階振型。

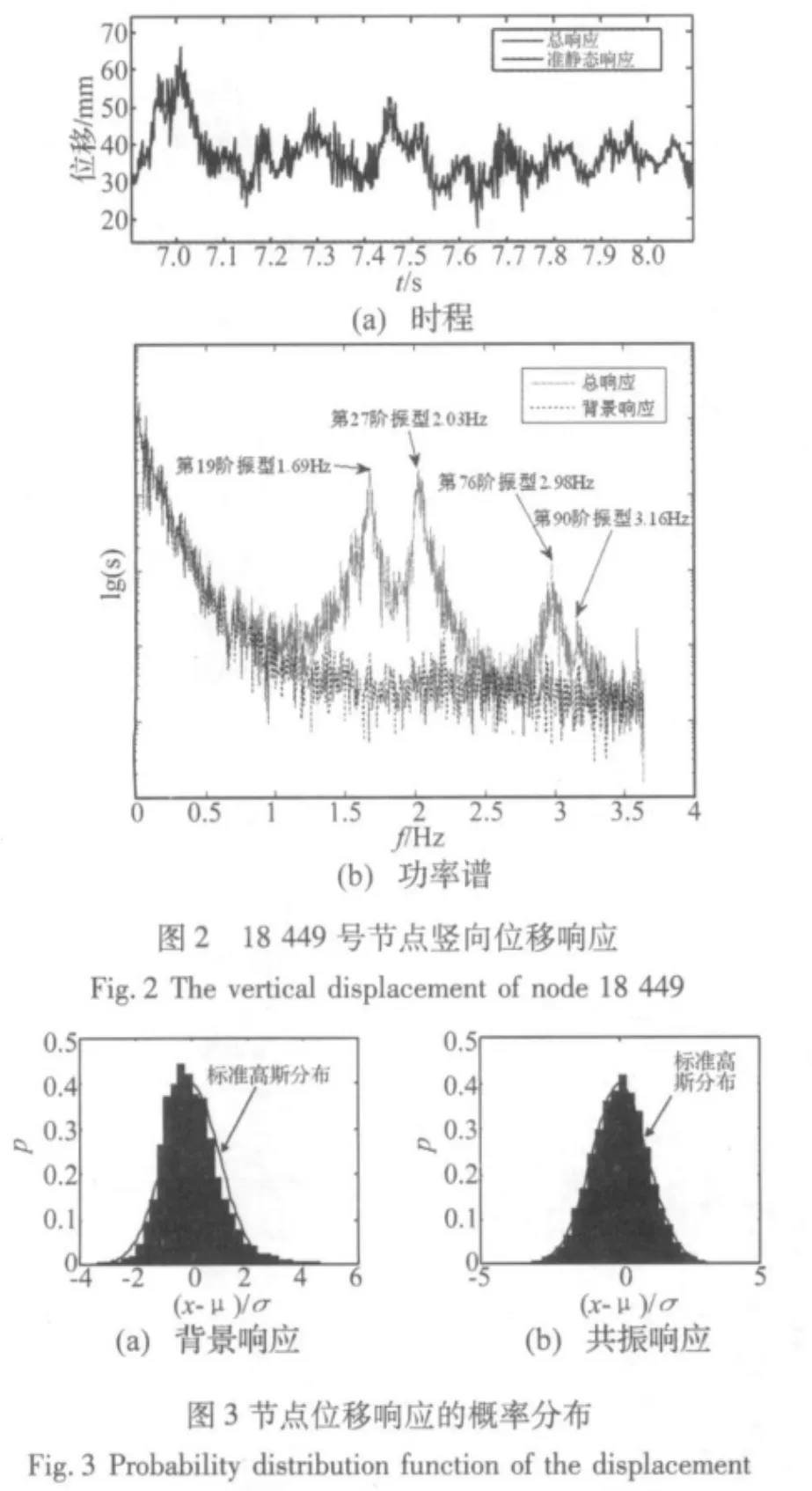
節(jié)點響應時程不但可以獲得響應的頻域信息，還可據(jù)此進行更多深入的分析。比如在計算極值響應時，多認為節(jié)點響應接近平穩(wěn)高斯分布，并據(jù)此選擇峰值因子進行計算。但以往大量研究表明大跨結構的脈動風壓時程的概率分布與高斯分布偏離較遠［12］。在這種非高斯的激勵源作用下，線性系統(tǒng)的響應時程也應當是非高斯的。

圖3分別給出了位移背景響應和共振響應的標準概率密度分布。可以發(fā)現(xiàn)共振響應的概率密度非常接近高斯分布，而背景響應的概率密度則有明顯的正向長尾。與高斯隨機過程的偏離，對于極值響應的估計有多大影響，是一個值得深入探討的問題。通過本文方法獲得的響應時程，為開展這類研究創(chuàng)造了有利條件。

2.2 算例二:加速度響應的計算

高層建筑在風荷載作用下的振動加速度涉及到舒適度問題，因而也是工程界所關心的。以往的風振分析，振動加速度的計算通常參照CQC方法首先計算加速度頻譜再積分。而根據(jù)式(13)和式(14)可以方便的得出加速度響應時程，且計算量也較小。

對某436 m高的超高層建筑進行了風洞同步測壓試驗，模型縮尺比1:450。結構前3階周期分別為7.96 s(y方向)、6.74 s(x方向)和4.13 s(扭轉)。利用廣義坐標合成法計算了該建筑的風振響應。圖4給出了在10年重現(xiàn)期風壓作用下，某風向角結構頂點的準靜態(tài)位移、總位移、速度和加速度信號。

由圖4(a)可見，位移、速度和加速度信號之間的相位差大致為180°，符合結構振動規(guī)律。準靜態(tài)位移并無明確的振動周期，而總位移則大致以結構在y方向的一階頻率振動。加速度信號除了可觀察到的低頻振動外，信號中還疊加了較高頻率的振動成分，反映了高階振型對加速度信號的影響更為顯著。這一現(xiàn)象在圖4(b)的功率譜中表現(xiàn)更為明顯，在加速度信號中，高頻分量所占的比例更高。

利用得出的加速度時程，可通過極值分析等方法得出結構頂點最大加速度，也可開展其他基于時程的分析研究工作。

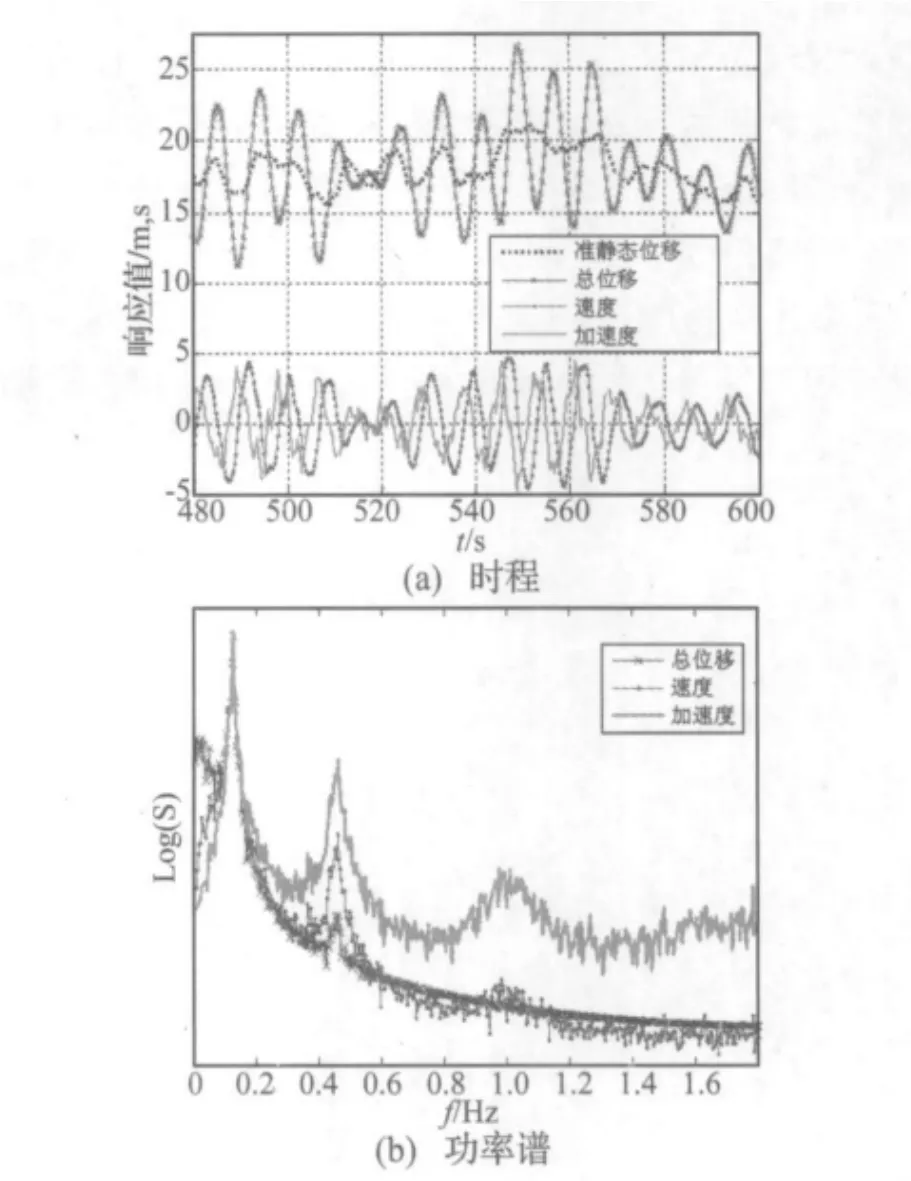
圖4 結構頂點響應Fig.4 Response at the structural top

3 結論

本文介紹了風振響應計算的快速算法——廣義坐標合成法。該方法針對風洞試驗中風壓時程為已知這一有利條件，首先利用快速傅里葉變換求解單自由度的廣義坐標運動方程，再通過時程統(tǒng)計得出廣義坐標的協(xié)方差矩陣，最后由該矩陣計算節(jié)點的響應統(tǒng)計值。對于加速度等不能由廣義坐標疊加而成的響應，則通過廣義坐標的加速度時程來計算。理論推導表明該方法得出的計算結果與CQC方法完全等價。

該方法的計算規(guī)模主要取決于參與計算的振型數(shù)量。由于通常情況下選取的振型數(shù)量遠遠小于節(jié)點數(shù)量，因此不但縮短了計算時間，而且由于大大降低了計算規(guī)模，使一般臺式機也可以開展大型結構的風振分析。對于只需得出響應統(tǒng)計值的問題，廣義坐標合成法的計算量和計算規(guī)模都不到CQC算法及其改進算法的1//10。尤其是當只求解響應自方差時，其所需計算量比CQC改進算法的小3個數(shù)量級。

廣義坐標合成法的另一個優(yōu)點是可以通過廣義坐標時程得出響應時程，為開展基于時程的分析研究提供了有利條件。

本文通過兩個實例計算證明了廣義坐標合成法的有效性。算例一是有上萬節(jié)點規(guī)模的結構體系，包含近千個測點和數(shù)百階振型，其每個風向角的響應統(tǒng)計值計算時間僅需數(shù)秒鐘;算例二則通過廣義坐標的加速度時程得出了高層建筑的頂部加速度響應時程，不同響應之間的計算結果符合結構振動的基本規(guī)律。實例分析中還給出了利用響應時程進行概率分析和功率譜分析得出的主要結果。

除了風振響應的計算之外，廣義坐標合成法可廣泛應用于各類已知激勵時程的隨機振動問題，實現(xiàn)高效、快速、準確地計算。

［1］ Wilson E L，Der Kiureghian A，Bayo E P.A replacement for the SRSS method in seismic analysis［J］.Earthquake Engineering＆ Structural Dynamics，1981，9(2):187－194.

［2］ 王國硯，黃本才，林穎儒，等.基于CQC方法的大跨屋蓋結構隨機風振響應計算［J］.空間結構，2003，9(4):22－26.

［3］ Lin J H.A fast CQC algorithm of PSD matrices for random seismic responses［J］.Computers and Structures，1992，44(3):683－687.

［4］ Xu Y L，Zhang W S，Ko J M，et al.Pseudo-excitation method for vibration analysis of wind-excited structures［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，83:443－454.

［5］ 陳賢川，趙 陽，董石麟.基于虛擬激勵法的空間網(wǎng)格結構風致抖振響應分析［J］.計算力學學報，2006，23(6):684－689.

［6］ 卜國雄，譚 平，張 穎，等.大型超高層建筑的隨機風振響應分析［J］，哈爾濱工業(yè)大學學報，2010，42(2):175－179.

［7］ 謝壯寧.風致復雜結構隨機振動分析的一種快速算法——諧波激勵法［J］.應用力學學報，2007，24(2):263－266.

［8］ 李小康，謝壯寧.大跨度屋蓋結構風振響應和等效靜風荷載的快速算法和應用［J］.土木工程學報，2010，43(7):29－36.

［9］ 田玉基，楊慶山.國家體育場屋蓋結構風振響應的時域分析［J］.工程力學，2009，26(6):95－99.

［10］ 陳 波，武 岳，沈世釗.背景響應、共振響應定義及其相關性分析方法［J］.振動工程學報，2008，21(2):140－145.

［11］ Clough R W，Penzien J.Dynamics of structures［M］.Computers and Structures，Inc，2003.

［12］ 葉繼紅，侯信真.大跨屋蓋脈動風壓的非高斯特性研究［J］.振動與沖擊，2010，29(7):9－15.