含初始彎曲裂紋轉子的振動分析

鄒 劍，董廣明，陳 進

(1.青島農業大學 機電工程學院，青島 266109;2.上海交通大學 機械系統與振動國家重點實驗室，上海 200240)

轉子系統是航空、電力、機械、化工、紡織等工業部門旋轉機械的關鍵性部件，隨著旋轉機械日益向高速、輕型、復雜結構、重載、大功率、長周期運行方向的發展，導致轉子的振動形態多變、應力狀態復雜、軸向溫度剃度分布過大以及工作介質的腐蝕加劇等，從而使轉子在運行過程中極有可能出現橫向裂紋并造成機毀人亡的災難性事故，因而有必要深入地研究裂紋轉子系統的動力學特性，利用現代振動測試與分析技術對轉子系統進行在線監測與故障診斷。

為計算轉軸橫向裂紋的柔度，將應變能釋放率理論與線性斷裂力學、轉子動力學相結合獲得較理想的結果;Papadopoulos［1］描述了應變能釋放率的基本理論與使用中的延伸與限制，給出了多種不同的裂紋識別方法。林言麗等［2］對現有裂紋轉子剛度模型進行了簡略的總結，提出了兩種原理不同、裂紋張開區域不同的確定剛度方法，試驗發現應力強度因子為零法能更好地反映裂紋轉子的剛度變化。Gasch［3］提出了簡單鉸鏈裂紋模型，將裂紋的張開與閉合狀態表示為方波函數，很好地描述了裂紋轉子周期變化的剛度及其穩定性，在裂紋轉子動力學建模和無損檢測中得到了廣泛的應用。冷小磊等［4］應用Monte-Carlo隨機模擬法，分析了白噪聲擾動下裂紋轉子剛度變化、轉速比等參數對系統分岔及混沌行為的影響，發現在擬周期與混沌解及其臨近的分叉參數區間，隨機擾動對系統響應有著較為顯著的影響，而周期解處則較小。DAI等［5］考慮了周期激勵作用下不對稱粘彈性支撐下的非線性裂紋轉子，采用 Floquet-Lyapunov理論研究了系統的線性、非線性動力穩定性，討論了不同因素對主不穩定區的影響。羅躍綱等［6］利用求解非線性非自治系統周期解的延拓打靶法和Floquet理論，研究帶有裂紋——碰磨耦合故障的具有三軸承支承的雙跨彈性轉子系統的周期運動的穩定性與失穩規律，認為雙跨裂紋轉子系統以倍周期分叉形式失穩，雙跨碰磨轉子系統以Hopf分叉形式失穩。

工程實際中，由于制造安裝誤差或運行中熱效應的原因，會使轉軸存在著一定的初始彎曲，進而導致轉子動撓度增加，機組的振動加劇，甚至引發轉子與靜子之間的碰磨。基于簡單鉸鏈裂紋模型，建立了含初始彎曲裂紋轉子的無量綱動力學模型;對比了含初始彎曲裂紋轉子與無初始彎曲裂紋轉子諧波頻率成分的差異，研究了系統的亞臨界共振特性，采用Floquet理論分析了含初始彎曲裂紋轉子的穩定性。

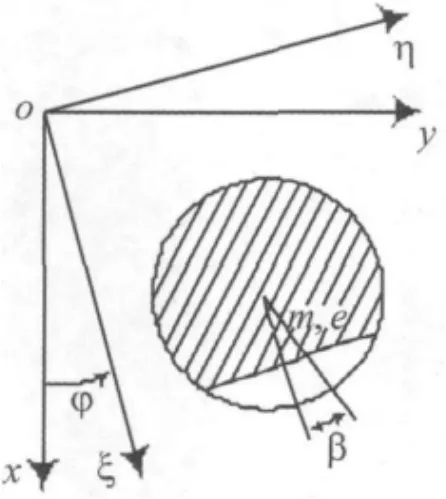
圖1 裂紋轉子橫截面Fig.1 Cross section of cracked rotor

1 動力學模型的建立

質量 m的 de Laval轉子，簡支于長L無質量的彈性軸上。假定，裂紋位于轉子的根部并且重力占優。建立圖1所示裂紋轉子的動力學方程:

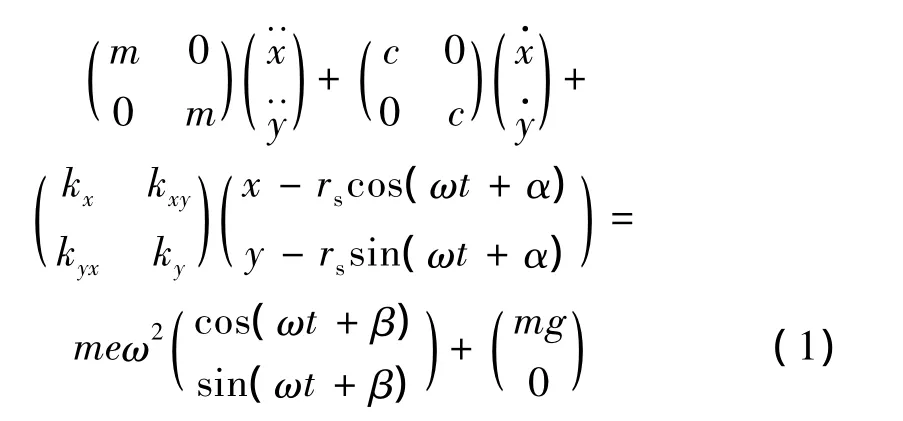
轉子的剛度矩陣為:

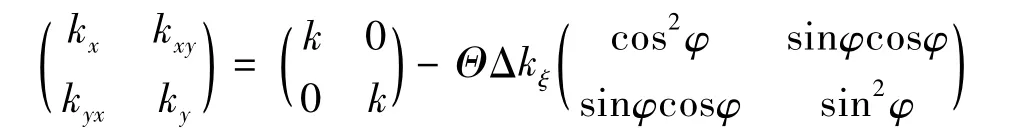
式中，對于勻變速裂紋轉子有φ=ωt。

裂紋開閉修正函數Θ可表示為［3］:

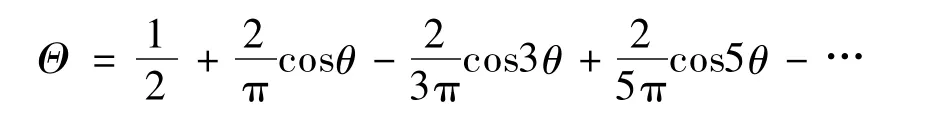
式中，θ=φ+β，研究中只考慮了級數的前四項。

令［x y］T=［Δx Δy］T+［xst0］T，在重力占優的情形下，式(1)轉變為;

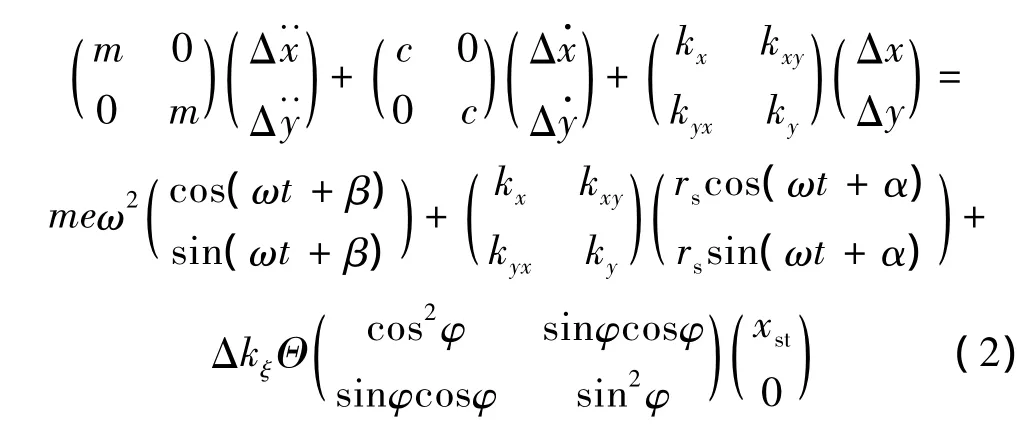
引入變量 τ=ωnt，Ω =ω/ωn，將式(2)轉變為無量綱形式:

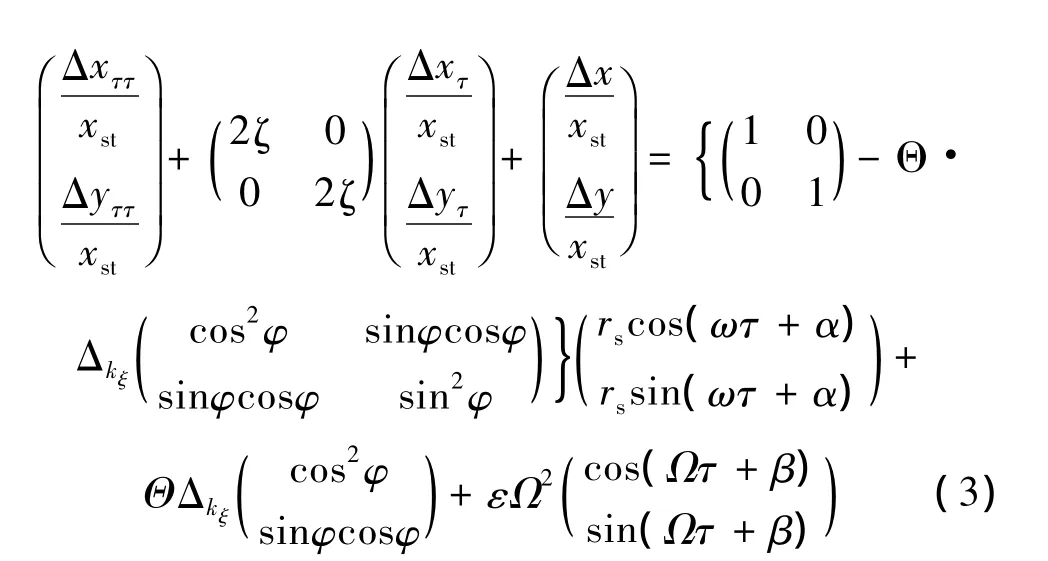
2 亞臨界共振

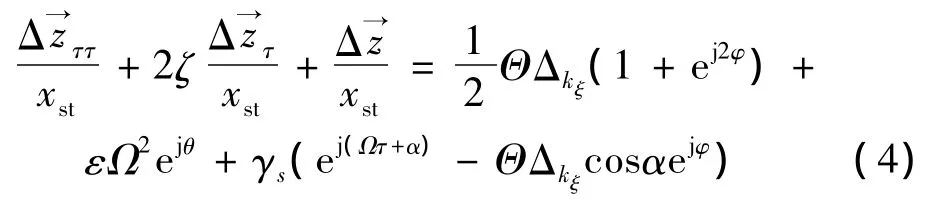
等式右邊各項依次為裂紋激勵、質量偏心激勵、與裂紋無關以及與裂紋相耦合的初始彎曲激勵。

將裂紋開閉修正函數Θ按歐拉方程展開，有:

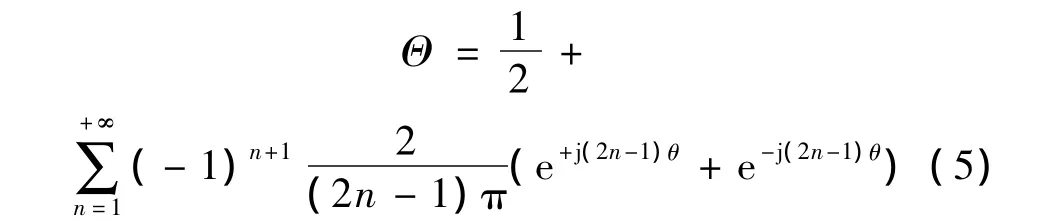
將式(5)代入式(4)，得:

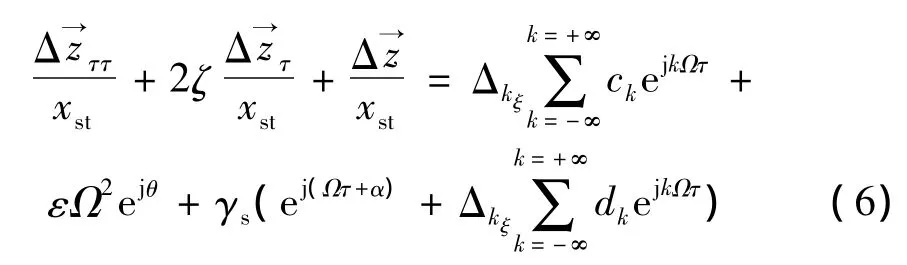
利用含初始彎曲裂紋轉子的解析表達式，可以對比無初始彎曲裂紋轉子與含初始彎曲裂紋轉子頻率成分的差異。無初始彎曲裂紋轉子僅僅存在著由裂紋引起的1，2，2n－1，…(n=2，3，4，…)等諧波成分，而含初始彎曲裂紋轉子則同時還存在著由初始彎曲導致的1，2，2n，…(n=2，3，4，…)等諧波成分。由于含初始彎曲裂紋轉子系統存在著1，2，n，…(n=3，4，…)等高次諧波分量，相應的必然存在著高次諧波的1/n(n=1，2，3，…)亞臨界共振。含初始彎曲裂紋轉子的1/2，1/3亞臨界共振的頻譜如圖2所示，可知在亞臨界共振時1次諧波分量占主導作用，而相應的高次諧波分量起著次之的作用。不考慮不平衡、直流分量以及與裂紋無關的初始彎曲激勵，令α=β=0，分別得到裂紋激勵、與裂紋相耦合的初始彎曲激勵各諧波分量的參與因子ck、dk，如表1與表2所示;可以看出:裂紋激勵與初始彎曲激勵的1，2次諧波的參與因子大于3，4次諧波的，并且正進動分量的參與因子大于反進動的。

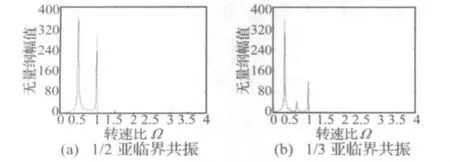
圖2 含初始彎曲裂紋轉子的頻譜分析Fig.2 Frequency spectra of cracked rotor with initial deflection

表1 裂紋激勵的參與因子Tab.1 Participation factor of crack excitation

表2 初始彎曲激勵的參與因子Tab.2 Participation factor of initial deflection

3 穩定性分析

為了研究含初始彎曲裂紋轉子的穩定性，考慮式(2)所示運動微分方程的齊次方程:

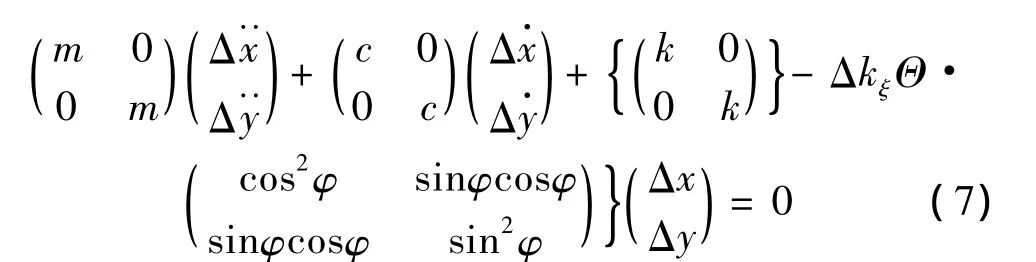
對式(7)進行無量綱化處理，得:

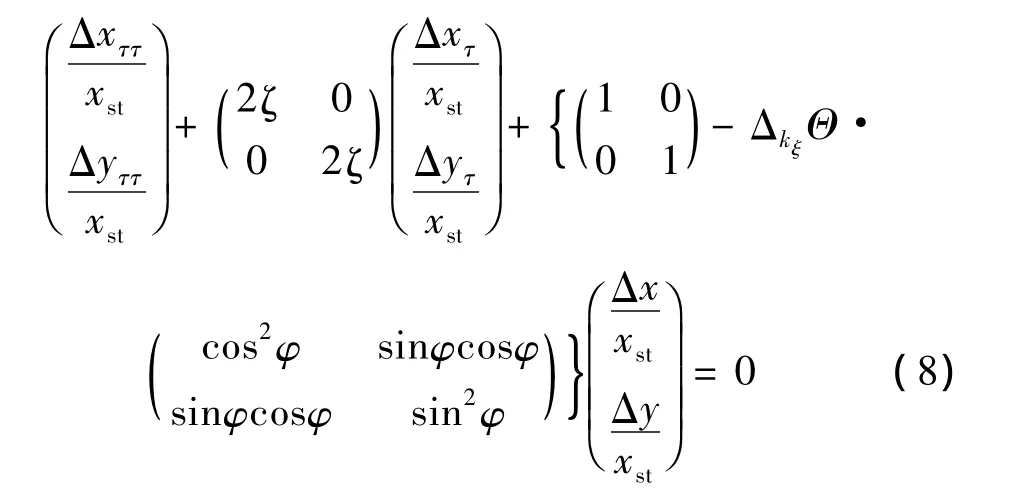
采用狀態空間表示法，式(8)改寫為:

式中，狀態矢量X為:

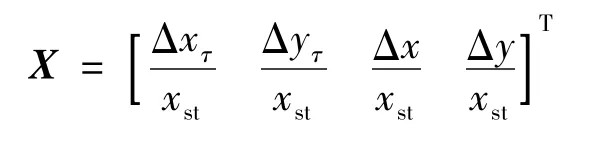
系統矩陣B為:

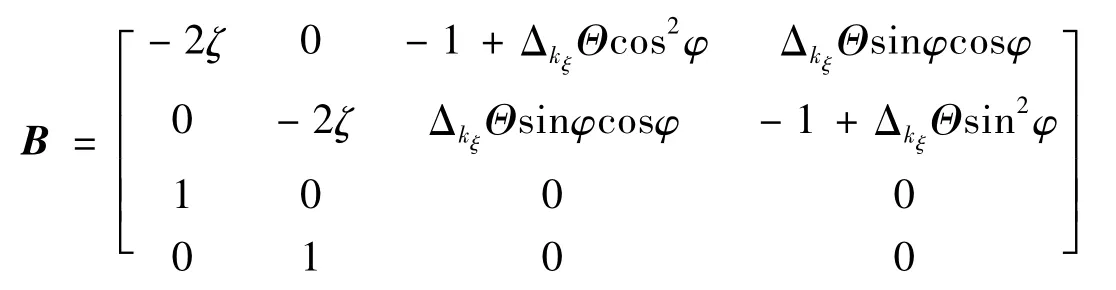
結合Floquet理論，可得:

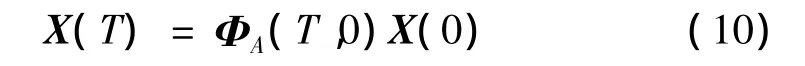
數值積分可計算得到含初始彎曲裂紋轉子系統的周期轉換矩陣 ΦA(T，0)。

為研究狀態矢量之間的關系，假定:

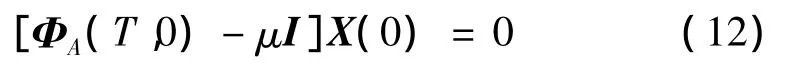
將式(11)代入式(10)，得到Floquet特征值問題:求解式(12)可得到周期轉換矩陣 ΦA(T，0)的特征值μ。

利用式(9)～式(12)可以研究含初始彎曲裂紋轉子的穩定性隨裂紋相對剛度變化Δkξ、轉速比Ω以及阻尼比ζ的變化關系，如圖3所示(圖中陰影部分表示轉速不穩定區)。由圖3可見，裂紋的存在導致轉子系統的穩定性發生變化，主要區別在于含初始彎曲裂紋轉子系統由單一不穩定轉速變為不穩定轉速區，并且不穩定轉速區的寬度隨著相對剛度變化Δkξ的增大而增加;阻尼則有抑制轉子系統不穩定的作用，隨著阻尼比ζ的增加不穩定轉速區變窄甚至消失。進一步深入分析圖3發現:在淺裂紋情形下，含初始彎曲裂紋轉子在轉速比 Ω =1/4，1/3，2/5，1/2，2/3，1，2 附近出現不穩定轉速區，并且不穩定轉速區在轉速比Ω=2/5，2/3，1，2附近比較明顯;而阻尼對于抑制轉子系統的不穩定作用顯著，即便是在小阻尼的情形下含初始彎曲裂紋轉子也僅僅在轉速比Ω=2/3，1，2附近出現不穩定轉速區。穩定性分析表明:當裂紋轉子系統啟停車時，必須保證較大的加速度才能通過參數不穩定轉速區(Ω=2/3)、主臨界不穩定轉速區(Ω=1)以及二次臨界不穩定轉速區(Ω=2)。

4 結論

(1)基于簡單鉸鏈裂紋模型，建立了含初始彎曲裂紋轉子的無量綱動力學模型。

(2)經解析求解對比了含初始彎曲裂紋轉子與無初始彎曲裂紋轉子諧波頻率成分的差異，發現系統存在著 1，2，n，…(n=3，4)等高次諧波分量，相應的必然存在著高次諧波的1/n(n=1，2，3，…)亞臨界共振。

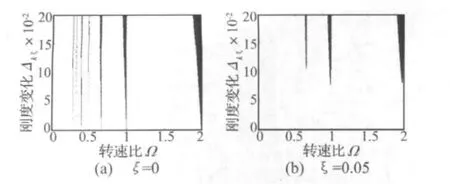
圖3 含初始彎曲裂紋轉子的穩定性Fig.3 Stability of cracked rotor with initial deflection

(3)采用Floquet理論分析了含初始彎曲裂紋轉子的穩定性，發現:在淺裂紋情形下，含初始彎曲裂紋轉子在轉速比 Ω =1/4，1/3，2/5，1/2，2/3，1，2 附近出現不穩定轉速區，并且不穩定轉速區在轉速比Ω=2/5，2/3，1，2附近比較明顯，而阻尼對于抑制轉子系統的不穩定作用顯著，即便是在小阻尼的情形下含初始彎曲裂紋轉子也僅僅在轉速比Ω=2/3，1，2附近出現不穩定轉速區。

附 錄

符 號

B——系統矩陣

c——阻尼

ck——裂紋激勵參與因子

dk——初始彎曲激勵參與因子

e——質量偏心

I——單位矩陣

k——無裂紋轉子的剛度

kx、ky——x、y 方向的彎曲剛度

kxy、kyx—— x、y 方向的交叉剛度

Δkξ——裂紋轉子ξ方向剛度變化量

Δk——剛度相對變化率ξ

rs——初始彎曲

X——狀態矢量

xoy——慣性坐標系

xst——靜態彎曲

T——周期

ω——角頻率

ωn——系統固有頻率

α——初始彎曲角

β——裂紋法向與質量偏心間的夾角

γs——相對初始彎曲

φ——轉角

ζ——阻尼比

Θ——裂紋開閉修正函數

ε——相對質量偏心

ΦA(T，0)——周期轉換矩陣

μ——特征值

下標 τ、ττ——對 τ的一階、二階導數

ξoη——旋轉坐標系

［1］ Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:a state of the art review ［J］.Mechanical Systems and Signal Processing，2008，22(4):763－789.

［2］ 林言麗，褚福磊.裂紋轉子的剛度模型［J］.機械工程學報，2008，44(1):114－120.

［3］ Gasch R.A survey of the dynamic behavior of a simple rotating shaft with a transverse crack ［J］.J.Sound and Vibration，1993，160(2):313－332.

［4］ 冷小磊，孟 光，張 韜，等.考慮隨機擾動時裂紋轉子系統的分叉與混沌特性［J］.振動工程學報，2006，19(2):212－218.

［5］ Dai L M，Chen C P.Dynamic stability analysis of a cracked nonlinear rotor system subjected to periodic excitations in machining［J］.Journal of Vibration and Control，2007，13(5):537－556.

［6］ 羅躍綱，聞邦椿.雙跨轉子——軸承系統裂紋——碰磨耦合故障的穩定［J］.機械工程學報，2008，44(4):123－127，132.