基于離散小波變換和Kalman濾波的直升機主減智能狀態預測

劉立生 ，楊宇航

(1.南京理工大學 自動化學院，南京 210094;2.總參謀部陸航研究所 可靠性室，北京 101121)

直升機主減具有傳動效率高、結構緊湊等特點，起減速、轉向及并車的作用。它將一臺或多臺高轉速小扭矩的發動機功率變成低轉速、大扭矩的功率傳遞給旋翼軸，并按轉速和扭矩的需要將功率傳遞給旋翼、尾槳及各個附件，以保證直升機正常工作。作為旋轉機械設備中的一種，主減常見故障類型有機器運行失穩、發生異常振動和噪聲、轉速發生變化等。Land［1］對HUMS(Healthy and Usage Monitoring Systems)進行研究;Samuel等［2］提出CBM+項目。這些項目的共同點是都對主減的狀態進行監控，從而減少了使用與保障(O＆S)費用，提高了直升機的安全性和維修效率。

振動信號常被用來對機械的故障進行診斷［3-4］，利用小波包變換［5-6］或者離散小波變換［7-10］對振動信號進行分解是兩種常用方法。在進行小波變換時，小波的選擇是關鍵，選擇不同的小波可能會得到不同的結果，Rafiee等［11］比較了324 種母小波，發現“db44”與振動信號最相似，分解效果最好。大量的研究是針對故障檢測進行的，而對故障進行預測的研究則相對比較少，文獻［12］對預測的方法進行了總結，包括五種方法:基于物理模型、人工神經網絡、先驗知識(專家系統、模糊系統)、統計方法(趨勢推斷、ARMA模型)以及隨機情況(Kalman濾波、Markov模型、Bayesian網絡、可靠性函數)。現實生活中設備受外界的干擾是隨機的，故對隨機情況進行研究更具有意義。Kalman濾波［13-17］通過一種算法排除可能的隨機干擾，提高檢測精度，能夠很好地對數據進行預測，廣泛應用于機器人導航、控制、傳感器數據融合以及軍事方面的雷達系統以及導彈追蹤等。

本文研究了離散小波變換、Kalman濾波以及Elman神經網絡組成的智能狀態預測系統。文中首先闡述了離散小波變換、Parseval定理、Kalman濾波以及Elman神經網絡等理論知識，在文獻［13］Kalman預測算法的基礎上提出了一種新的Kalman濾波預測算法，接著給出了主減智能狀態預測系統的預測流程圖，然后以某型直升機主減上8路振動傳感器采集的振動數據為例，去噪、分解，利用Parseval定理提取各層能量，分別使用這兩種Kalman濾波算法對各路傳感器各個時刻的特征向量進行預測，并用Elman神經網絡對預測值進行診斷，最終得出:本文提出的算法組成的智能狀態預測系統能夠更好地對故障進行預測。

1 基于離散小波變換的特征提取

函數ψ(t)∈L2(R)，其 Fourier變換(ω)滿足允許條件，則稱ψ(t)為一個基本小波或者母小波(mother wavelet)，將母小波經過縮放和平移之后，就可以得到小波序列(a，b∈R，a≠0)。給定基本小波函數ψ(t)，信號f(t)的連續小波變換為:

其中:a為尺度參數;b為平移參數。

對尺度參數a和平移參數b進行離散化處理，則離散小波變換為:

式中:a=2-j，b=n2-j。

離散小波變換可以實現多分辨率分析，它將信號分解為近似部分cAj小波系數和細節部分cDj小波系數，接著對近似部分進一步的分解，如此進行迭代，其分解如圖1所示，其J層分解表示為:

圖1 離散小波變換Fig.1 Discrete wavelet transform

離散小波變換各層能量的提取采用Parseval定理［18］:

式中:x(t)是時域信號，x(f)是離散信號的Fourier變換，N是采樣周期。把式(4)代入式(3)得:

2 Kalman濾波

Kalman濾波是以最小均方誤差估計為最佳準則來尋求一套遞推估計的算法，其基本思想是:采用信號與噪聲的狀態空間模型，利用前一時刻的估計值和現時刻的觀測值，用狀態方程和遞推方法來估計非平穩隨機信號的波形，求出現時刻的估計值。

考慮到直升機主減振動信號的特點，假設其狀態模型:

觀測模型:

式中:X(k)=［x(k)(k)］T，x(k)是k時刻的值(k)是x(k)在k時刻的變化率，Γ=［T2/2T］T，T為觀測周期，Z(k)是k時刻的測量值，H=［10］。w(k)和v(k)分別表示過程和測量的噪聲，假設為高斯白噪聲，協方差分別為Q，R。

定義:

(k|k-1):由k-1時刻的值估計(k);

P(k| k-1)k|k-1)對應的估計誤差協方差;

(k|k):k時刻的最優化估算值;

P(k| k)(k|k)對應的估計誤差協方差;

對目標進行Kalman預測具體的流程如圖2，實際中通常無法得到目標的初始值，常利用其前兩個觀測值建立初始估計，即:

進而得到初始估計的估計誤差:

從而得到初始估計誤差協方差:

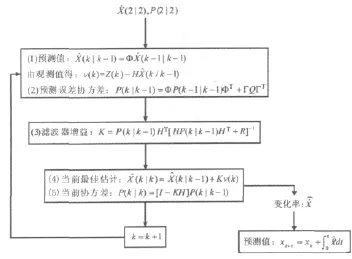
圖2 參數預測流程Fig.2 The flowchart of parameter estimation

在獲得變化率后，預測值使用得到，預測值有兩種算法:

(1)由初始兩個觀測值Z(1)，Z(2)，利用Kalman濾波求取不同時刻的變化率，獲得各時刻預測值［13］。

(2)由初始兩個觀測值Z(1)，Z(2)預測下一時刻的值(3)，用Z(2)與(3)構成新的觀測值，預測下一時刻值(4)，再用(3)與(4)構成新的觀測值，對下一時刻進行預測，如此反復迭代，從而獲得所有時刻的預測值，該算法是本文提出的方法。

為了簡潔起見，用“A”表示文獻［13］的算法，“B”表示本文的算法。

3 Elman神經網絡

Elman神經網絡由Elman提出，該模型在前饋網絡的隱含層中增加一個承接層，進行一步延時，達到記憶的目的，從而使系統具有適應時變特性的能力，能直接反映系統的動態特性。Elman型回歸神經網絡的結構如圖2，它一般由輸入層、隱含層、承接層和輸出層組成，，其中承接層也稱狀態層或上下文層，隱含層的輸出通過承接層的延遲與存儲，自聯到隱含層的輸入。這樣就使其對歷史數據具有敏感性，增加了網絡自身處理動態信息的能力，從而達到了動態建模的目的。

圖3 Elman神經網絡結構Fig.3 Structure of Elman neural network

4 主減智能狀態預測流程圖

基于上面介紹的理論，用 DWT、Kalman濾波和Elman神經網絡相結合構成直升機主減的智能狀態預測系統，其流程圖如圖4。

其具體過程為:使用振動傳感器采集直升機主減上的振動信號，去噪后進行離散小波變換，根據Parseval定理進行特征提取，提取的特征向量進行Kalman濾波由t時刻值預測t+τ時刻的值Xt+τ，最后經Elman神經網絡進行診斷。Elman神經網絡的診斷流程為:訓練數據是每一時刻由實測值獲得的特征向量;測試數據是Kalman濾波對應時刻的預測值，預測數據輸入訓練好的神經網絡進行故障診斷，從而實現對直升機主減的狀態進行智能預測。

圖4 主減智能狀態預測算法流程圖Fig.4 The workflow of MGB intelligent condition prediction algorithm

5 試驗驗證

振動傳感器監測直升機整個飛行過程中主減上各傳動齒輪及軸承處的振動水平，該振動傳感器是適用于直升飛機飛行試驗的ICP型傳感器，其工作溫度范圍寬，抗干擾能力強，數據采集設備采集8路振動信號，具體檢測部位和傳感器安裝位置如表1所示。

采集直升機地面試車其扭矩為10%時的振動數據，其初始采樣頻率為20 kHz，由于篇幅關系，以L001為例說明其具體過程。圖5為采集的L001信號，橫坐標為具體的飛行時刻，縱坐標為振動加速度，共有36 001 264個數據，它包括了一次飛行所有狀態下的振動數據，其包含的狀態太多，如:爬升、平飛、左側飛、俯沖、傾斜拉起等縱多飛行狀態。

表1 振動監測部位Tab.1 Location for vibration monitoring and measure

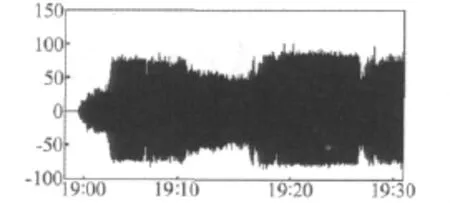
圖5 L001采集的原始信號Fig.5 Sample signals of L001

由于數據采集設備配套的FAMOS軟件實現不了像小波分析、神經網絡、Kalman濾波等復雜算法，但它可以對信號進行重新采樣，而Matlab軟件一次性處理不了采樣頻率為20 kHz的大量數據，故本文利用FAMOS軟件對各路振動信號進行重新采樣，然后利用Matlab軟件對新采樣后的信號進行分析。通過對各路信號進行重新采樣，使得采樣頻率為原頻率的1/20，即1 kHz，然后用語句:data1=Cut(L001，t1，t2)截取時間t1～t2之間的飛行數據，把這些數據拷貝到“.TXT”文檔中，供Matlab軟件調用。

選擇啟發式閥值對截取的信號進行去噪處理，對去噪后的信號使用Rafiee［11］中的“db44”進行離散小波分解，分解層數為9，每個傳感器得到10個特征向量，由于這10個能量數量級不同，如果直接輸入到Kalman濾波和Elman神經網絡中，容易產生誤判，故需用如下公式對其進行歸一化。

對Kalman濾波，分別采用A，B兩種算法對8路傳感器每個時刻的各個特征向量進行預測，預測的總時間為30 s，各個時刻的誤差采用如下公式:

其中，xi，j為第j個傳感器的第i個測量值;為第j個傳感器的第i個預測值;N為傳感器個數。

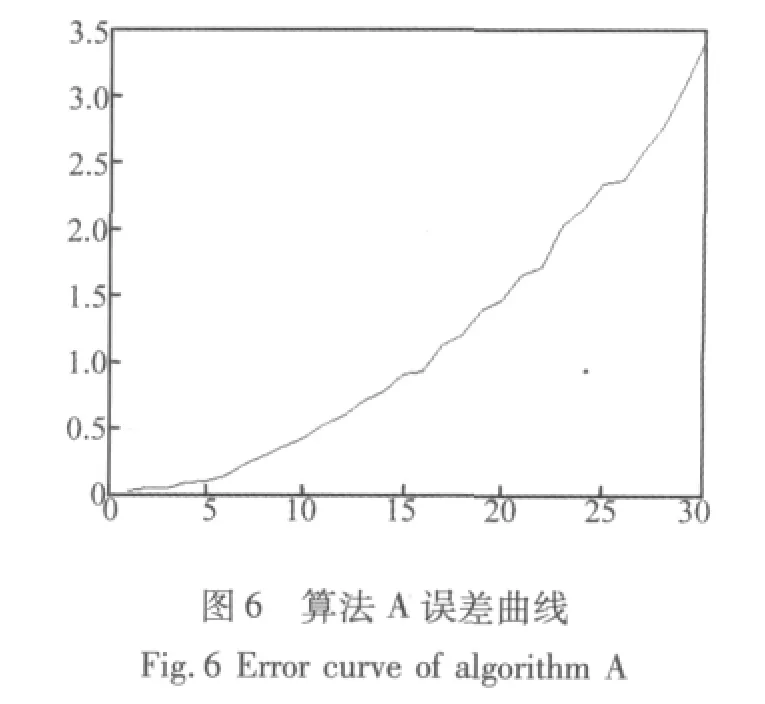
采用A算法時，各時刻誤差組成的誤差曲線如圖6，橫坐標為預測時間，縱坐標為誤差值，可以看出采用無迭代方法A時，預測時間越長，其對應的誤差就越大，而且誤差的變化率也在逐漸變大;采用B算法時，各個時刻對應的誤差曲線如圖7，可以發現隨著預測間隔的變大，誤差曲線上下波動，而不是單調上升。比較圖7和圖6，可以清楚地發現，相同時刻算法B的誤差值比算法A小得多，部分時刻的具體值如表2，通過表2和對應的圖可以知道，雖然圖7中波動比較大，但是它的縱坐標很小，從而說明算法B更適合于對各個時刻進行預測，它與實際測量值比較接近。

考慮主減常見的五種故障狀態:健康、運動失穩、異常振動、噪聲、轉速變化，分別用(1 0 0 0 0);(0 1 0 0 0);(0 0 1 0 0);(0 0 0 1 0);(0 0 0 0 1)表示。

為了研究Elman神經網絡各個時刻的逼近精度，選取健康狀態下的數據進行訓練和測試，未經過Kalman濾波的各個時刻的特征數據用于訓練神經網絡，經過Kalman濾波后獲得的預測值用來對網絡進行測試，使用newelm構建兩層Elman神經網絡，隱含層函數為tansig傳遞函數，輸出層為purelin傳遞函數，算法A與算法B部分時刻的逼近情況如表3所示，這里的逼近精度是相對于各個具體時刻的實際測量值而言的。

表2 不同預測時刻的誤差值Tab.2 Error value at different prediction horizons

表3 不同預測時刻神經網絡的逼近情況Tab.3 The approach accuracies of neural network at different prediction horizons

從上表可以看出，隨著預測時間的變大，算法A逼近精度在不斷地下降，如L008傳感器中，逼近精度在1 s時為 0.977 9，5 s時為 0.884 0，15 s時為0.690 7，28 s時為0.437 3;而 B 算法逼近精度相對都比較高，并且我們發現，隨著時間的推移，其相對逼近精度穩定在了一個值上。這進一步說明本文提出的算法更適合用于直升機主減智能狀態預測系統的構建。

6 結論

直升機主減是傳動裝置中結構最復雜、尺寸最大、重量最重的一個部件，它運轉的狀況直接影響著直升機的安全性和可靠性。針對其故障特點，文中提出了一種基于離散小波變換、Kalman濾波以及Elman神經網絡組成的直升機主減智能狀態預測系統，通過理論分析和實驗驗證得到如下結論:

(1)離散小波變換中，母小波選擇“db44”能很好地對信號進行分解，有利于應用Parseval定理對其各層進行特征提取。

(2)本文的 Kalman濾波預測算法更適用于對主減的特征向量進行預測，它能夠對8路信號的80個特征向量進行預測，并將各路特征向量的逼近精度穩定在一個比較高的固定值上。

(3)應用DWT、Kalman濾波以及Elman神經網絡構建直升機主減的智能狀態預測系統是可行的，有效的，它能對主減的狀態進行精確的預測，將為未來HUMS、PHM、CBM和CBM+系統的進一步開發提供新的技術參考。

［1］ Land J E.HUMS-the benefits-past，present and future［J］.IEEE，2001，6(s):3083-3094.

［2］ Samuel P D，Pines D J.A review of vibration-based techniques for helicopter transmission diagnostics［J］.Journal of Sound and Vibration，2005，282:475-508.

［3］Blunt D M，Keller J A.Detection of a fatigue crack in a UH-60A planetgearcarrierusing vibration analysis［J］.Mechanical Systems and Signal Processing，2006，20:2095-2111.

［4］Rafiee J，Rafiee M A，Tse P W.Application of mother wavelet functionsforautomatic gearand bearing fault diagnosis［J］.Expert Systems with Applications，2010，37:4568-4579.

［5］Wang D Y，Zhang W Z，Zhang J G，et al.Fault bearing identification based on wavelet packet transform technique and artificial neural network［J］.International Conference on System Science，EngineeringDesign and Manufacturing Informatization，2010，2(s):11-14.

［6］ Wu J D，Liu C H.An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network［J］.Expert Systems with Applications，2009，36:4278-4286.

［7］ Wu J D，Liu C H.Investigation of engine fault diagnosis using discrete wavelet transform and neural network ［J］.Expert Systems with Applications，2008，35:1200-1213.

［8］ Saravanan N，Ramachandran K I.Incipient gear box fault diagnosis using discrete wavelet transform(DWT)for feature extraction and classification using artificial neural network(ANN)［J］.Expert Systems with Applications，2010，37:4168-4181.

［9］Wu J D，Huang C K，Chang Y W.Fault diagnosis for internal combustion engines using intake manifold pressure and artificial neural network ［J］.Expert Systems with Applications，2010，37:949-958.

［10］ Wu J D，Kuo J M.An automotive generator fault diagnosis system using discrete wavelet transform and artificial neural network［J］.Expert Systems with Applications，2009，36:9776-9783.

［11］ Rafiee J，Rafiee M A，Prause N，et al.Application of mother wavelet functionsforautomatic gearand bearing fault diagnosis［J］.Expert Systems with Applications，2010，37:4568-4579.

［12］ Sikorska J Z，Hodkiewicz M，Ma L.Prognostic modelling options for remaining useful life estimation by industry［J］.Mechanical Systems and Signal Processing，2011，25:1803-1836.

［13］ Wu S L，Bechhoefer E，He D.A practical regime prediction approach for HUMS applications［J］.American Helicopter Society 63rd Annual Forum，Virginia Beach，VA，2007:1-8.

［14］Peel L，Driven D.Data driven prognostics using a kalman filter ensembleofneuralnetwork models ［J］. International Conference on Prognostics and Helth Management，2008:1-6.

［15］Lall P，Lowe R，Goebel K.Prognostics using kalman-filter models and metrics for risk assessment in BGAs under shock and vibration loads［J］. Electronic Components and Technology Conference，2010:889-901.

［16］ Carr M J， Wang W B. An approximate algorithm for prognostic modelling using condition monitoring information［J］.European Journal of Operational Research，2011，211:90-96.

［17］ Matej G，Dani J，Pavle B，et al.Model-based prognostics of gearhealth using stochastic dynamicalmodels ［J］.Mechanical Systems and Signal Processing，2010，25(2):537-548.

［18］ GaingZ L. Wavelet-basedneuralnetworkforpower disturbance recognition and classification ［J］. IEEE Transactions on Power Delivery，2004，19(4):1560-1568.