振動流化床與浸沒水平管平均傳熱特性理論分析與實驗研究*

朱學軍 ，鄧 俊

（1.攀枝花學院 生物與化學工程學院，四川 攀枝花 617000；2.攀枝花市化工資源有效利用重點實驗室，四川 攀枝花 617000）

流化床的一個顯著特征就是床層溫度均勻和具有較高的傳熱效率，這使它對于一系列的反應，特別是具有高放熱效率的放熱反應特別適應，同樣由于浸沒管表面可以向床內移入和移除熱量，所以在各工業部門中已獲得了廣泛應用。

在流化床內設置熱交換管束，管內通入蒸氣或其它加熱介質，利用管壁表面與流化床層間高的傳熱速率，向床內施加補充熱量，從而提高流化床干燥器的熱效率及干燥能力。通過浸沒表面提供的熱量可以占到總供熱的80%甚至更高，考慮氣體供熱和浸沒加熱管供熱的平均效率可達90%，從而熱能消耗可大大降低，可實現干燥過程得高效節能[1]。

近年來，關于流化床與浸沒水平換熱管的傳熱實驗研究非常活躍，在很多方面都取得了重大突破，這方面的專業文獻也很豐富[2-4]。但不同研究者所得出的計算式相差很大，而且各個關聯式適應范圍不同，即僅在各自的實驗條件下才能很好地相符合。由于影響流化床傳熱的因素很多，到目前仍沒有一個適用于整個流化床的傳熱關聯式。

關于振動流化床與浸沒表面的傳熱模型主要是通過固定式流化床與浸沒表面間的傳熱模型修正得來的。Ringer and Mujumdar認為對于傳統流化床傳熱系數在u＞umf后增加的原因是更有效的顆粒混和，而對于振動流化床的傳熱系數還強烈的依靠振動參數和顆粒直徑，在垂直振動的流化床中控制合適的振動參數和氣速就可以使床內顆粒流動和傳熱達到最佳，并在不振動流化床傳熱模型的基礎上得到了預測振動流化床傳熱系數的數學模型。

Pakowski et al通過實驗證實，振動對于細小顆粒與浸沒表面的傳熱系數具有較大的影響，能夠顯著增加傳熱系數，但對于大顆粒，這種影響的作用將減弱，甚至在某些情況下還會削弱傳熱，使傳熱系數反而下降。Mujumdar and Pakowski認為振動的引入，可以強化傳熱，在較低的通氣速度下即可獲得較大的傳熱系數，氣流速度僅在u＜umf時才對傳熱系數有較大影響，振動流化床最大傳熱系數比不振動大10%～20%。

Malhotra and Mujumdar以 dp=0.325～1.017mm的玻璃珠為物料，采用二維振動流化床，研究了振動頻率、振幅、氣速、顆粒直徑和顆粒濕含量等因素對床層與浸沒水平圓柱表面平均傳熱特性的影響。當振幅固定在4.25mm，u/umf＝0時，振動可以大大強化傳熱，表面與床層間傳熱系數可以提高超過20倍。

本研究以平均粒徑為1.83mm的玻璃珠為物料，研究了振動流化床與水平管間的傳熱規律；考察了氣速、振動頻率、靜床高度、管徑等因素對平均傳熱系數的影響。在顆粒團更新理論基礎上建立了顆粒團對流傳熱系數數學模型、氣體對流傳熱系數關聯式，從而得到振動流化床與浸沒水平管平均傳熱模型。比較了傳熱系數的理論預測值與實驗測定值，兩者吻合較好，從而驗證了提出的傳熱模型的正確性。

1 傳熱模型建立

對于振動流化床，由于機械振動的引入將影響床層顆粒的流化狀態。影響床層與浸沒表面間傳熱系數的因素還包括振動參數（振動頻率和振幅）。所以振動流化床與浸沒水平管間的傳熱比固定式流化床更加復雜，床層與浸沒表面間的傳熱系數可用式（1）表示

式中 f0：氣泡分率 /%；hpp、hgc、hb和 hr分別為顆粒團對流傳熱系數、氣體對流傳熱系數、氣泡傳熱系數和輻射傳熱系數，W·（m2·K）-1。

振動流化床顆粒床層與浸沒水平管表面傳熱物理模型見圖1[5]。通過建立物理模型可以得到顆粒團對流傳熱系數計算式和氣體對流傳熱系數計算式。

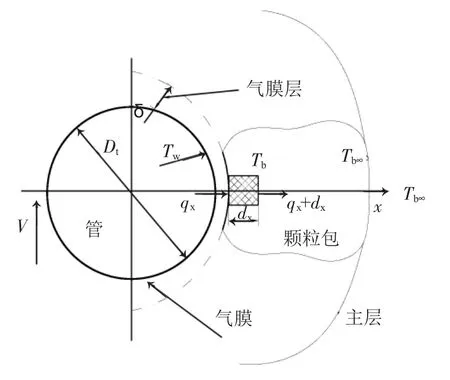
圖1 水平管傳熱物理模型Fig.1 The heat transfer model of horizontal tubes

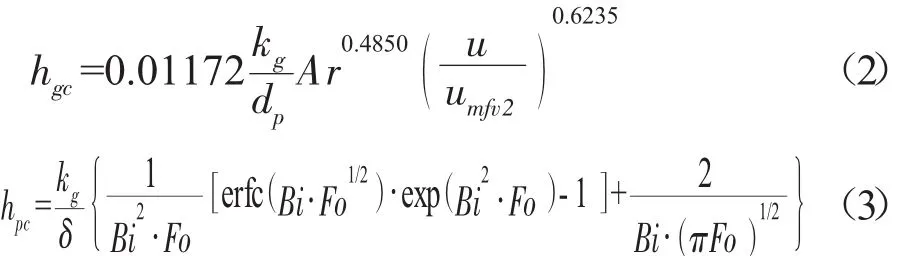
其中氣體對流傳熱系數由式（2）計算，顆粒團對流傳熱系數通過式（3）計算。管壁平均傳熱系數have可采用局部時均傳熱系數的面積平均來計算。

2 傳熱特性實驗裝置及原理

圖2為振動流化床傳熱特性實驗裝置示意圖。實驗用振動流化床為240×80mm2的二維流化床。為便于觀察床內物料運動狀態，床體由透明有機玻璃制成。分布板采用開孔率為4.9%、孔徑為2mm的多孔板。其上鋪設一層100目的不銹鋼絲網以使氣流均布，振動流化床床體通過四根金屬彈簧支撐在固定支架上，床體通過導向連桿與一偏心機構相連接，偏心裝置通過皮帶與調速電機相連。借助偏心裝置的作用，將電機的旋轉運動轉換成床體在豎直方向上的往復運動。導向連桿上裝有直線運動軸承，保證床體僅沿豎直方向運動，克服水平方向上的擺動。振幅可通過改變偏心距來調節，振動頻率則通過調節調速電機的轉速加以控制，并通過數字式光電轉速表測出。氣體由鼓風機通過孔板流量計計量后由床底進入。

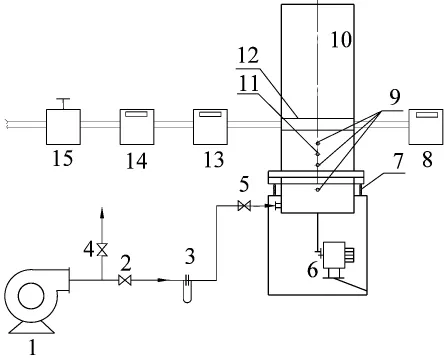
圖2 平均傳熱系數測試實驗裝置示意圖Fig.2 Schematic diagram of the experimental system

測量傳熱系數的水平管如圖3所示。在直徑25 mm、長60 mm的銅棒同心嵌入一長為60 mm，直徑為4 mm的加熱棒，棒體兩端用聚四氟乙烯端頭封住，在銅體表面焊接銅－康銅熱電偶，熱電偶引線從表面內側穿過端頭引出。水平管兩端固定在床壁上。水平管軸線距氣體分布板60 mm，對稱安裝在床的中心位置，床層溫度由安裝在水平管下方距氣體分布板20 mm處的裸露熱電偶測定。實驗時，將流化氣速調節至一定值，并使流化床按一定的振幅和頻率進行振動，接通加熱電源，實驗持續到微元面的溫度穩定不變時，測得微元管壁溫度和床層溫度，即可按式（5）計算平均傳熱系數h。

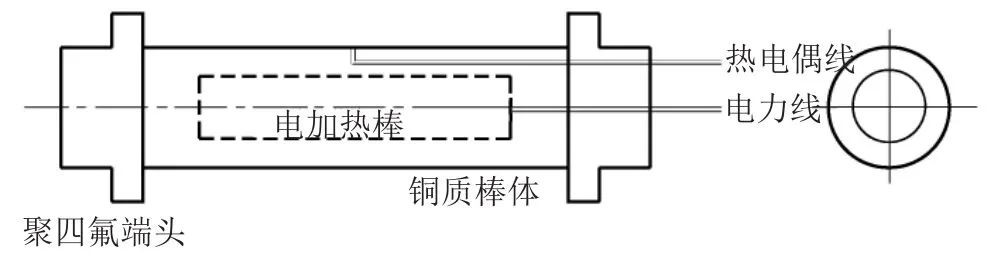
圖3 平均傳熱系數測試探頭Fig.3 Test probe of the average heat transfer coefficient

式中 h：傳熱系數，W·（m2·K）-1；Q：通入水平管的熱量，J·s-1；A：水平管測試部位面積，m2；tw：管壁溫度，℃；tB：床層溫度，℃。

3 結果與分析

3.1 振動頻率的影響

圖4、5比較了水平管直徑為25mm，床高為95mm時不同振動頻率和流化氣速的條件下平均傳熱系數理論預測值與實驗測定值之間的關系。

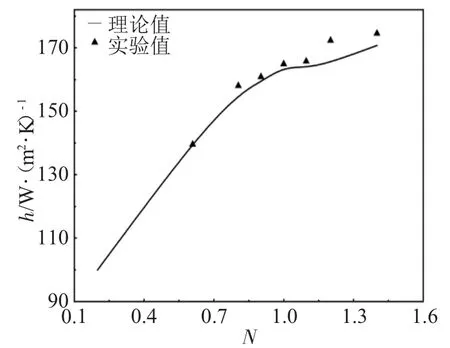
圖4 平均傳熱系數理論計算值與實驗值的比較Fig.4 Comparison of experimental values of the average heat transfer coefficient with calculated values（f=6.7Hz,H0=95 mm）

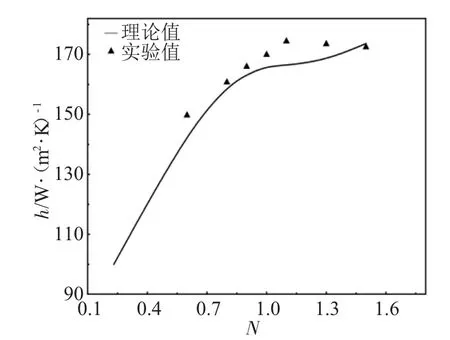
圖5 平均傳熱系數理論計算值與實驗值的比較Fig.5 Comparison of experimental values of the average heat transfer coefficient with calculated values（f=11.2 Hz,H0=95 mm）

從圖4、5中可以看出，實驗值和理論預測值雖有差異，但差別較小。在各種振動頻率下流化數較小時理論預測值和實驗值吻合較好；在較高流化數、低振動頻率時，實驗值處于理論值上方；隨著振動頻率增大，平均傳熱系數實驗值逐漸趨于理論預測值甚至低于理論預測值。這主要由于振動頻率和流化數大時，床內氣泡分率增加，所以傳熱系數降低，但理論預測值中假定氣泡傳熱與氣體傳熱系數相當，所以預測值偏大。

3.2 床高對平均傳熱系數的影響

圖6比較了水平管直徑為25mm、床高為130mm、振動頻率為11.2Hz的條件下平均傳熱系數理論預測值與實驗測定值之間的差異。

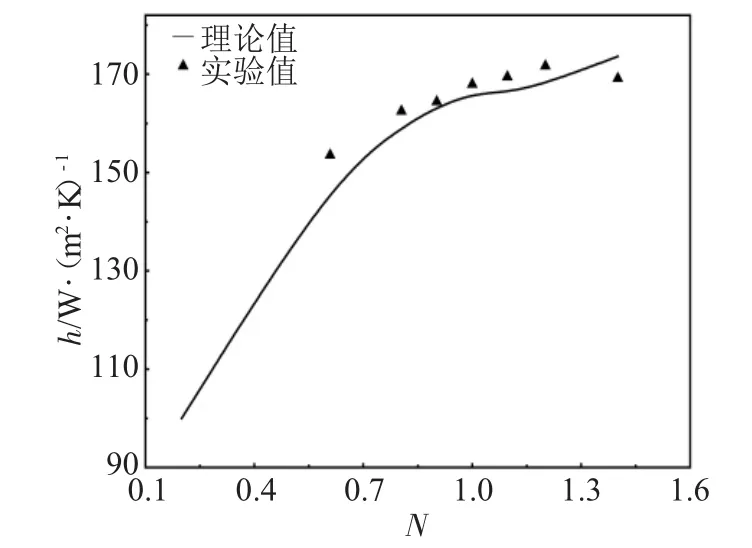
圖6 平均傳熱系數理論計算值與實驗值的比較Fig.6 Comparison of experimental values of the average heat transfer coefficient with calculated values（f=11.2 Hz,H0=130 mm）

從圖6可以看出，理論預測值低于實驗值，可能是在理論模型中單純考慮了床高增加將削弱傳熱，也就是床高加高，振動能量衰減得越快，振動的強化作用越不明顯，床高增加顆粒流化質量變差的緣故，但在實際實驗中，氣體的分布，特別是氣體通過水平管時的流動狀態對傳熱具有較大的影響，如果在管壁附近位置流化質量好于其它位置，則可能使實驗獲得的傳熱系數高于理論預測值。

3.3 管徑對平均傳熱系數的影響

圖7比較了水平管直徑為32mm、床高為95mm、振動頻率為11.2Hz的條件下平均傳熱系數理論預測值與實驗測定值之間的差異。

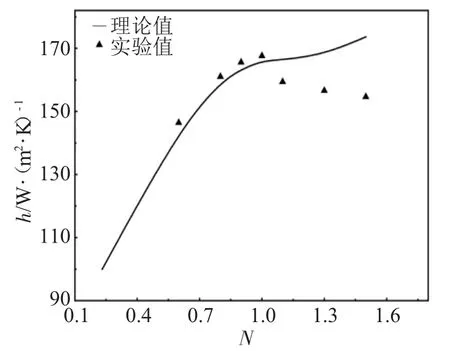
圖7 平均傳熱系數理論計算值與實驗值的比較Fig.7 Comparison of experimental values of the average heat transfer coefficient with calculated values（f=11.2Hz,Dt=32mm,H0=95 mm）

從圖7可以看出，在流化數小于1.0時理論預測值小于實驗值，流化數大于1.0時理論預測值大于實驗值。這可能是由于流化數小時，管背風面未流化的顆粒更多，傳熱減慢；高流化數條件下這層顆粒厚度減薄，而在理論模型中考慮的是管徑對迎風面氣膜和背風面顆粒層的平均影響，所以理論預測與實驗值會有一定的差異。

3.4 理論預測與實驗值的比較

圖8示出了不同條件下部分實驗數據與理論預測值間的比較，所取數據點個數為80。

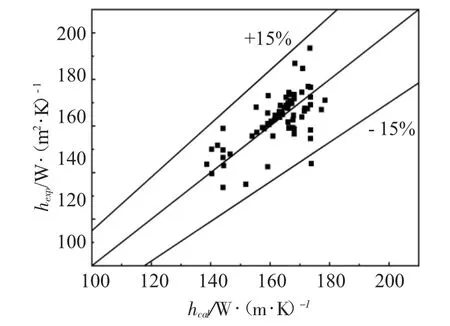
圖8 平均傳熱系數理論預測值與實驗值的比較Fig.8 Comparison of experimental values of the average heat transfer coefficient with calculated values

從圖8可以看出，兩者吻合較好，實驗值與理論預測值間的誤差在±15%以內，表明本研究提出的計算顆粒床層與水平管間的平均傳熱系數數學模型是可靠的。

4 結論

（1）在各種振動頻率下流化數較小時理論預測值和實驗值吻合較好；在較高流化數、低振動頻率時，實驗值處于理論值上方；隨著振動頻率增大，平均傳熱系數實驗值逐漸趨于理論預測值甚至低于理論預測值。

（2）水平管管徑增加，在流化數小于1.0時理論預測值小于實驗值，流化數大于1.0時理論預測值大于實驗值。

（3）通過對振動流化床與浸沒水平管間傳熱特性分析，在顆粒團模型的基礎上，建立了平均傳熱數學模型，并與實驗測定的值進行了比較，實驗結果與模型預測較為一致，表明本研究建立的傳熱模型能正確揭示振動流化床與浸沒水平管間的傳熱規律，對傳熱系數能進行很好的預測。

［1］葉世超.振動流化床水平換熱管傳熱特性研究［D］.四川大學,2000.

［2］N.S.Grewal.Heat transfer between immersed horizontal tubes and bubblingfluidized beds［J］.Trends in Chemical Engineering,1994,2（1）:33-58.

［3］S.W.Jim,J.Y.Ahn,S.D.Kim.Heat transfer and bubble characteristics in a fluidized bed with immersed horizontal tube bundle［J］.International of Heat and Mass Transfer,2003,46（4）:399-409.

［4］S.Rasouli,M.R.Golriz,A.A.Hamidi.Effect ofannular fins on heat transfer of a horizontal immersed tube in bubbling fluidized beds［J］.Power Technology,2005,154（5）:9-13.

［5］ZHU Xuejun,YE Shichao,PAN Xiaoheng.The local heat transfer mathematical model between vibrated fluidized beds and horizontal tubes［J］.Experimental Thermal and Fluid Science，2008,32（6）:1279-1286.