淺析孤立子理論中的達布變換
梁銀雙
(中州大學信息工程學院,鄭州450044)
1.引言
人們在對非線性科學的研究中提出了孤子的概念。早在1834年,英國科學家Scott.Russel就發現了孤子水波,隨著近代數學與物理的發展,人們在流體、等離子體、非線性光學、生物神經傳播等一系列領域中,都觀察到孤立子。孤立子理論已成為非線性科學的一個重要研究領域,它引起人們極大的興趣。另一方面,這一理論又為非線性偏微分方程提供了求顯式解的方法。如反散射方法[1],變換方法[2],Darboux變換方法[3],Hirota雙線性方法[4],齊次平衡法[5],分離變量法[6],對稱約束法[7],Lie 對稱法[8]等。其中,Darboux變換方法是一種自然而美妙的方法。它從平凡解出發,可以得到孤子方程的精確解。這些方法的發現和應用,使得大量的非線性偏微分方程得以成功求解。
2.Darboux變換的起源
1882 年,G.Darboux研究了一個二階線性常微分方程(現在稱之為一維Schr?dinger方程)的特征值問題:

其中,u(x)是給定的函數,稱為勢函數,λ是常數,稱為譜參數。Darboux發現了下面的事實:
設 u(x)和 φ(x,λ)是滿足(2.1)式的兩個函數,對任意給定的常數 λ0,令 f(x)= φ(x,λ0),
即f(x)是(2.1)式當λ=λ0時的一個解。


這樣,借助于f(x)=φ(x,λ0)所做的變換(2.2)將滿足(2.1)的一組函數(u,φ)變化為滿足同一方程的另一組函數(u′,φ′)。這就是最原始的Darboux變換:
(u,φ)→(u′,φ′),在 f(x)≠0 處它是有效的。
3.Darboux變換的基本思路
Darboux變換的基本思路:利用非線性方程的一個解及其Lax對的解,借助于譜問題之間的規范變換,得
則這里所定義的函數 u′(x)和 φ′(x,λ)也滿足(2.1)式,即到Darboux變換,然后通過代數運算及微分運算來得出非線性方程的新解和Lax對相應的解。
近年來,Darboux變換方法得到迅速發展,已成功地應用于求解一系列與特征值問題相聯系的非線性孤子方程的顯式解,發展趨勢由一維到多維,由單一的孤子演化方程到耦合演化方程組。[9]Darboux變換的優點非常明顯,只需作一次完全可積的線性方程組的求解,然后就可用代數運算來得到非線性孤子方程的新解。
4.KdV方程的Darboux變換
下面以KdV方程為例來說明方法。

關于φ的線性方程組

這里 u,φ 均為 x,t的函數。
命題 KdV方程(4.1)是方程組(4.2)的可積條件。
證明 由(4.2)的第一式得出φxx=(-λ-u)φ

由方程組(4.2)的第二式得
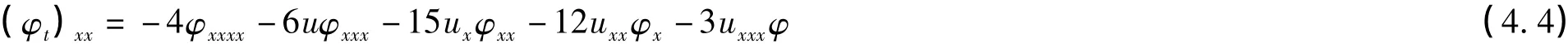
方程組(4.2)可積的充要條件是(4.3)與(4.4)相等,且對任意λ成立,則u需滿足KdV方程(4.1)式。因此KdV方程(4.1)是方程組(4.2)的可積條件。同時方程組(4.2)也稱為KdV方程的Lax對。
進一步驗證還發現上述Darboux變換(2.2)也適用于KdV方程(4.1)。
即有如下定理:
定理 如果已知KdV方程的一個解u,通過解線性方程組(4.2)得到φ(x,t,λ),取λ得一個值λ0,得到
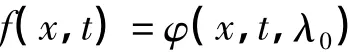
由Darboux變換(2.2)就可獲得KdV方程的一個新解u′,同時(2.2)中的φ′為相應的Lax對的解。
證明 設從KdV方程的平凡解u=0出發,此時線性方程組(4.2)可化為:

根據λ的取值分兩種情況來討論方程組(4.5)的解。
取 λ0=-1,則 f(x,t)= φ(x,t,-1)=ex+4t,lnf(x,t)=x+4t
代入 Darboux變換(2.2)得 u′=0。
其中,c1,c2為任意常數。
取 λ0=1,則 f(x,t)= φ(x,t,1)=cos(x+4t),lnf(x,t)=ln cos(x+4t)
代入Darboux變換(2.2):
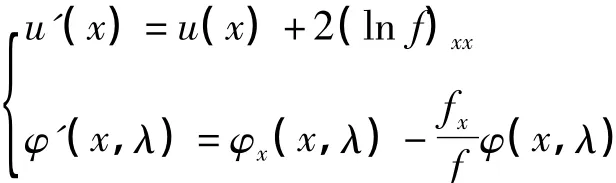
得:
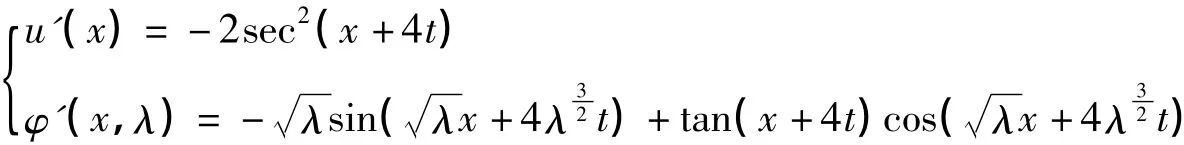
其中u′(x)為KdV方程的一個新解,同時φ′(x,λ)為相應的Lax對的解。
[1]Ablowitz M J,Clarkson P A.Solitons&nonlinear evolution equations and Inverse Scattering[M].Cambridge University Press,1991.
[2]Rogers C,Schief W K.Darboux Transformations,Geometry and Mordem Applications in Soliton Theory[M].Cambridge University Press,2002.
[3]Matveev V B,Salle A M.Darboux Transformation and Solitons[M].Springer,Berlin,1991.
[4]Hirota R.The Direct Method in Soliton Theory[M].Cambridge University Press,2004.
[5]范恩貴.齊次平衡法,Weiss-Tabor-Carnevale及Clarkson-Kruskal約化之間的聯系[J].物理學報,2000(49):1409.
[6]Lou S Y,Chen L L.Formal variable separation aproach for nonintegrable models[J].J.Math.Phys,1999(40):6491.
[7]Lou S Y,Hu X B.Infinitely many Lax pairs and Symmetry constraints of the KP equation[J].J.math.phys,1997(38):6401.
[8]Tu G Z.A new Hierarchy of Integrable Systems and Its Hamiltonian Structures[J].Scientia.Sinica,1988,31(12):28.
[9]谷超豪,胡和生,周子翔.孤立子中的Darboux變換及其幾何應用[M].上海:上海科技出版社,1999.

