基于Metropolis-Hastings算法的α穩定分布參數估計

馬洪斌，馬巖，楊春梅，沈鋒

(1.哈爾濱理工大學 機械動力工程學院，黑龍江 哈爾濱150080;2.東北林業大學 機電工程學院，黑龍江 哈爾濱150040;3.東北林業大學 研究生院，黑龍江 哈爾濱150040;4.哈爾濱工程大學 自動化學院，黑龍江 哈爾濱150001)

0 引言

在傳統的信號處理中，由于高斯模型可以很好地描述許多信號噪聲并且算法結構簡單，通常假定接收機接收的信號噪聲為高斯分布白噪聲[1]，然而，在實際的情況中所遇到的許多信號或噪聲往往具有顯著地尖峰脈沖特性，例如水聲信號、低頻大氣噪聲、生物醫學信號和金融數據等[2－4]。這類信號的統計特性明顯區別于高斯信號的分布特點，表現在其概率密度函數具有比高斯分布更厚的拖尾，而且概率密度函數往往是非對稱的。在這種背景下，基于高斯假定設計的信號處理系統會出現性能退化。而α穩定分布為這類信號提供了良好的數學模型從而得到廣泛的研究和應用[5－9]，α穩定分布是目前惟一的一類滿足廣義中心極限定理的分布，由于可以描述更加廣泛的數據，因此具有更普遍的意義。

α穩定分布參數估計的方法主要有最大似然法、樣本分位數法、樣本特征函數法和負階距法等[1，10－11]。最大似然估計法屬于復雜的非線性優化問題，沒有初始值選擇原則和收斂分析可供使用，并且計算量相當可觀;樣本分位數的方法受到查找表的制約，只能進行模糊估計;特征函數法、負階距法都可以準確的估計α穩定分布的參數而且計算方便，但是僅適用于對稱α穩定分布，無法對偏斜參數β進行估計，實際應用中存在很大的局限性。貝葉斯估計克服了以上缺點，應用MCMC動態模擬的方法在已知待估計參數先驗分布的條件下可以準確地估計出α穩定分布的所有4個參數。

1 α穩定分布模型

由于α穩定分布不存在封閉的概率密度函數，所以通常用特征函數來描述。一維的α穩定分布特征函數為

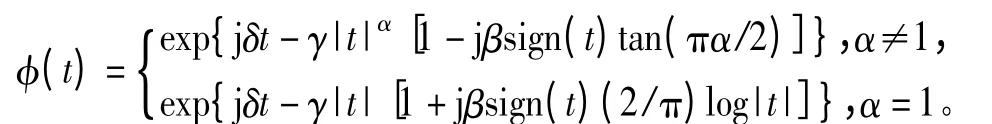
式中:sign(·)為符號函數;參數 α∈(0，2]稱為特征指數，他決定該分布脈沖特性的程度。α值越小，所對應分布的拖尾越厚，因此脈沖特性越顯著，當α=2時，此分布成為均值為μ方差為2γ的高斯分布。當α=1且β=0時為柯西分布;參數β∈(－1，1)稱為偏斜參數，用于確定分布的斜度，β＞0分布右偏，β＜0分布左偏，β=0分布對稱，簡稱為SαS，高斯分布和柯西分布都屬于SαS分布;參數γ為分散系數，又稱尺度系數，他是關于樣本相對于均值的分散程度的度量，由于α穩定分布不存在有限的方差，所以使用分散系數來描述分布的偏離均值的程度;參數δ稱為位置參數，對于SαS，在α∈(1，2]時δ表示分布的均值，在α∈(0，1]時表示分布的中值。若隨機變量x服從于 α 穩定分布，則記為 x～Sα(γ，β，δ)。

2 α穩定分布的貝葉斯模型

貝葉斯推斷的本質就是利用觀測數據把參數的先驗概率分布轉化為相應的后驗概率分布。若用X表示觀測值，用θ表示未知參數，則未知參數θ的后驗概率密度p(θ|X)可根據貝葉斯條件概率準則推出，即

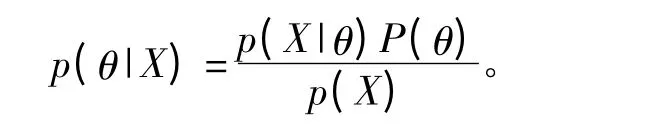
其中:p(θ)是未知量的先驗概率密度;p(X|θ)是參數 θ 的似然函數;全概率 p(X)=∫p(X|θ)P(θ)dθ被稱為歸一化常數，貝葉斯定理可簡化表示為p(θ|X)∝p(X|θ)P(θ)，式中∝ 表示兩邊僅相差不依賴θ的常數因子。因此，把貝葉斯推斷中所有的未知參數視為隨機變量，利用觀測數據的似然函數和未知參數的先驗信息通過計算未知參數后驗概率密度函數，得到未知參數的估計值。

在利用貝葉斯推斷估計α穩定分布的參數時，首先建立α穩定分布的貝葉斯推斷模型，未知參數可確定為 θ=(α，β，γ，δ)。假定 α 穩定分布的四個參數相互獨立，那么利用貝葉斯層次模型表示為

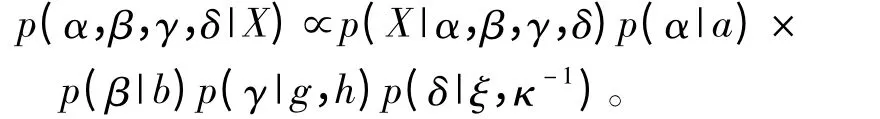
式中，a、b、g、h、ξ、κ 是先驗分布的超參數。根據未知參數的分布特點假設參數α，β的先驗分布是在定義域內的均勻分布，a，b各為參數 α，β定義域區間長度，參數γ服從以(g，h)為超參數的逆伽馬分布，參數δ服從以(ξ，κ－1)為超參數的正態分布，各先驗分布為

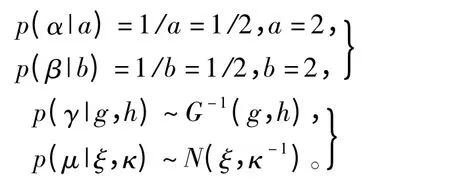
3 基于M－H算法的MCMC模擬

運用貝葉斯方法估計參數時，由于在求解歸一化因子的過程中存在多維積分問題，未知參數的后驗分布無法求得解析解，因此無法單純運用在參數估計的過程中，但是應用 MCMC(Markov chain Monte Carlo)[13]的方法解決貝葉斯估計中的多維數值積分問題，MCMC方法是以動態構造Markov鏈為基礎，通過遍歷性約束來實現模擬目標分布的一類隨機模擬的方法。當應用在貝葉斯估計時，以未知參數的后驗分布為目標函數，采用Gibbs采樣法或者Metropolis Hastings采樣法，通過隨機模擬產生收斂到目標函數Markov鏈，從而得到未知參數的估計值。在實際計算中，采用間隔k個點采樣一次，這樣可以減小相鄰采樣點的相關性，得到的樣本可以近似看做是獨立同分布的樣本。

采用M－H采樣法對α穩定分布進行參數估計，令 θ=(α，β，γ，δ)構造以當前狀態 θ(t)為均值，標準差為σ的正態分布為建議分布即q(·|·)～N(θ(t)，σ)，新候選點 θ*應表示為

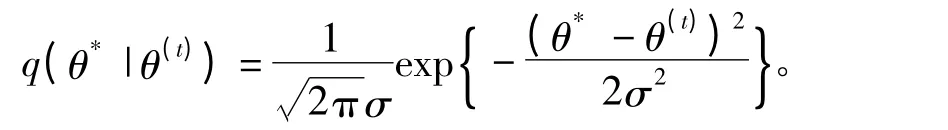
根據α穩定分布的貝葉斯推理模型和M－H算法，可以推導出α穩定分布參數估計的更新過程以及相應的接受概率，以特征指數α為例，具體步驟如下:

1)對于特征指數α，假設Markov鏈當前狀態為(t，α(t))，從提議函數 q(·)抽取候選點 α*，即 α*～ q(α*|α(t))。

2)計算接受概率Aα

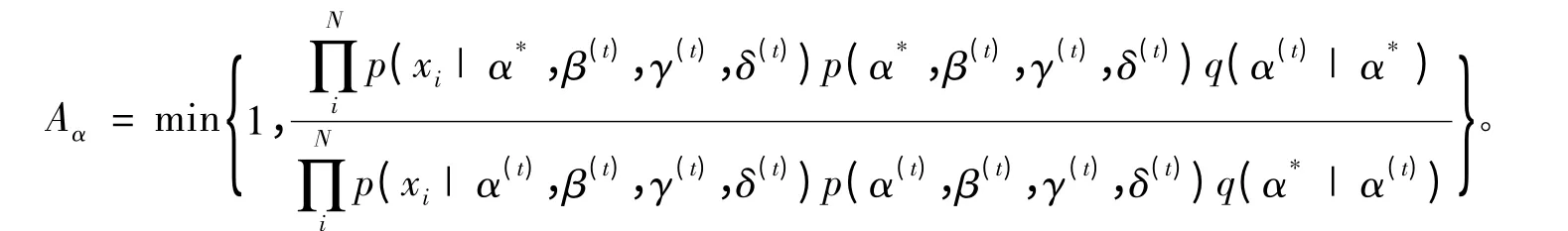
由于(α，β，γ，δ)4 個參數分別獨立，則 Aα為

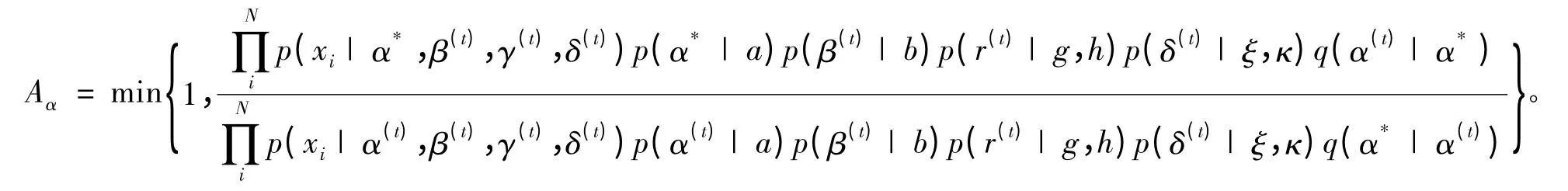
考慮到提議函數為對稱分布，且p(α)為均勻先驗，那么接受概率可簡化為:

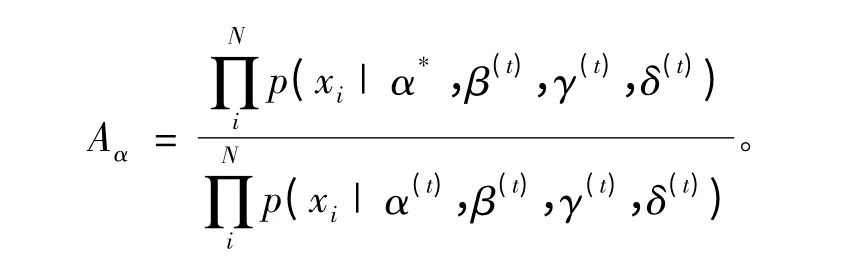
3)生成隨機數 u～U(0，1)，如果 u≤Aα則接受候選點α*，Markov鏈狀態值進行更新，否則拒絕候選點，Markov鏈狀態保持不變，然后循環步驟1)，直到目標分布趨于平穩。

對偏斜參數、分散系數和位置參數使用與特征指數相同的策略，令 β*～ q(β*|β(t))，γ*～ q(γ*|γ(t))，δ*～ q(δ*|δ(t))，計算可得接受概率 Aβ，Aγ，Aδ分別為

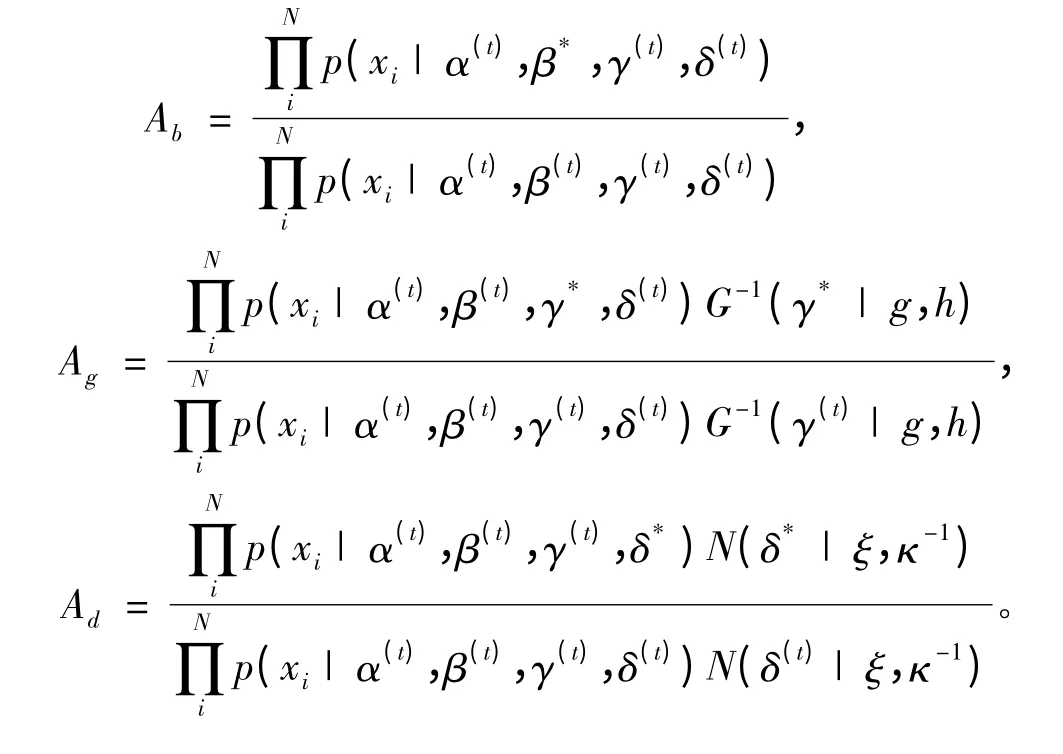
4 仿真結果與分析

4.1 特征指數{α}估計

假設穩定分布參數{β，γ，δ}已知，僅特征指數α未知，當α取不同值時，利用提出的方法對其進行估計。仿真條件設置:在標準穩定分布下(β=0，γ =1，δ=0)，取樣本數 N=1 000，迭代次數 10 000，burn－in時間1 000 s，超參數 g=1，h=1，κ =1。當α≤1時 ξ=median(y)，當 α ＞1時 ξ=mean(y)，提議分布的標準偏差σα=0.15。在仿真過程中應用Chambers－Mallows－Stuck的方法產生待估計參數的α穩定分布隨機變量，在穩定分布參數為(α=0.6，β=0，γ =1，δ=0)情況下，產生的1 000 個隨機樣本點如圖1、圖2所示，可見α穩定分布相比高斯分布具有更強的脈沖特性，在β=0對稱的條件下，圖2表現出在中心位置的兩側隨機樣本的數量大致相同。

圖3、圖4給出了當α取不同值時，特征指數α的估計效果以及Markov鏈的自相關時間曲線。可見本文提出的參數估計方法對任意特征指數α都有很好的估計效果，Markov鏈混合性能良好。在提議函數方差不變的情況下，隨α值的增大，估值的標準偏差略有增大，而自相關函數值減小，Markov鏈可以穩定收斂。表1給出了當α取不同值時，初始值α0、估計值、標準偏差 Std.Dev、M －H 接受概率以及自相關時間的統計數據。統計結果表明算法適用于任意α∈(0，2]值的估計，且具有較高的估計精確度。

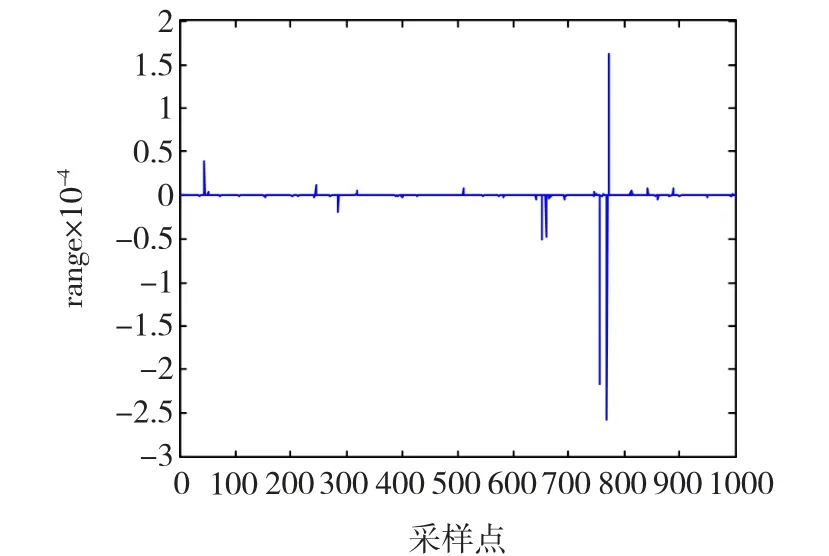
圖1 α穩定分布下1 000個隨機樣本點Fig.1 1000 random variables for α-stable

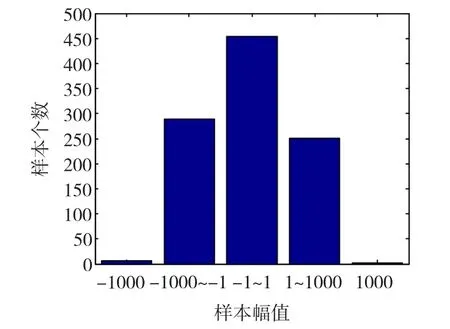
圖2 隨機樣本點分布圖Fig.2 Distribution of random variables

圖3 特征指數α的估計效果Fig.3 α estimation results

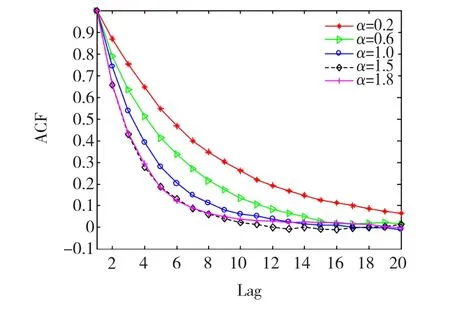
圖4 Markov鏈自相關時間Fig.4 Correlation time of Markov

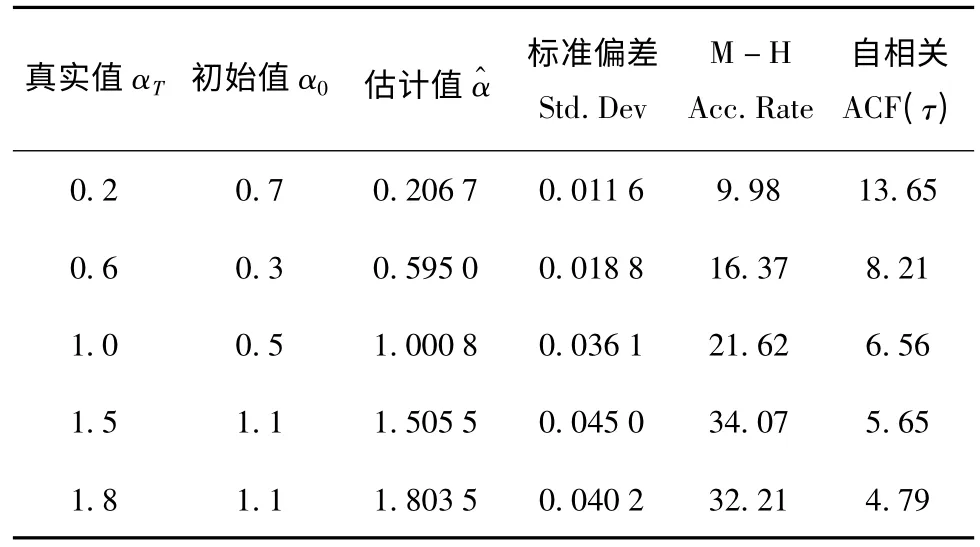
表1 特征指數α的估計效果Table 1 α estimation results

4.2 參數{α，β，γ，δ}聯合估計

前面的仿真實驗中，均假定參數{β，γ，δ}已知，但一般情況下這種假設是不成立的。在實際應用中，觀測值往往反映出分布的某種偏斜特性;當α值較小時，樣本均值與真實位置參數也相去甚遠，而分散系數也有別于高斯分布的方差，這些都會影響分布模型的準確性，因此必須對其進行可靠的估計。

為了驗證提出的方法的正確性，仿真實驗按照偏斜參數的不同分兩種情況:1)β＜0;2)β＞0。仿真條件設置:樣本數N=1 000，迭代次數為10 000，burn－in時間 1 000;超參數 g=1，h=1，κ =1，當α≤1時 ξ=median(y)，當 α ＞1時 ξ=mean(y)，提議函數的標準偏差 σ ={0.15，0.1，0.1，0.2}。

圖5和圖6給出了兩組仿真實驗的參數估計效果。從中可以發現，在不同的仿真條件下，Markov鏈都有良好的混合性能，表現為在支撐域附近強烈的擺動，每條鏈均可靠的收斂到目標分布，準確地估計出了特征指數α、偏斜參數β、分散系數δ和位置參數δ。兩組仿真實驗綜合 α＜1和α＞1，以及β＜0、β＞0典型情況，因此測試結果表明該方法對具有不同偏斜特性的任意α穩定分布參數的組合都適用，且估計性能不受參數取值范圍的限制。另外，從圖中可以看出，由于參數之間的相互影響以及不同的α穩定分布參數組合結構，使得在給定的提議函數和不變方差條件下，估計值會有不同的標準偏差。表2給出了上述3種情況下，α 穩定分布參數的真實值 θT、初始值 θ0、估計值、標準偏差、M－H接受概率和自相關時間的統計數據。統計結果也表明，提出的方法不僅實現了任意特征指數α的準確估計，而且他能夠以同樣的精度估計出偏斜參數β、分散系數γ以及位置參數δ，這一點在實際應用中是非常重要的，但傳統的方法往往無法實現。

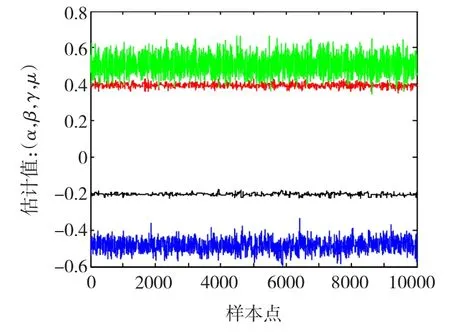
圖5 參數聯合估計效果(β＜0)Fig.5 Joint parameters estimation result(β ＜0)

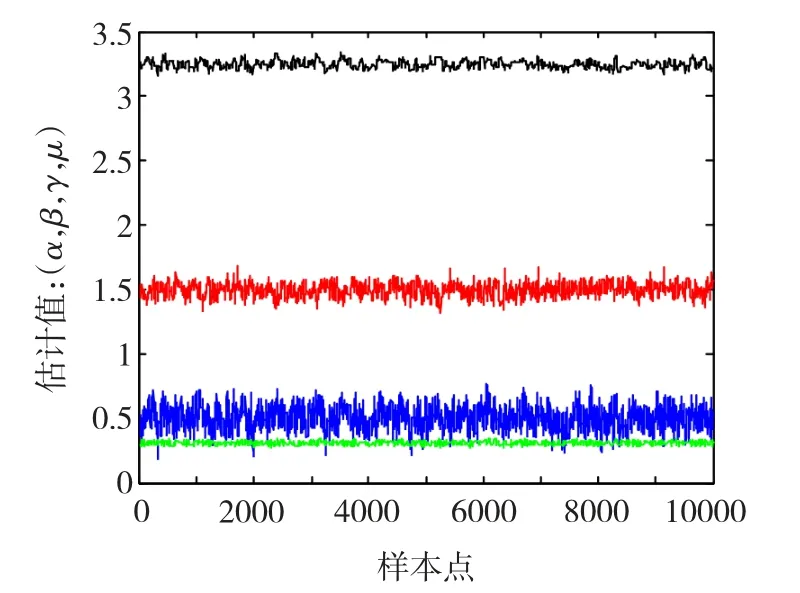
圖6 參數聯合估計效果(β＞0)Fig.6 Joint parameters estimation result(β ＞0)

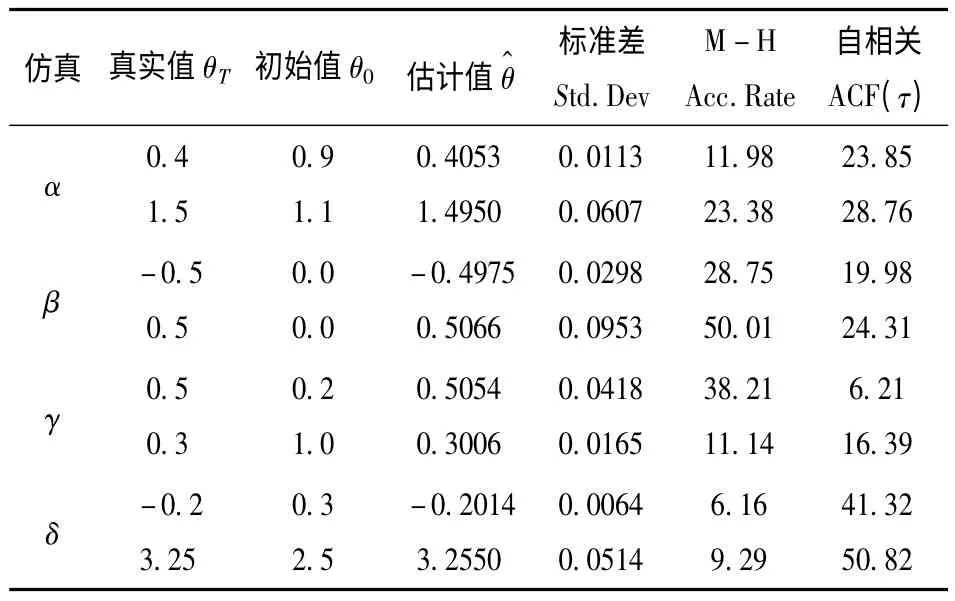
表2 參數估計效果Table 2 Parameters estimation result

5 結語

α穩定分布可以很好地描述具有顯著尖峰脈沖波形和重尾的非高斯現象，是一種非常有效的統計信號處理工具。本文針對非對稱α穩定分布參數估計問題，在貝葉斯統計推理的框架下，提出一種基于MCMC動態模擬的參數估計新方法。該方法實現了對任意α穩定分布參數的估計，參數估計精度高且不受取值范圍的限制，特別是它克服了傳統方法無法估計偏斜穩定分布的不足。同時需要指出的是，本文的估計結果是在Markov鏈可靠收斂，提議函數合理有效的前提下給出的，如何設計更好的提議函數，增加算法效率以及開發利用α穩定分布解決實際問題將是下一步的研究重點。

[1]HAO M，NIKIAS C L.Signal processing with fractional lower order moments:stable processes and their applications[J].Proceedings of the IEEE，1993，81(7):986－1010.

[2]ROENKO A A，LUKIN V V，DJUROVIC I.Two approaches to adaptation of sample myriad to characteristics of SαSdistribution data[J].Signal Processing，2010，90:2113 －2123.

[3]SALAS Gonzalez D，KURUOGLU E E，RUIZ D P.Modelling with mixture of symmetric distributions using Gibbs sampling[J].Signal Processing，2010，90:774－783.

[4]司偉建，蔣鵬，劉旭波.改進的三次相位函數法LFM雷達信號參數估計[J].哈爾濱工程大學學報，2012，33(6):771－774.SI Jianwei，JIANG Peng，LIU Xubo.The parameter estimation of an LFM radar signal based on a modified cubic phase function[J].Journal of Harbin Engineering University，2012，33(6):771－774.

[5]ARIKAN O，BELGE M，CETIN A E，et al.Adaptive filtering approaches for non-gaussian stable process[C]//International Conference on Acoustics，Speech，and Signal Processing，ICASSP －95，1995，2:1400－1403.

[6]TSIHRINTZIS G A，NIKIAS C L.Evaluation of fractional lowerorder statistical-based detection algorithm on real sea-clutter data[J].IEE Proceedings on radar，sonar navigation，1997，144(1):29－38.

[7]MA X，NIKIAS C L.Joint estimation of time delay and frequency delay in impulsive noise using fractional lower order statistics[J].IEEE Trans on Signal Processing，1996，44(11):2669－2687.

[8]朱曉波，王首勇，李旭濤，等 非高斯雜波中的MIMO雷達信號分離[J].系統工程與電子技術，2010，32(6):1210－1214.ZHU Xiaobo，WANG Shouyong，LI Xutao，et al.MIMO radar signal separation in non-Gaussian clutter[J].System Engineering and Electronics，2010，32(6):1210 －1214.

[9]唐洪，邱天爽.Alpha穩定分布噪聲環境下廣義恒模算法收斂性能的研究[J].電子學報，2009，37(1):118－121.TANG Hong，QIU Tanshuang.Convergence properties of the GCMA in alpha-stable noise environment[J].Acta Electronics Sinica，2009，37(1):118 －121.

[10]KURROGLU E E.Signal Processing in alpha-stable Noise Environments:A Least lp-Norm Approach[D].University of Cambridge，1998.

[11]LOMBARDI M J.Bayesian inference for α-stable distributions:A random walk MCMC approach[J]，Computational Statistics＆Data Analysis，2007，51:2688－2700.

[12]SALAS Gonzalez D，KURUOGLU E E，RUIZ D P.Finite mixture of α-stable distributions [J]，Digital Signal Processing，2009，19:250－264.

[13]LAINE M.Adaptive MCMC methods with applications in environmental and geophysical models[D].Finnish Meteorological Institute Helsinki，2008.