考慮弧垂的交流特高壓輸電線三維電磁場

蘭生，張振興，原永濱

(福州大學 電氣工程與自動化學院，福建 福州350108)

0 引言

隨著社會經濟的快速發展，用戶對電能的需求越來越大，加之我國能源分布的不平衡，需要加快建設特高壓輸電網[1]。特高壓輸電可能夠實現大容量、遠距離輸電，降低損耗，節省線路走廊，有利于構建堅強電網[2]。我國的特高壓交流輸電額定電壓等級為750 kV和1 000 kV，是目前國內最高電壓等級[3]。目前，中國正在運行的特高壓交流輸電線路示范工程，即晉東南—南陽—荊門1 000 kV特高壓交流輸電，為最新應用。對特高壓輸電線路的電磁環境進行的一些研究，主要包括工頻電場、工頻磁場、無線電干擾和可聽噪聲等理論以及試驗研究，并取得了一系列成果。特高壓輸電線路工頻電磁場對其附近的人和生態是否會帶來危害，一直以來都是大眾十分關心的問題。通過特高壓試驗線路或正在運行的超高壓線路進行電磁測量和生物效應研究，作為主要依據來制定電磁環境限值。線路產生的電磁場已經成為輸電工程中關鍵的影響因素[4]。因此，電磁場的數值計算成為特高壓輸電的一個關鍵技術。工程電磁場數值計算方法，主要包括有限元法以及逐次鏡像法、模擬電荷法、矩量法等[5]。文獻[3]提出了基于有限元法建立模型，計算分析了特高壓緊湊型輸電線路附近場強以及導線表面場強。文獻[6]采用了逐次鏡像法計算特高壓輸電線路各種塔型導線下方電場強度和導線表面場強。文獻[7]利用復鏡像理論計算了特高壓輸電線路工頻磁場，但是求解誤差受到鏡像次數影響，如果導線間的最小距離與導線半徑比值越大，鏡像次數越少，那么誤差會變大。文獻[8]采用了模擬電荷法，通過Matlab仿真實現了超高壓輸電線路周圍電磁場計算，在精確度上存在較大誤差。文獻[9]利用有限元—有界元法，進行電磁場開域求解。有限元法作為一種求解邊界問題方法，已經有很多成熟應用的有限元軟件，能夠靈活選擇網格剖分精確度。目前，利用有限元法計算特高壓輸電線路下方電磁場，大多是把輸電線路等效為直導線模型。本文針對特高壓輸電線路的實際線路的弧垂情況，進行電磁有限元仿真，使計算結果更加接近真實值。

1 電磁場計算理論

由于架空輸電線路產生的工頻電磁場滿足，周圍場點到導線的距離遠小于相應的時諧電場在空氣中的波長，可以近似為準靜態場。故可類比地采用靜態電磁場的分析方法與結論進行相應的分析與計算。因此可以得到電準靜態場所滿足的麥克斯韋方程，即

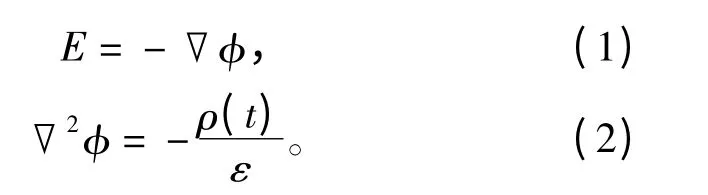
同理，磁準靜態場也滿足

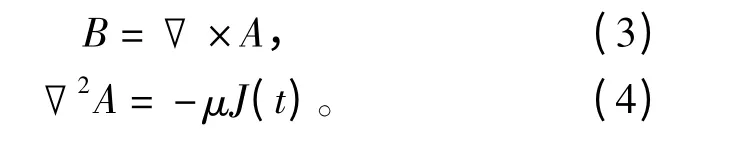
式中，μ和ε分別為介質的磁導率和介電常數，B和A分別表示磁通密度和矢量磁位。?2為拉普拉斯算子，即

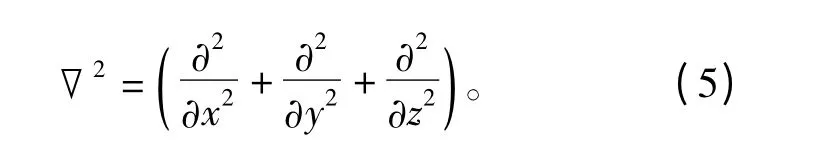
狄利克萊邊界條件表示為

式中:Γ為狄利克萊邊界;g(Γ)是位置的函數，可以是常數或者零。

諾依曼邊界條件可表示為

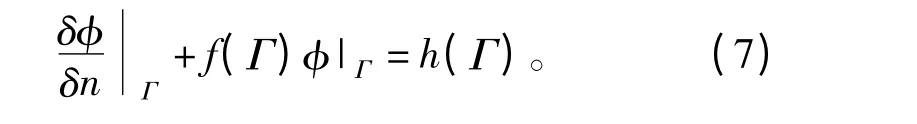
式中:Γ為諾依曼邊界;n為邊界Γ的外法線矢量;f(Γ)和h(Γ)為一般函數(可為常數或零)，當為零時為奇次諾依曼條件。

由于在電磁場微分方程的求解中，只有邊界條件和初始條件限制，方程才能有定解，故需要設置邊值和初值。

在磁場有限元分析中，當場是作正弦變化且頻率較低時，準靜態磁場可用時諧場來求解。本文計算的是實際交流特高壓輸電線路周圍磁場分布，故可采用時諧磁場進行計算。

以磁感應強度為例，b(r，t)可由復數函數的實部表達為

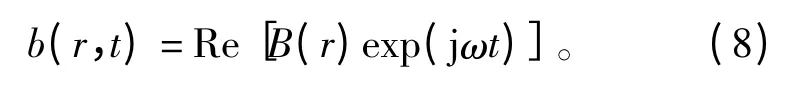
其中:

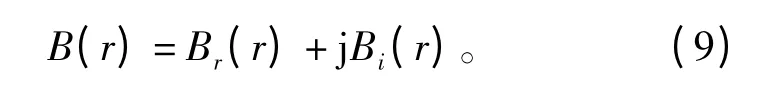
上式中，Re[]為復數實部記號。Br(r)和Bi(r)分別對應B(r)的實部和虛部，B只有空間坐標決定。

2 電磁場仿真

2.1 線路基本數據

交流特高壓輸電線路額定電壓為1 000 kV，最高運行電壓1 100 kV，額定相電流4 000 A。桿塔結構為酒杯型，如圖1所示。單回三相導線水平I－V－I排列，相間距離為22.2 m;桿塔頂端兩側裝設避雷線，兩根架空地線相距46 m，距導線垂直距離22.33 m。三相子導線選擇鋼心鋁絞線，型號為ACSR－720/50，每相采用對稱八分裂導線，分裂間距為40 cm。架空地線選擇光纖復合鋁包鋼絞線(OPGW)，導線規格為500 mm2，導線分裂根數為2根。在計及懸鏈線時，取檔距 L=400 m，由文獻[10]弧垂計算公式，可得弧垂高度s=10.24 m。

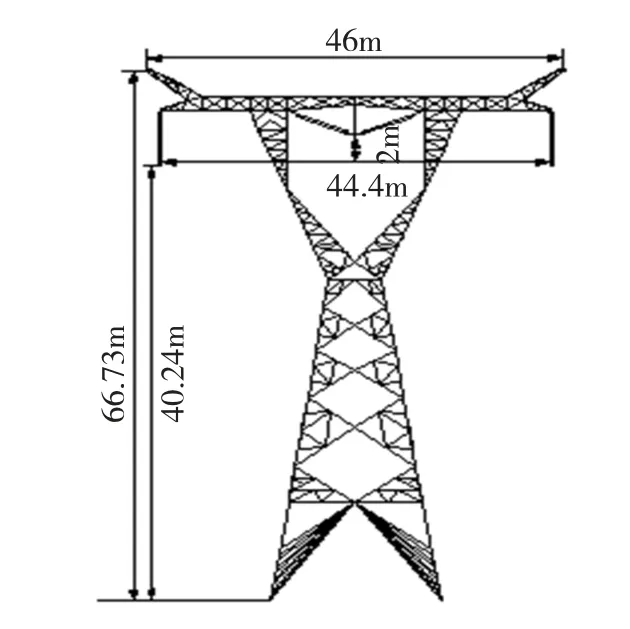
圖1 酒杯塔Fig.1 Glass tower

2.2 三維電磁場建模

由于實際特高壓輸電線路比較復雜，而且有些因素的影響可以忽略不計，因此有必要對實際線路進行合理地簡化。本文對輸電線路三維模型作如下簡化[11]:

1)地面是無窮大導體，電位為零，沿線地面電阻率相同;

2)輸電導線分別用長直導線和懸鏈線代替而且同一檔距內的同型導線具有相同等效半徑且彼此平行，導線表面等電位，導線為等磁位面;

3)只考慮線路主要部分形成的電磁場，忽略桿塔、金具、絕緣子等附近物體的影響，不考慮導線、架空地線的端部效應;

4)認為電荷分布沿線路分布沒有畸變，不考慮線路上電位的變化;

5)假設線路電流為正弦穩態電流，并沿導線軸線流動。

通過簡化，分裂導線建模時采用文獻[12]中的等效半徑計算式(10)，求出相導線的等效半徑。

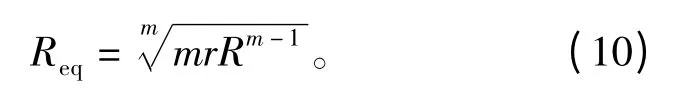
式中:m為分裂根數;r為子導線半徑，單位m;R為分裂導線外接圓半徑，單位m。

模型建立時，以檔距中央為坐標原點。電場建模時，對于長直導線模型，導線對地高度取最大弧垂處的高度。邊界和地面圍成的半徑120 m，長度400 m的上半圓柱體為空氣域，其底面圓心坐標為(－200，0，0)，與地面、導線組成求解區域。對于磁場，需加上大地區域，大小與空氣區域一樣。特高壓輸電線路計算三維模型如圖2所示。

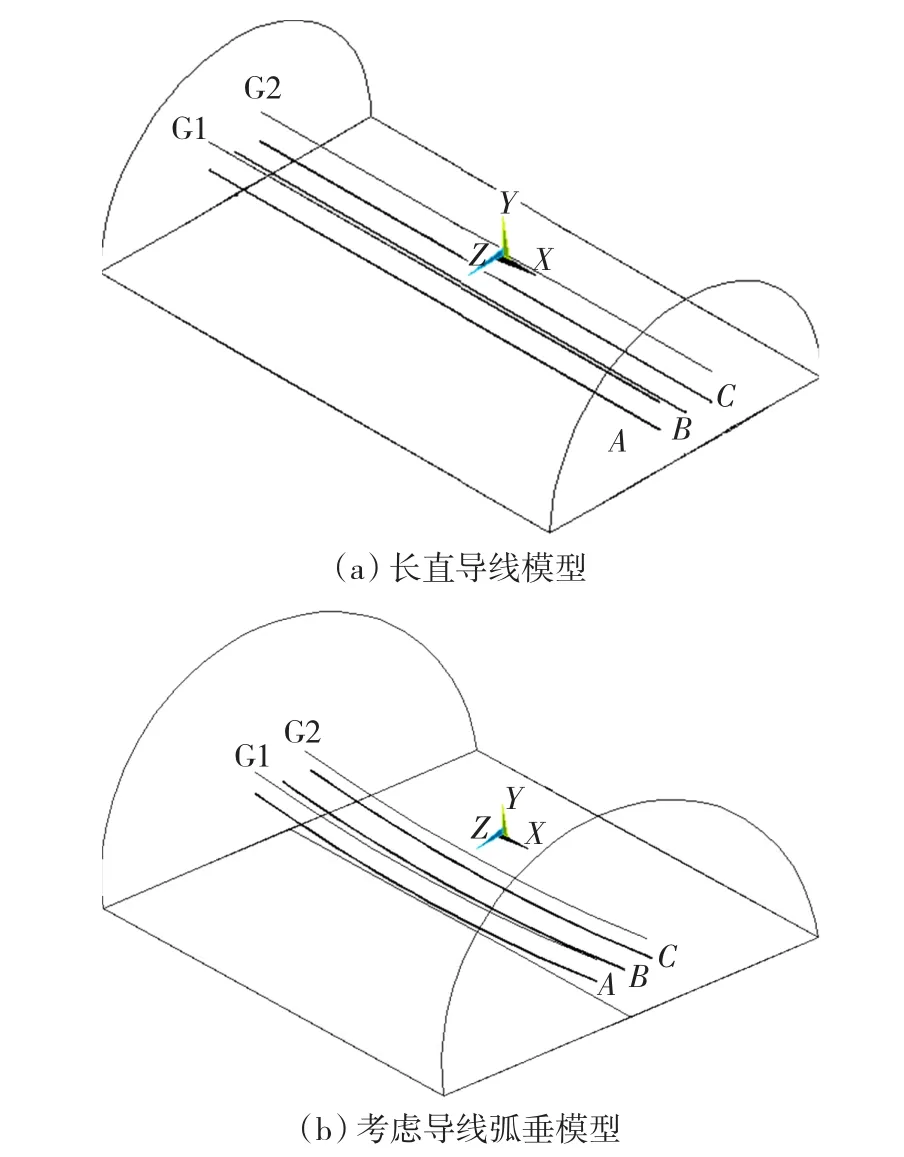
圖2 三維模型Fig.2 3D model

2.3 模型求解

電場計算時，邊界電位取為零。電壓采用額定運行電壓的105%，即1 050 kV。由于每一時刻下得到的電場強度是瞬時值，又導線表面電場線方向垂直于導線表面。因此，電場求解時候，可按A相初始相角為0°和90°分別施加電壓載荷，取求解點2次計算結果的均方根，得到該點電場強度的有效值[13]。地面上電場水平分量近似為0，可認為近似垂直地面，那么這種計算方法可用于地面電場求解。

對于準靜態磁場求解，采用的是諧波場的分析方法。需對磁場的外邊界施加磁力線平行條件。電流載荷分成實部和虛部加載，分別得到磁場的實部和虛部求解值，再將兩者合成，得到磁場的有效值。

3 工頻電場仿真結果與分析

3.1 長直導線模型三維電場仿真結果

采用簡化的長直導線計算模型，通過ANSYS仿真后，將地面上方1.5 m檔距中央(x=0)投影處的兩次電場強度導出。利用Excel，以離線路中心距離為x軸，電場強度為y軸，得到導線下方地面上工頻電場橫向分布，如圖3所示:

由圖3，可總結出線路下方地面上工頻電場橫向分布規律:電場關于線路中心對稱，電場最大值出現在兩邊相外側附近，線路中心投影點兩側分別沿軸線正反方向衰減，衰減到邊相附近開始增大直至最大值，隨著距邊相投影點距離增大，電場強度衰減很快。

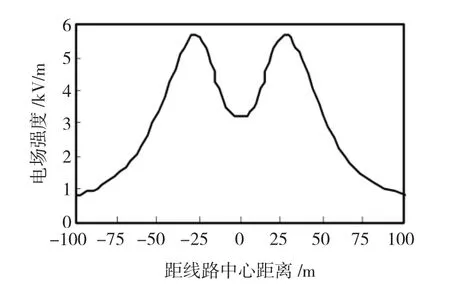
圖3 長直導線工頻電場橫向分布(y=1.5)Fig.3 Rectilinear conductor model(y=1.5)

3.2 考慮導線弧垂三維電場仿真結果

同理，利用 ANSYS仿真后，分別選取 x=0 m、x=100 m、x=200 m 3個截面，得到其工頻電場橫向分布，如圖4所示。

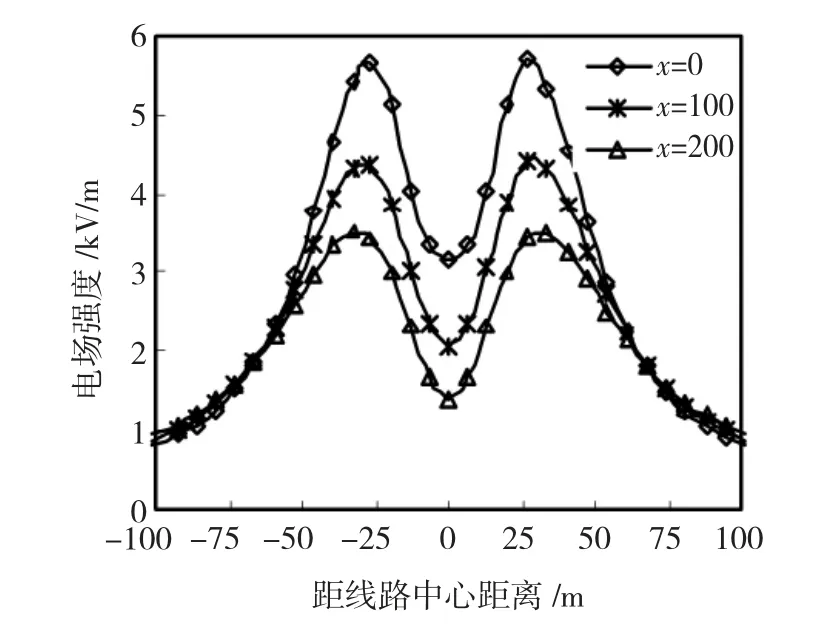
圖4 考慮導線弧垂工頻電場橫向分布(y=1.5)Fig.4 Considering sag model(y=1.5)

圖4 可反映出電場分布的橫向和縱向特征，仿真所得電場分布呈軸對稱形:沿橫向，電場分布出現兩個峰值，位于邊相外側投影附近;沿縱向，朝導線軸向衰減，電場強度最大值出現在輸電線路的弧垂最大處，桿塔處場強最小。

3.3 兩種三維模型的仿真結果比較分析

將圖3與圖4比較，可以得出以下幾點:

1)長直導線模型能反映出輸電線路電場的橫向分布特征。

2)三維模型能夠同時反映輸電線路下方電場的橫向與縱向分布特征。沿縱向，朝兩側方向衰減，電場強度最大值出現在輸電線路的弧垂最大處，桿塔處場強最小。

3)兩種模型在弧垂處數值一樣。離檔距中心越遠，兩種計算模型所得的電場值差別越大。

說明考慮導線弧垂的三維模型更為準確，能夠更為細致地反映線下電場的分布規律。

3.4 仿真結果與實測值對比分析

文獻[14]在特高壓交流試驗示范工程試運行期間，所測得的農田區域導線最大弧垂處電場橫向分布如圖5所示。與本文最大弧垂處下方電場強度的計算結果對比，兩者的橫向分布特征一致，數值略微偏小。本文計算得到的特高壓線路下方場強最大值接近6 kV/m，根據現有我國特高壓輸電線路工頻電場制定的限值，仍然符合要求。

圖5 特高壓輸電線路下方工頻電場橫向分布Fig.5 Transverse distribution of the electric field under UHV AC transmission line

4 工頻磁場的計算結果

4.1 長直導線模型三維磁場的計算結果

采用簡化的長直導線計算模型，通過計算后，得到線路下方工頻磁場實部分量、虛部分量、合成分量的橫向分布，如圖6所示。

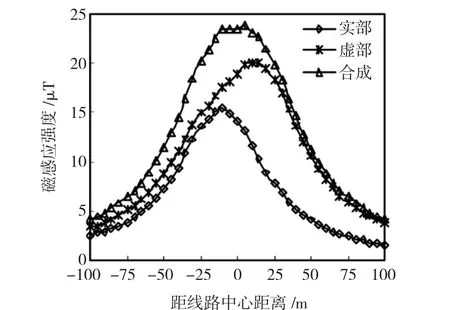
圖6 長直導線工頻磁場橫向分布(y=1.5)Fig.6 Rectilinear conductor model(y=1.5)

從圖6可以看出，磁感應強度的實部、虛部分布呈不對稱分布，這是由于三相導線電流的實部或虛部不可能一樣，因此產生的磁場疊加后也不對稱。合成磁感應強度關于線路中心對稱，其最大值符合我國特高壓輸電線路工頻磁場限值要求。工頻磁場分布規律:磁感應強度最大值出現在線路中心，在三相導線投影范圍內，磁感應強度變化很小，在邊相導線投影外側，磁感應強度明顯降低。

4.2 考慮導線弧垂三維磁場仿真結果

通過計算后，為了分析考慮導線弧垂模型時，地面上方工頻磁場的變化情況，分別選取x=0 m、x=100 m、x=200 m 3個截面，得到其工頻磁場橫向分布，如圖7所示。

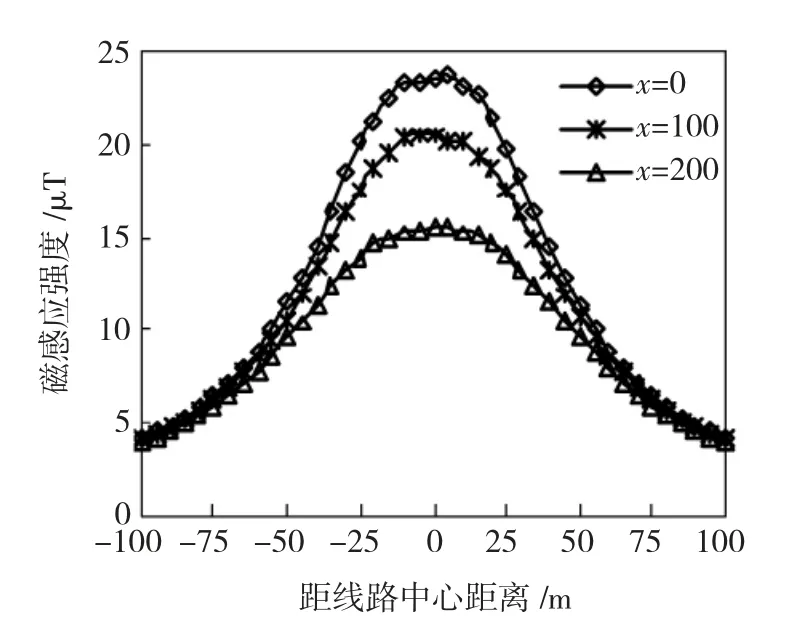
圖7 考慮導線弧垂工頻磁場橫向分布(y=1.5)Fig.7 Considering sag model(y=1.5)

圖7 反映出線路下方工頻磁場分布的橫向和縱向特征，磁場分布關于線路中心對稱:沿橫向，磁感應強度峰值出現在線路中心;沿縱向，朝導線軸向衰減，磁感應強度最大值出現在輸電線路的弧垂最大處，桿塔處磁感應強度最小。

4.3 兩種三維模型仿真結果比較分析

將圖6與圖7比較，可以總結出長直導線三維模型與考慮導線弧垂三維模型磁場計算結果的異同點:

1)長直導線維模型僅僅能反映出輸電線路磁場橫向變化特點:關于線路中心對稱。

2)考慮導線弧垂三維模型能夠同時反映輸電線路下方磁場的橫向與縱向變化特點，計算所得磁場分布呈軸對稱。沿線路縱向磁感應強度最大值出現在輸電線路弧垂最大處，并且朝兩側方向衰減，桿塔處的磁感應強度最小。

3)在弧垂處，兩種模型計算的磁感應強度一致。

5 結論

本文通過有限元法，對線路模型進行簡化后、直觀地仿真分析了特高壓輸電線路的電磁場。考慮導線弧垂的三維模型能夠同時反映輸電線路下方電磁場的橫向與縱向變化特點，計算所得場強分布呈軸對稱形。沿線路縱向電磁強度最大值出現在輸電線路最大弧垂處，并且朝兩側方向衰減，桿塔處的電磁強度最小。考慮導線弧垂的三維模型能夠更加完整地分析空間中導線周圍電磁場，計算結果更加準確。

[1]鄔雄，萬保權，路遙.1000kV級交流輸電線路電磁環境的研究[J].高電壓技術，2006，32(12):55 －58.WU Xiong，WAN Baoquan，LU Yao.Study on electromagnetic environment for 1000kV AC transmission line[J].High Voltage Engineering，2006，32(12):55 －58.

[2]黃道春，阮江軍，余世峰，等.特高壓緊湊型輸電線路工頻電場強度計算[J].高電壓技術，2006，32(7):69 －71.HUANG Daochun，RUAN Jianjun，YU Shifeng，et al.Calculation of the power frequency eletric field intensity of UHV compact transmission lines[J].High Voltage Engineering，2006，32(7):69－71.

[3]劉振亞.特高壓電網[M].北京:中國經濟出版社，2005.

[4]張利庭，胡白雪，周浩.特高壓輸電線路下方工頻電磁場的研究[J].能源工程，2006(4):49 －53.ZHANG Liting，HU Baixue，ZHOU Hao.Study on the power frequency electromagnetic field under UHV transmission lines[J].Energy Engineering，2006(4):49 －53.

[5]倪光正，楊仕友，錢秀英，等.工程電磁場數值計算(M).北京:機械工業出版社，2004.

[6]黃道春，阮江軍，文武，等.特高壓交流輸電線路電磁環境研究[J].電網技術，2007，31(1):6 －11.HUANG Daochun，RUAN Jianjun，WEN Wu，et al.Study on electromagnetic environment of UHV AC transmission lines[J].Power System Technology，2007，31(1):6 － 11.

[7]牛林，趙建國，李可軍.1000kV特高壓交流輸電線路工頻磁場分析[J].山東大學學報:工學版，2010，40(1):154 －158.NIU Lin，ZHAO Jianguo，LI Ke jun.Study of a power frequency magnetic field of 1000 kV UHV AC transmission lines[J].Journal of Shang Dong University:Engineering Science，2010，40(1):154－158.

[8]WANG Fei，WANG Weijie，JIANG Zhichao.Analysis of the Linefrequency Electric Field Intensity around EHV Transmission[C]//2010 International Conference on Electrical and Control Engineering，June 26 －28，2010，Wuhan，China.2010:3344 － 3346.

[9]高俊吉，劉大明.邊界棱棱邊元 FEM－BEM法在開域靜磁場計算中的應用[J].哈爾濱工程大學學報，2009，30(11):1311－1316.GAO Junji，LIU Daming.Application of an FEM-BEM method based on boundary edge elements to open boundary magnetostatic problems[J].Journal of Harbin Engineering University，2009，30(11):1311－1316.

[10]肖冬萍，何為，張占龍，等.特高壓輸電線工頻磁場三維優化模型[J].中國電機工程學報，2009，29(12):116 －120.XIAO Dongping，HE Wei，ZHANG Zhanlong，et al.Three-dimension optimization model for power frequency magnetic field of UHV transmission lines[J].Proceedings of the CSEE，2009，29(12):116－120.

[11]Maruvada P.Sarama，Jainschewskyj.Electrostatic field of a system of parallel cylindrical conductors[J].IEEE Transactions on Power Apparatus and Systems，1969，88(7):1069 － 1078.

[12]牛林，杜至剛，趙建國.1000kV級交流特高壓輸電線路導線做小對地距離研究[J].電力自動化設備.2008，28(1):17－22.NIU Lin，DU Zhigang，ZHAO Jianguo.Bundle conductor minimum ground clearance of 1000kV AC UHV transmission lines[J].Electric Power Automation Equipment.2008，28(1):17－22.

[13]張宇，鄭偉，文武，阮江軍，等.架空線路分裂導線表面電位梯度的數值計算[J].高電壓技術，2005，31(1):23 －25.ZHANG Yu，ZHENG Wei，WEN Wu，et al.Numerical calculation of electric field intensity on the surface of bundle conductors of overhead transmission lines[J].High Voltage Engineering，2005，31(1):23 －25.

[14]劉振亞.特高壓交流輸電技術研究成果專輯(2008年)[M].北京:中國電力出版社，2009.