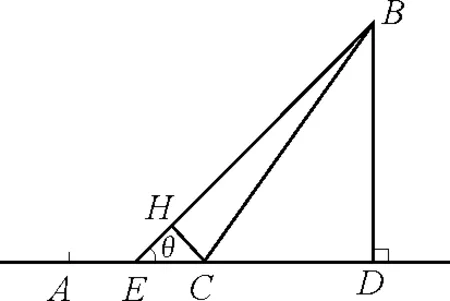
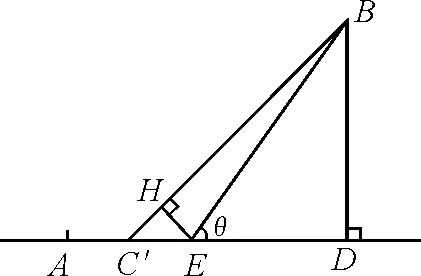
用時最短問題求解五法

張新華

(浙江省天臺中學 浙江 臺州 317200)

一艘漁艇停泊在距岸9 km處，今需派人送信給距漁艇15 km處的海岸漁站，如果送信人步行每小時5 km，船速每小時4 km,問應該在何處登岸，再步行可以使抵達漁站的時間最省？

解法一：矢量分解法

不妨先設人從岸上出發，再跳入水中到達船原來所在的位置，該過程所花的時間與坐船沿相同路徑到岸邊再跑至漁站所花的時間相等．

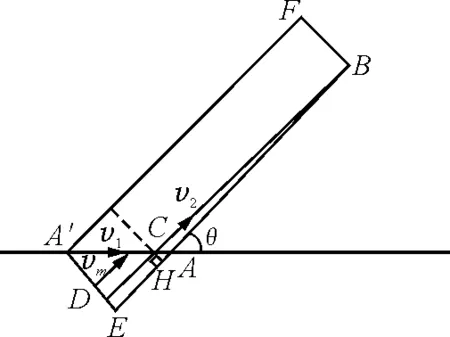
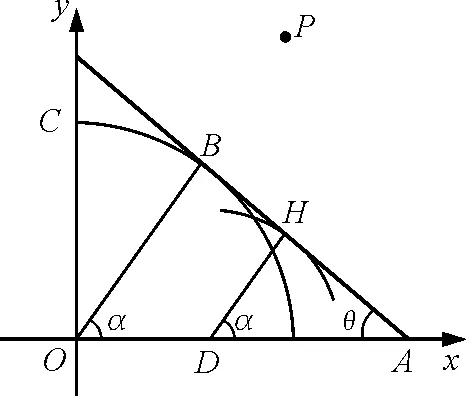
如圖1，A為漁站，B為漁艇原來的位置，AB與岸方向夾角為θ．

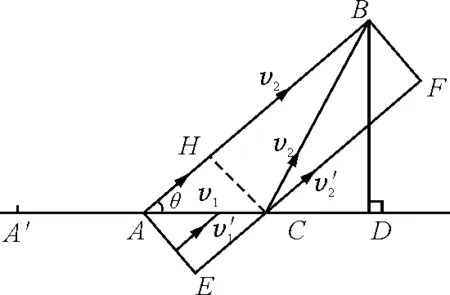
圖1

設人在岸上先經C點，再進入水中．

tAC=tEC

(1)

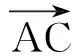
又

故直接從A到B，在AH段所花時間與從E到C(即A到C的分運動)所花時間相等．所以

tAH=tEC

(2)

由式(1)、(2)可知

tAC=tAH

(3)

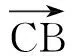
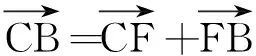
人從C到B所用時間等于從C到F所用時間，即

tCB=tCF

(4)

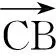
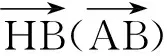
所以tHB

(5)

由式(4)、(5)可知

tHB

(6)

綜上所述

tAHB=tAH+tHB

所以，在本題中選A→H→B的路線(即直航路線)最合適．

有同學會認為本題中直航的走法具有偶然性．若漁站在A點左側A′點(如圖2)，應當怎么走呢？

圖2

答案是先從A′點走到A點，再在A點下水直達B，此時A點是與B連線與岸夾角為θ的點

下面給出證明：

情況一：人過A點后繼續跑，直到C點才下水．那么人在后半段，即A→C→B所花的時間將大于從A直接到B所花的時間．

tA′A=tEA

(7)

若人在C點下水，則其軌跡為A′→C→B，且

tA′C=tD C=tEH

(8)

而由圖可知CB>HB，又因為人在CB段的速度為

v2=4 m/s

在HA段及AB段(即為HB段)的速度也為4 m/s．

所以tCB>tHB

(9)

由式(7)～(9)可知

tA′CB=tA′C+tCB=tEH+tCB>

tEH+tHB=tEA+tAB=tA′A+tAB=tA′AB

綜上可得：結論是tA′AB為最短時間．

解法二：邊界法

如圖3，以岸為x軸，漁站為O點，建立坐標系．

圖3

設經時間Δt，作一以OC=v2Δt為半徑的圓，這是不跑，直接進入水中的一種狀態．再在x軸上作一直線長為OA=v1Δt,這是不跳水，只跑的狀態，兩個狀態均用掉Δt時間．

過A作圓O的切線交于B點，設AB與x軸負方向夾角為θ．

設經時間Δt′(Δt′<Δt)后跳水，則在岸上行OD=v1Δt′，作DH⊥AB，且交AB于H點.則

所以

DH=v2(Δt-Δt′)

而這即是在岸上用掉時間Δt′后，在水中所能游的最大半徑．

又因為該半徑與直線AB垂直，故圓D與AB相切．因為D是任意點，故對所有的0≤Δt′≤Δt，上述結果均成立，故AB是無數個圓組成的包絡線．

而CBA與x軸、y軸圍成的區域即為Δt內可能到達的最大范圍．

又因為CBA是界限，而到達界限是一個臨界狀態，即沖在最前頭．

而到達界限所選擇的路徑恰巧是先在岸上走，再垂直于邊界游，直至到達到目的地．此時所花時間最短(單位時間內能游到最遠處)，而此時在水中游的速度方向與x軸的夾角α滿足

由題意，漁站與漁艇的連線與x軸恰好成α，故直通最省時．

解法三：類比法

由費馬原理可知：光沿光程為極值的路徑傳播．若人所選擇的路線最省時，不妨將人類比為光．

設人在岸上走的速率為v1，在水中的速率為v2．

圖4

如圖4，根據光的折射定律得

所以人進入水后的速度方向與岸的夾角為

即直通最省時．

解法四：求導法

如圖4，設AC=x,則CD=12-x.

在直角△BCD中

則

故總時間

上式中t對x求導后，令t′=0,解得x=0.

故在A處登岸最合適．

解法五：微元法

圖5

如圖5，設A→E→B為最合適的路徑．

在E的右邊取一點C，令EC=Δx且Δx→0

由數學知識可知，tAEB為總時間t是關于x(x=AE)的一個極值．

在極值處，t的導數值為零，故在該處附近，t關于x的變化率為零，即Δt→0.

故人沿ACB行走所花的時間與沿AEB行走所花時間之差Δt=0.

而人從E→C代表在岸上多跑了時間

在水中(C→B)少花的時間可近似為

因

Δt=tEC-tEH=0

故可解得

由題意，直通最合適．

因時間t關于x(x=AE)的函數極值附近有左極限和右極限，以上只證明了其中一個．

對于另一種的討論，請讀者參照圖6自行證明，本文不再贅述．

圖6

點評：

一道題目，五種解法，殊途同歸，各有千秋．

方法一淺顯易懂、思維嚴密，是解決此類問題的“通法”，是重要的物理模型；

方法二受“惠更斯原理”啟發，知識覆蓋面廣，應用靈活；

方法三思路清晰，運算量少，體現了類比的思想方法；

方法四體現了導數強有力的“工具性”，也是一種十分可取的方法；

方法五體現了微元的思想，與方法四原理類似，但運算量大大減小．

由此可見，本題的五種解法對培養學生發散性的思維能力，強化對知識的應用能力都大有裨益．