巧用橢圓軌道推導引力勢能公式
吳好
(江蘇省鎮江中學 江蘇 鎮江 212017)
引力勢能公式的推導在物理思想上通常是利用引力做功等于引力勢能變化的負值得出.由于引力是變力,在計算引力做功時,在數學方法上通常是用積分運算.在高中將其作為拓展內容給學生介紹時,一般是將物體的位移分成許多小段,將每一小段的引力看成“恒力”,將每一小段“恒力”做的功求和得出引力做的總功,這在本質上還是積分運算.
能否用其他的方法推導出引力勢能的公式呢?通過查閱大量的資料發現所有的書籍講授的方法幾乎都是積分法.直到有一次筆者在解題中,計算了衛星做橢圓軌道運動經過近地點和遠地點的速度的數值,在此基礎上做了進一步的思考,用橢圓軌道將衛星從低圓軌道送到高圓軌道的過程中,衛星在近地點和遠地點的兩次加速所增加的動能等于衛星在兩個軌道之間的能量差,如果能夠設法求出這個能量差,再設高圓軌道的半徑為“無窮大”,就能得到衛星在圓軌道的能量,利用衛星的勢能加上動能等于衛星的總能量就能夠得出衛星的引力勢能公式.
推導的思路是,先得出衛星以兩個不同的半徑做圓周運動的速度表達式,設法求出橢圓軌道長軸頂點的曲率圓半徑,再根據引力提供向心力,給出衛星與這兩個不同的圓軌道相切的橢圓軌道近地點和遠地點的速度,求出兩個圓軌道間的能量差,在此基礎上推導出引力勢能公式.
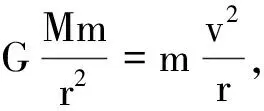
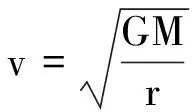
(1)
1 橢圓的相關數學知識
如圖1所示,橢圓長軸是2a,短軸是2b,焦距是2c,則
a2=b2+c2
(2)
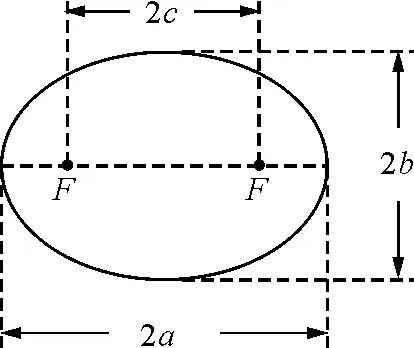
圖1
2 橢圓在半長軸和半短軸處的曲率圓半徑
為求橢圓在長軸和短軸頂點處的曲率圓半徑,我們將水平面的勻速圓周運動投影得到傾角為θ的斜面上 ,如圖2所示.半徑為b的圓,投影到斜面上得到的橢圓半長軸為a,半短軸為b,顯然滿足①
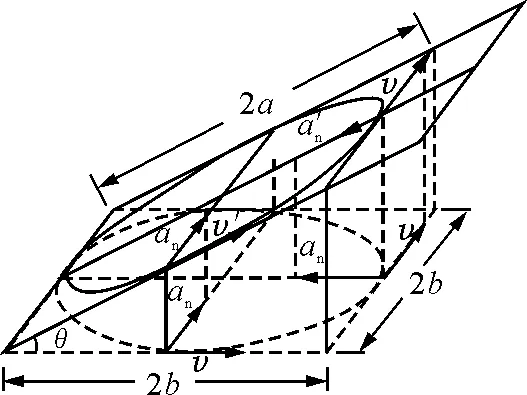
圖2
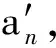
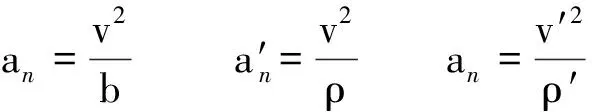
解以上各式容易得出長軸頂點處的曲率圓半徑為
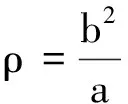
(3)
短軸頂點處的曲率圓半徑為
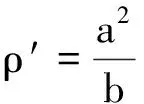
(4)
式(3)和式(4)與解析幾何學中所得到的結果一致.實際上橢圓在長軸和短軸處的曲率圓半徑只要求出一處,另一處的曲率圓半徑可以將原來的長軸看成短軸,短軸看成長軸得出.
3 衛星在近地點 A和遠地點B的速率
衛星做橢圓運動,此時地球中心為橢圓的一個焦點,如圖3所示.衛星近地點距地心的距離為(a-c),遠地點距地心的距離為(a+c);衛星在近地點的速度為vA,遠地點的速度為vB,在近地點和遠地點瞬時做圓周運動的半徑(曲率圓半徑)為ρ.衛星在A,B點瞬時做圓周運動的向心力由萬有引力提供,可以得出
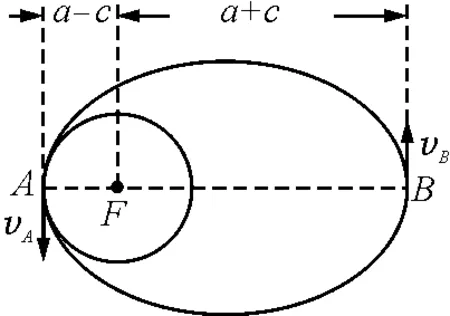
圖3
在近地點A
(5)
在遠地點B
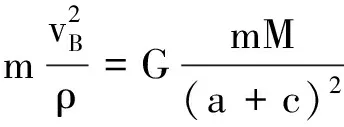
(6)
將式(3)代入式(5)和式(6)得到
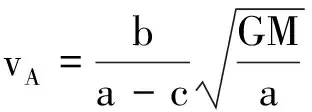
(7)
(8)
4 引力勢能公式的推導
設人造衛星繞地球做圓周運動的軌道半徑分別為r1和r2,如圖4所示.將衛星從圓軌道“1”送到圓軌道“2”上,通過橢圓軌道在近地點“A”設法將衛星的速度由v1增加到vA,在遠地點將衛星的速度由vB增加到v2.衛星總能量的增加就是兩次動能的增加,設衛星在軌道“1”和“2”的機械能分別為E1和E2
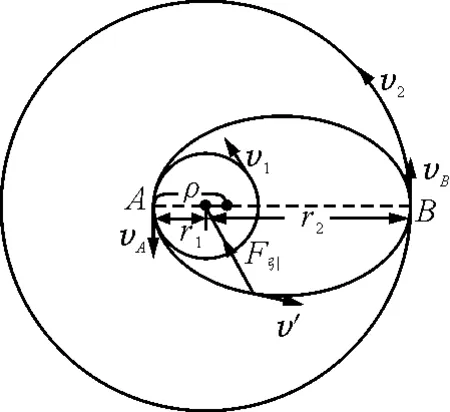
圖4
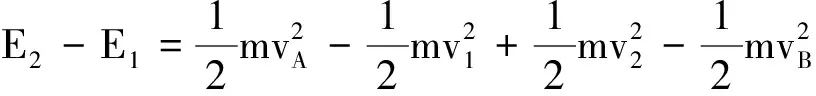
(9)
a-c=r1
(10)
a+c=r2
(11)
聯立式(2)和式(7)~(11)得到
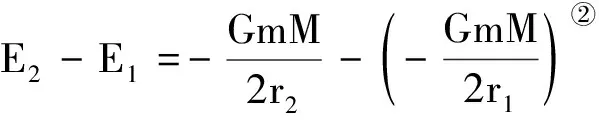
(12)
式(12)中若衛星做圓軌道的半徑足夠大,即r2→∞,并規定衛星距地球無窮遠處能量為零,得到衛星在軌道1的能量為

(13)
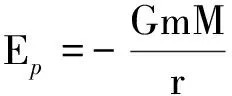
(14)
也可以求出衛星做橢圓軌道的總能量為
(15)
聯立式(1)、(2)、(7)、(10)、(13)、(15)得到
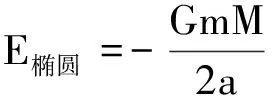
(16)
利用衛星做橢圓軌道運動的臨界條件也可以推導出引力勢能公式.
將式(3)改寫成
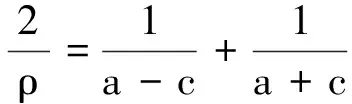
(17)
衛星做橢圓軌道的臨界條件是遠地點趨于無窮遠,即
a+c→∞
此時曲率圓半徑為
ρ0=2(a-c)
將式(10)代入得到
ρ0=2r1
在圖4中近地點發射人造衛星,設與“臨界條件”對應的發射速度為v0,根據引力提供向心力得到
所以
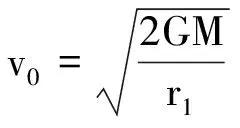
(18)
從式(2)可以看出,當r2=a+c→∞時,衛星做圓軌道的速度為零,而由橢圓軌道遠地點到圓軌道要加速,所以,此時衛星在遠地點的速度為零,衛星在遠地點的機械能為零,根據機械能守恒得到
將式(18)代入得到
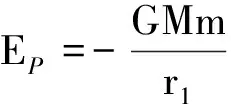
由于r1可以是任意值,就得到了引力勢能的一般表達式(14).
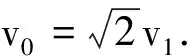
5 結語
值得說明的是,本文作為推導引力勢能的一種方法雖然不是從變力做功的關系得出,但仍然是通過功能關系得出的,因此,并不是發現了一種本質上完全不同的方法,但由于它只用到初等數學,同時又具有豐富的物理內容而顯得非常有趣,對于學生正確運用曲率圓半徑解決問題,加深對衛星做橢圓軌道運動的理解很有幫助.橢圓軌道一但給定,其能量關系就確定了,所以,可以根據橢圓軌道推導出引力勢能公式.
再就文中的“ρ0=2r1”做出說明,衛星在橢圓軌道運行時,由于地心是其中的一個焦點,所以,衛星在近地點以不同的速度發射時,(a-c)即r1為定值,速度越大,(a+c)即r2越大,當a+c→∞時,不能簡單地以為此時c=a,實際上c與a同時趨于無窮大,但(a-c)=r1為定值.
①
建立如圖5所示的坐標系xOy以及x′O′y′,xOy平面內任意一點的坐標(x,y)投影到x′O′y′平面上的坐標為(x′,y′),
滿足
xOy平面內圓的方程為x2+y2=b2
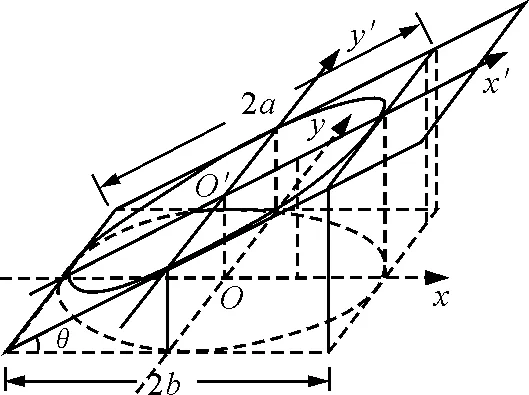
圖5
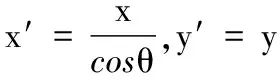
x′cosθ2+y′2=b2
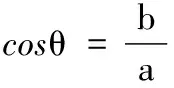
所以,xOy平面內的圓在x′O′y′平面上的投影為半長軸為a,半短軸為b的橢圓.
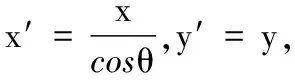
圖2中xOy平面內質點做勻速圓周運動平行于y軸的速度矢量v,在x′O′y′平面內的投影在長軸的頂點大小仍為
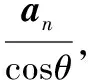
②
(1)詳細的化簡過程
將r1和r2以及式(10)和式(11)代入式(1)式得
再將v1和v2以及式(7)、(8)代入式(9)得
E2-E1=
將式(2)代入并利用式(10)和式(11)化簡得
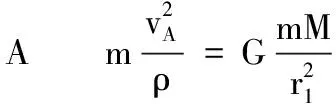
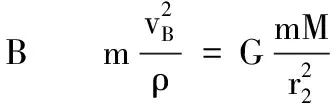
所以
代入上式得到

