洛倫茲吸引子相圖的簡易實現

晏志武

(臨滄市臨翔區第一中學 云南 臨滄 677000)

愛德華·洛倫茲在20世紀60年代根據流體力學中的納維葉·斯托克斯方程、熱傳導方程和連續性方程得出了一組氣象學微分方程.這是一組毫不起眼的方程，但洛倫茲所采用的電腦數值計算和繪制相圖的方法卻影響深遠.這組方程后來被命名為洛倫茲吸引子，因其中的一張典型相圖酷似蝴蝶又被稱為“洛倫茲的蝴蝶”.洛倫茲以此開創了計算機研究復雜非線性問題的先河.

1 洛倫茲微分方程組

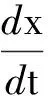
2 微分方程組轉化為差分方程組

現在普遍使用的數學運算軟件是Matlab或Mathematica ，二者都要求具備比較好的數學基礎和編程能力.筆者設想使用Flash動畫軟件實現上述方程組的計算和繪圖，但Flash處理不了微分方程，因此，要先將微分方程組轉化為下列差分方程組

Δx=-σ(x-y)Δt

Δy=(rx-y-xz)Δt

Δz=(-bz+xy)Δt

我們知道，當變量Δt→0時，差分就變成微分了.實際計算時只要Δt足夠小即可取得誤差符合要求的結果.

3 Flash簡單編程實現

程序共有2個圖層、3幀.

(1)第1圖層第1幀放置1個斜二側作圖實例itnpoint(這其實就是一個大小合適的黑色圓點元件分身)，1個變量名為r的輸入文本框和1個控制程序運行或暫停的按鈕，第2，第3幀均為普通幀.

(2)第2圖層為代碼層

第1幀(關鍵幀)設定初值

σ=9;

b=3;

if(_root.r==undefined){r=27};// r的默認值為27，可通過第1圖層的輸入文本框改設為其他值.

else{r=r}

x=1;

y=0;

z=0;

Δt=0.005;//Δt足夠小時，差分方程的運算結果才能充分地近似于微分方程.

第2幀(關鍵幀)迭代運算和繪圖：

hx.moveTo(t, 90+x); // 以下3行設置分量圖繪圖實例hx，hy，hz的初始位置，t是時間值.

hy.moveTo(t, 170+y);

hz.moveTo(t, 250+z);

Δx=-9*(x-y)*Δt; // 以下3行計算差分值.

Δy=(r*x-y-x*z)*Δt;

Δz=(-3*z+x*y)*Δt;

x=x+Δx; // 以下3行完成迭代.

y=y+Δy;

z=z+Δz;

x1=x+(1/2)*y*Math.cos(Math.PI/4); // 以下2行計算“斜二側作圖法”的位置坐標.

y1=(1/2)*y*Math.sin(Math.PI/4);

t=Δt*m; // 更新時間值.

m=m+1; // 記錄迭代次數.

hx.lineTo(t, 90+x); // 以下3行完成第1次以x，y，z為縱坐標，t為橫坐標的分量圖繪制.

hy.lineTo(t, 170+y);

hz.lineTo(t, 250+z);

ht = "ht0" add m; // 生成斜二側圖繪圖點.

duplicateMovieClip("itnpoint",ht,m); // 復制繪圖實例itnpoint (itnpoint放置于第1圖層).

setProperty(bn, _x, x1 ); // 以下2行設置繪圖點坐標.

setProperty(bn, _y, y1 );

第3幀(關鍵幀)：

gotoAndPlay(2); // 回到第2幀作重復地迭代計算.

4 相圖和分量圖舉例

系數σ，b和變量x，y，z的初值確定，r取不同的值將得到顯著不同的圖形見表1，由此可以看到方程組對r的高度敏感性.

表1r取不同值對應的圖形

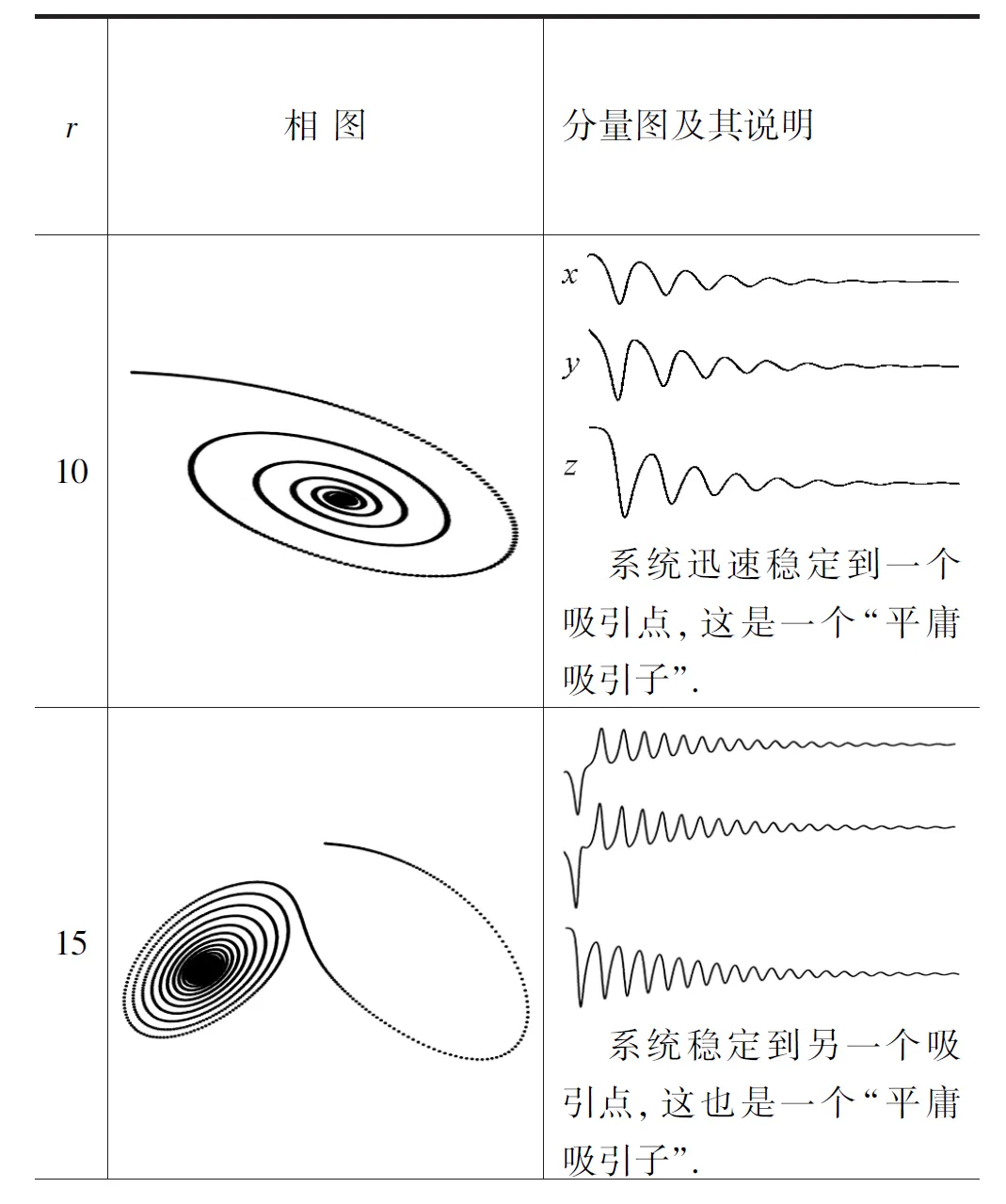
續表

5 結束語

Flash是目前主流的平面動畫軟件，大家比較熟悉.除用于網頁制作外，也可用于數值計算和相圖繪制.其優點是簡單易懂,過程清晰可見，不足之處是運行時間稍長(約需幾分鐘).這種方法尤其適合于數學基礎和編程能力都比較欠缺的中學生進行中學物理與大學物理銜接段的學習.

另外，“洛倫茲吸引子”提醒我們要極其慎重地對待地球環境，輕率地改變它有可能導致難以預料和無法挽回的后果.

參考文獻

1 郝柏林.從拋物線談起 — 混沌動力學引論. 上海：上海科技教育出版社，1993.9

2 劉正君.MATLAB科學計算與可視化仿真.北京：電子工業出版社，2009

3 吳明哲，等.網頁高手-Action程序設計篇.北京：中國鐵道出版社