2012年高考一道靜電場(chǎng)選擇題的解法蠡探*

葉玉琴

(安慶市第二中學(xué) 安徽 安慶 246000)

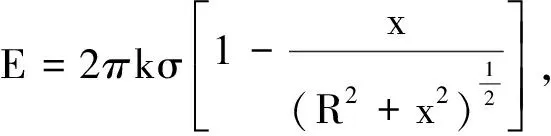
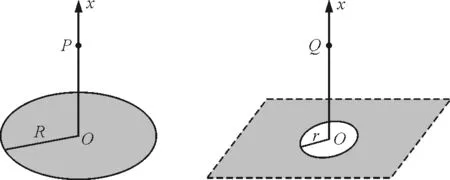
圖1 圖2

解法1 ： 極端分析法

本題考查庫(kù)侖定律及電場(chǎng)強(qiáng)度的疊加原理在靜電場(chǎng)類問(wèn)題中的應(yīng)用.高中階段要求學(xué)生重點(diǎn)掌握點(diǎn)電荷的場(chǎng)強(qiáng)及疊加，而本題處理的是非點(diǎn)電荷類的情形，因此,應(yīng)用高中階段通常的方法無(wú)法求解.本題可以讓考生從高中物理的理想模型入手,采用極端假設(shè)來(lái)求解.

一方面，由題給條件已知半徑為R的均勻帶電圓形平板，單位面積帶電荷量為σ，其軸線上任意一點(diǎn)P(坐標(biāo)為x)的電場(chǎng)強(qiáng)度為

方向沿x軸.對(duì)其進(jìn)行極端假設(shè)，若R→,均勻帶電圓形平板則相當(dāng)于無(wú)限大均勻帶電平板，P點(diǎn)場(chǎng)強(qiáng)則為EP=2πkσ，其大小與P點(diǎn)坐標(biāo)無(wú)關(guān)，方向垂直平板.另一方面，考慮單位面積帶電荷量為σ0的無(wú)限大均勻帶電平板，從其中間挖去一半徑為r的圓板，也進(jìn)行極端假設(shè)，若r→0，類比P點(diǎn)場(chǎng)強(qiáng)，則Q點(diǎn)場(chǎng)強(qiáng)應(yīng)為EQ=2πkσ0.

將r=0代入A，B，C和D四個(gè)選項(xiàng)表達(dá)式，可見(jiàn)，只有選項(xiàng)A與EQ=2πkσ0一致，故選項(xiàng)A正確.

點(diǎn)評(píng)：在物理學(xué)研究中，將復(fù)雜問(wèn)題簡(jiǎn)單化，實(shí)際問(wèn)題理想化，是解決物理問(wèn)題的重要思想方法，本題就是引導(dǎo)學(xué)生關(guān)注科學(xué)思想方法的體現(xiàn)，應(yīng)該說(shuō)不失為一道考查學(xué)生推理能力、思維能力和物理思維策略的好題.

解法2：物理分析法[1]

單位面積帶電荷量為σ0的無(wú)限大均勻帶電平板，從其中間挖去一半徑為r的圓板，則圓孔軸線上任意一點(diǎn)Q(坐標(biāo)為x)的電場(chǎng)強(qiáng)度E為可視作單位面積帶電荷量為σ0的無(wú)限大均勻帶電平板在Q點(diǎn)的場(chǎng)強(qiáng)E1與單位面積帶電荷量為σ0，半徑為r的圓板在Q點(diǎn)的場(chǎng)強(qiáng)E2的矢量之差，即E=E1-E2.

(1)求E1

單位面積帶電荷量為σ0的無(wú)限大均勻帶電平板屬于無(wú)窮大帶電體，不妨假設(shè)其帶正電.根據(jù)對(duì)稱性可知,平板兩側(cè)距平板等距離的點(diǎn)場(chǎng)強(qiáng)大小相等，方向處處與平板垂直，并指向兩側(cè)，如圖3所示.根據(jù)場(chǎng)強(qiáng)分布的以上特點(diǎn)，應(yīng)選取這樣的高斯面即一個(gè)圓柱體的表面，其側(cè)面與平板垂直，兩底面與平板平行且關(guān)于平板帶電面對(duì)稱，如圖4所示，通過(guò)此高斯面的電通量為

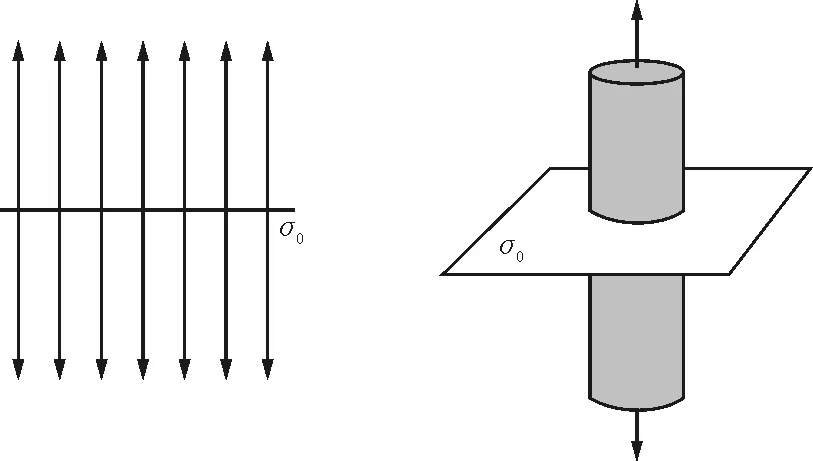
圖3 圖4

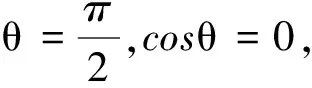
另一方面，此高斯面中所包圍的電荷為πr2σ0,根據(jù)高斯定理有

ΦE=2πr2E=4πkπr2σ0

故E1=2πkσ0

(1)

(2)求E2

根據(jù)題給條件可直接得出單位面積帶電荷量為σ0，半徑為r的均勻帶電圓形平板，在其軸線上點(diǎn)Q(坐標(biāo)為x)的電場(chǎng)強(qiáng)度為

方向沿x軸.也可以由庫(kù)侖定律和電場(chǎng)強(qiáng)度的疊加原理求出，下面給出具體求解過(guò)程.

在圓板上任意半徑為R處，選取圓環(huán)(R+dR)，如圖5所示，則圓環(huán)在Q的場(chǎng)強(qiáng)為

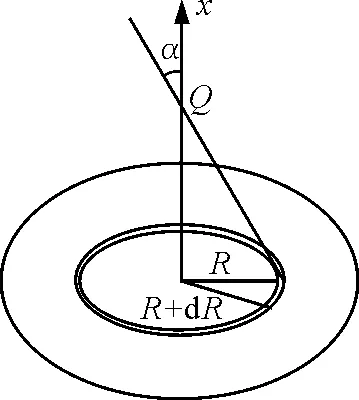
圖5

所以圓板在Q點(diǎn)的場(chǎng)強(qiáng)E2為

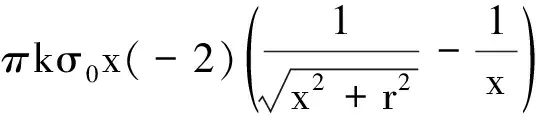
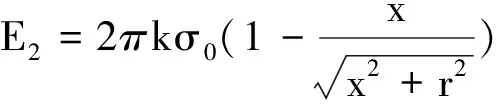
(2)

(3)求E

由式(1)、(2)聯(lián)立易得

點(diǎn)評(píng):此解法運(yùn)用高斯定理、庫(kù)侖定律以及場(chǎng)強(qiáng)的疊加原理進(jìn)行了定量研究，得到了與極端假設(shè)法完全一致的結(jié)果，使問(wèn)題的探討更深入、更到位，也體現(xiàn)了物理學(xué)的簡(jiǎn)潔美、對(duì)稱美、嚴(yán)謹(jǐn)美.

新課程呼喚新教師，隨著新一輪課程改革的不斷深入，新課程教學(xué)對(duì)教師的要求也在不斷提高.物理教師應(yīng)靜下心讀書(shū)，潛下心來(lái)育人，成為科研型教師.在物理教學(xué)中通過(guò)對(duì)物理問(wèn)題的分析，既要注重培養(yǎng)學(xué)生的物理學(xué)科5個(gè)方面的能力，更要注重引導(dǎo)學(xué)生關(guān)注物理思想方法，只有這樣才能在實(shí)踐新課標(biāo)的課堂教學(xué)中促進(jìn)學(xué)生素質(zhì)的提高，才能更好地履行新課程賦予我們的新使命.

參考文獻(xiàn)

1 趙凱華，陳煦謀 .高等學(xué)校教材電磁學(xué).北京：高等教育出版社,1986