立足“最近發展區”設計“追問”的策略初探

柏楊 翟元國

(揚州大學附屬中學 江蘇 揚州 225002)(揚州大學附屬中學 江蘇 揚州 225002)

蘇聯教育家維果茨基認為：教育對學生的發展能起到主導作用和促進作用，但需要確定學生發展的兩種水平,一種是已經達到的發展水平；另一種是可能達到的發展水平，表現為“學生還不能獨立地完成任務，但在成人的幫助下，在集體活動中，通過模仿，卻能夠完成這些任務”.這兩種水平之間的距離，就是“最近發展區”.

由此可見，當教學內容處于其“最近發展區”時，教學不僅可行而且有效,有效教學的標志，就是不斷地把學生的“最近發展區”轉換為“現有發展水平”，也就是不斷地創造新的更高水準的“最近發展區”.在“最近發展區”的不斷升級中，學生的積極性得到調動，潛能得到發揮，實現教育對學生發展的主導作用和促進作用.

以問題為中心的課堂教學，應立足“最近發展區”，用追問的形式，有效幫助學生走過“最近發展區”.追問并不是說隨意提出一串雜亂無章、令人眼花繚亂的問題，而應機智靈活地提出由淺入深、由易到難、循序漸進的多個問題，體現出明顯的程序性；追問的問題難度不等、相對獨立，卻又環環相扣、依序遞進，可以促使學生在一個又一個問題解答的過程中，由表及里、由淺入深地認識事物的本質，實現從已經達到的發展水平提升到可能達到的發展水平.那么，如何立足于學生的“最近發展區”進行 “追問” 設計呢？筆者結合近兩年的四節獲獎課例，談談“追問”的策略.

1 以故引新在追問中實現問題的發展

教學實踐中我們感到，在新授課中，教師能以學生為主體，設立問題情境，充分借助學生已有的發展水平，立足“最近發展區”，通過有序的追問，能不斷激發學生學習熱情，促進學生積極思考，使課堂充滿活力，在“追問”中實現問題的發展.

教學片斷1：教科版普通高中物理必修2，“曲線運動”一節中關于物體做曲線運動的條件探究教學.

情境：觀察嫦娥探月衛星的發射升空和奔月的模擬視頻.

問題：發射火箭點火后，先做什么運動？進入軌道后做什么運動？

回答：先做直線運動，后做曲線運動.(已經達到的發展水平)

追問：物體做曲線運動的條件是什么呢？(將達到的發展水平)

為能拓展學生的思路，教師做了兩個演示實驗：①單擺的運動；②小球平拋運動.

追問：上述兩例中有什么共同之處？要求學生畫出上述兩個實驗中小球的受力分析示意圖，并標出任一時刻的速度方向.(最近發展區)

在教師的引導下，學生分析、發現,做曲線運動的物體所受合外力的方向與物體運動的方向不在同一條直線上.(完成將達到的發展水平)

追問：能否自主設計實驗證明這一論斷？(問題發展)

學生設計了讓小鋼球從直軌道上滾出，再從磁鐵旁邊滾過，看小鋼球的運動軌跡的實驗.實驗結果是無磁鐵時，小鋼球沿直線運動；有磁鐵時，小鋼球從磁鐵旁邊滾過時，做曲線運動.從而用實驗證明了上述觀點.(完成達到的發展水平)

追問：能否用理論證明這一結論？(問題發展)

提示：牛頓第二運動定律告訴我們什么？(已經達到的發展水平)

追問：能否用牛頓第二定律給出上述實驗的理論解釋呢？(最近發展區)

學生通過理論研究歸納出物體做曲線運動的條件.(完成新的將達到的發展水平)

2 逐級登階在追問中實現知識的發展

在實驗課教學中，通過一個接一個的“追問”和解決，學生的思維被緊緊吸引在對物理問題的探究之中；隨著問題的逐步深入，學生在老師和同學的幫助下拾階而上，順利的從已有發展水平到達可能達到的發展水平，在追問中實現知識的發展.

教學片段2：教科版普通高中物理選修3-3第一章第二節“用油膜法測油酸分子的大小”

問題：給你一把直尺，如何能較為準確地測出一張紙的厚度？(構建物理情境)

解決：測多算少.(已經達到的發展水平)

追問：分子的線度大約是10-10m，你有什么辦法測出一個分子線度嗎？(將達到的發展水平)

解決：讓1億個分子緊密排成一排，測出寬度，除以108，得出一個分子的大小.

追問：怎樣才能將1億個分子緊密排成一排呢？(最近發展區)

學生茫然.為幫助學生走進最近發展區，老師設計新的問題來引導學生思考.

問題：有一瓶沙子，體積約為V=1 L，已知每粒沙子的直徑約為d=0.5 mm，如果要把沙子一粒緊挨著一粒平鋪到水平面上，則平鋪面積有多大？(構建物理情境)

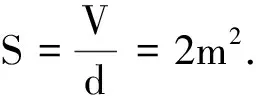
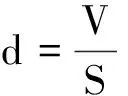
追問：水分子的直徑約為D=0.40 nm，若把水分子看成是球形的，那么,質量為1 g的水的所有水分子一個緊挨著一個緊密平鋪，面積約為多少平方米？(最近發展區)

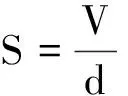
代入數據得

S=2 500 m2生驚嘆，面積有這么大！

追問：在現有的實驗室里，有量筒、刻度尺，怎樣粗略測定分子的大小？(將達到的發展水平)

討論：取很少的水，如為0.01 mg的水，則面積約為250 cm2.

追問：怎么取0.01 mg的水？學生交流討論，有人提出用極細的針頭滴一滴來獲取.

追問：即使能取得0.01 mg的水，怎么才能得到單分子層的水膜？

學生茫然無措.老師提示學生閱讀教材.(最近發展區)

追問：教材中介紹了用油酸粗略測定分子直徑的科學依據是什么？

討論：結合化學課學到的知識，油酸(C17H33-COOH)雖然不溶于水，但其中的羧基具有親水性，而烴鏈具有親油性，所以，當油酸滴到水面時，每一個油酸分子的羧基部分會極力地爭取到與水面接觸而“直立”在水面上，從而完全展開，在水面形成單分子層.

問題：油酸的摩爾質量是282 g/mol，密度約為0.6 g/cm3，要想得到約250 cm2左右的油酸單分子層面積，約需要多少g的油酸？

解決：通過計算可知約為0.002 mg.生驚呼！太小了，無法取.

追問：怎么辦？(更高一級將達到的發展水平)

解決：學生再次展開激烈的討論，提出用稀釋的方案.將油酸溶于酒精，制成油酸酒精溶液.……

追問：油酸和水都是無色的液體，怎么找出油酸的面積呢？……

3 變式拓展在追問中實現方法的發展

在習題課教學中，從學生已有發展區出發，通過變式拓展，將學生的思維引入“最近發展區”，在“追問”中不斷提升，達到更高的發展水平，實現方法的發展.

教學片段3：非線性元件的工作點隨電壓或電流變化的研究

【例題】(2004上海高考物理試卷的第18題)小燈泡燈絲的電阻會隨溫度的升高而變大.某同學為研究這一現象，用實驗得到如下數據(I和U分別為小燈泡上的電流和電壓)：

I/A0.120.210.290.340.380.420.450.470.490.50U/V0.200.400.600.801.001.201.401.601.802.00

(1)畫出實驗電路圖.可用的器材有：電壓表、電流表、滑線變阻器(變化范圍0～10 Ω)、電源、小燈泡、開關、導線若干.

(2)在右圖中畫出小燈泡的U-I曲線.

(3)如果實驗中電池的電動勢是1.5 V，內阻是2.0Ω，問：將本題中的小燈泡接在該電池的兩端，小燈泡的實際功率是多少？(簡要寫出求解過程：若需作圖，可直接畫在第(2)小題方格圖中)

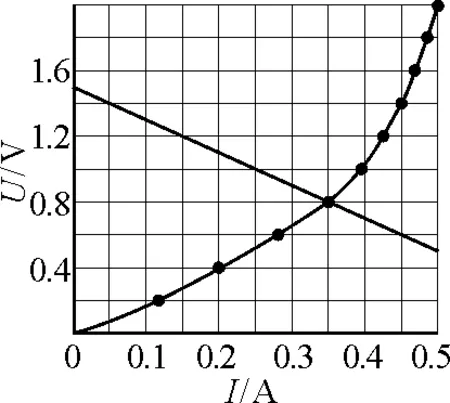
圖1

由于小燈泡的電阻隨溫度的變化不是線性關系，所以，用函數法是難以解決問題的，但利用伏安特性曲線，可以很方便地得到問題的解，只要在上述的U-I圖線上畫出小燈泡伏安特性曲線和電源的外伏安特性曲線，兩圖線的交點，就是小燈泡的工作點，如圖1所示.其交點處的U與I的比值為小燈泡實際電阻，U與I的積為小燈泡的實際功率.教學中我們發現，這個問題學生一般已會解決，但如果將題目的條件稍加變化，學生往往就一籌莫展，其根本原因還是對問題的本質沒有清晰的認識.因此,我們做變式訓練，在追問中實現方法的發展.

追問1：若將兩個一樣的小燈泡并聯接在該電池的兩端，小燈泡的實際功率是多少？(將達到的發展水平)

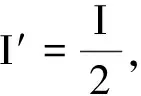
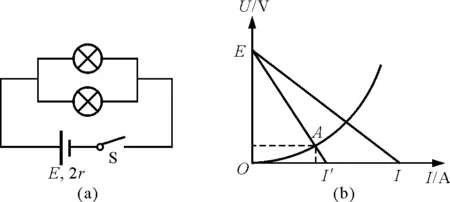
圖2

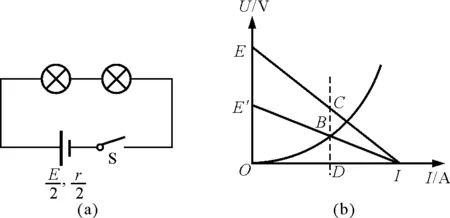
圖3

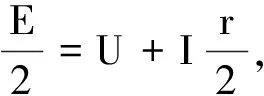
追問3：若一節電動勢為E，內阻為r的電池與一個定值電阻R,小燈泡L組成串聯電路，已知L的伏安特性曲線，小燈泡的實際功率是多少？

方法總結：由以上討論可知，找出非線性元件的工作點問題可以歸納為一個電池和一個燈泡的問題，用E=U+Ir來解決，只要合理地找出等效電動勢和內阻，可以作出電池的外伏安特性曲線與小燈泡伏安特性曲線的交點，可方便地得到小燈泡的實際電壓、電流、電阻和電功率.

4 乘勝追擊在追問中實現能力的發展

在創新設計型實驗的教學中，用“追問”的方法，使學生既聯系了學過的知識，利用已有發展的水平，又能在老師“追問”的主導下，乘勝追擊，開拓、創新，穿越最近發展區，成功到達將達到的發展水平，在追問中實現能力的發展.

教學片段4：電容器的電容概念的建立.

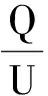
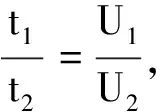
在創新設計型實驗的教學中，通過不斷地追問，學生的物理的問題越來越明確，解決的方案越來越優化，應用知識的水平越來越提高.

參考資料

1 人民教育出版社編輯室.全日制普通高中物理必修2.選修3-1.選修3-3(教科版).北京：人民教育出版社，2003

2 張春興，教育心理學.杭州：浙江教育出版社,第一版.1998.5