多尺度有限元建模及在結構設計中的應用

黃銀燊，袁理明，呂 鵬

(中南建筑設計院股份有限公司，湖北武漢430071)

隨著我國經濟的迅速發展，對建筑結構的功能要求日趨復雜，外觀要求也更加苛刻，這給工程結構設計帶來了巨大的挑戰，結構工程的設計分析也經歷一個迅速發展的階段。一些新的結構形式和結構設計理念不斷提出。精細化分析、精細化設計是目前的趨勢。對于大型的結構一般采用桿系模型、殼、墻等宏觀模型分析結構的整體性能，但是這些模型不能準確模擬結構局部細節的信息，如復雜構件局部應力分布、節點半剛性、節點破壞形態等。對大型結構進行整體精細化實體建模分析，由于計算機條件限制且工作量巨大，是不現實的。因此對關鍵的構件局部和節點的分析，通常的處理方法是將其從宏觀模型中取出，單獨進行精細化的有限元分析，考慮更多的結構細節，如考慮接觸、材料非線性等，為結構設計提供依據。然而，這種二次分析難以準確確定局部模型的邊界條件及其具體的加載形式，而不同的邊界條件對分析的結果影響很大，給判斷分析結果帶來困難［1-2］。而且在往復荷載的作用下，難以判斷局部模型的最不利工況，需要進行多次不同工況組合下的分析。

而在統一的模型下進行結構的多尺度建模計算為上述問題的解決提供了有效的解決方案［3-4］。多尺度計算的應用領域非常廣泛，而對于工程結構而言，多尺度主要考慮采用宏觀與微觀模型相結合的模型，兼顧整體和細部，目前在大跨度橋梁結構分析中應用較多。對于大型結構整體而言，其單元尺寸往往在101m級，而對于細部而言，其特征單元尺寸一般在mm級。結構的多尺度模型首要問題就是解決不同量級尺度下模型的聯接問題，使整體結構的分析和局部細節的分析同步進行，并且考慮到結構材料的局部微細觀尺度上的損傷演化與整體結構之間的相互影響。

本文探討了在ANSYS軟件中進行了結構多尺度建模計算的方法，驗證了微觀模型和宏觀模型之間聯接的準確性，并在一復雜超限高層組合結構的設計中進行了包括復雜節點微觀模型和整體結構模型的多尺度彈塑性時程分析。計算結果表明，多尺度模型可以更準確地模擬結構熱點部位的受力情況，為設計人員對結構性能的把握提供更加豐富的信息。

1 多尺度有限元建模

1.1 界面聯接方式

從工程結構設計角度出發，多尺度建模首先需要根據節點的復雜程度和破壞過程中的非線性程度，選擇適當尺度的分析模型。圖1為精細模型與宏觀模型的聯接示意圖。實際工程中常見的模型組合包括：梁單元與實體(殼)單元聯接、殼單元與實體單元聯接等［5］。由于不同單元模型采用的力學簡化和假設不同，故需要在不同精度模型之間采取適當的聯接方式，達到力的平衡和變形的協調，并且盡量不造成對模型的過分約束。以精細模型為實體單元、宏觀模型為殼單元的聯接來講(剖面如圖1)，恰當的聯接方式應該是，變形后的實體單元和殼單元交界面上各點位移貼合，但是在交界面上各點位移沿平行于該面方向的分量則不能一致。模型界面間轉動自由度的傳遞按照平截面假定。其位移協調條件可以表示為：

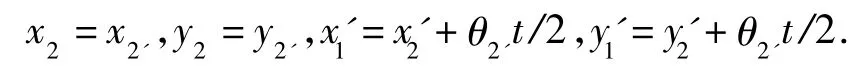
其中為θ2'點的轉角，t為單元厚度。

ANSYS中提供了多種方式進行不同精度單元之間的聯接。一種簡單的方式是，在局部坐標系下將上述條件直接寫成約束方程形式;另外一種方式是對界面處適當的自由度建立剛性聯接(REB2)，在界面區域自動形成約束方程，從節點的位移與主節點始終保持一致，但會導致剛度的增加。上述兩種方式可用于小變形分析。對于大變形問題，ANSYS中提供用多點約束(MPC)方法來進行各不同精度模型的耦合，即用接觸算法來模擬體耦合。這種方法能更好地模擬真實情況，而且使用范圍更廣。MPC方法可以克服傳統接觸算法和ANSYS中的其他多點約束工具的缺點，不需要輸入接觸剛度。對于小變形問題，它代表真實的線性接觸行為，求解系統方程時不需要平衡迭代。對于大變形問題，MPC方程在每個平衡迭代中不斷進行更新，克服了小應變的限制條件。在實際工程中應根據分析目的、模型復雜程度和計算代價等條件選擇適當的約束方法。

圖1 不同尺度模型聯接

1.2 聯接方法算例

在ANSYS軟件中用一個長度為3 m的懸臂矩形鋼梁模型的壓彎加載算例驗證了上述多尺度建模方法的可行性。矩形鋼管梁截面高度為500 mm，寬度350 mm，鋼管壁厚為10 mm。材料應力應變關系采用雙折線模型，初始彈性模量為200 GPa，屈服后硬化模量為3 GPa。建立了4個有限元模型(如圖2)：A模型全部采用殼單元shell181;B模型和C模型均采用多尺度模型，多尺度模型一段采用殼單元shell181，另一段采用梁單元Beam189，界面位置不同(B和C的粱單元分別長0.6 m和1.5 m)，并采用MPC多點約束界面聯接方法;D模型全部采用梁單元Beam189建模。

圖2 驗證模型

加載過程如下：首先在懸臂端沿軸向施加恒定軸壓力20 kN，然后在垂直于梁軸線方向施加豎向荷載P。得到P(豎向荷載)—Δ(頂點位移)曲線，如圖3所示。可見A、B、C三種模型曲線基本完全吻合，而D模型荷載偏小，但結果相差在3%以內，對于工程分析可以忽略。圖4給出了各模型的等效應力云圖，可以看出，多尺度模型B和C殼單元部分的應力分布與A模型吻合較好，在聯接處沒有出現應力集中情況，且保持了變形的協調。仍然采用上述模型，進一步進行了彈塑性動力分析驗證。在懸臂梁的端部添加質量，并考慮鋼梁自身重量，體系阻尼比0.04。輸入單向El Centro NS地震波，分析得到各模型的懸臂端位移反應(Δ)時程曲線，如圖5所示，并與理論計算結果進行了比較。可見各模型的位移反應時程曲線吻合亦令人滿意，位移反應最大值相差在3%以內。

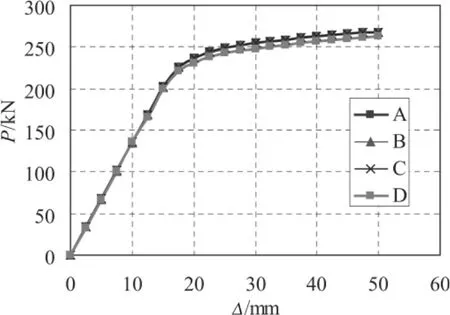
圖3 P—Δ曲線

圖4 等效應力/Pa

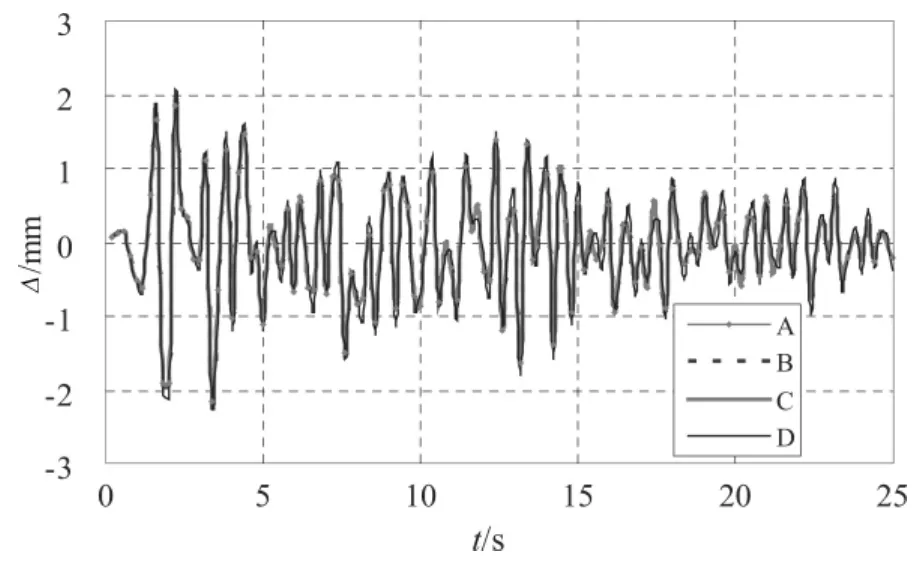
圖5 動力分析結果比較

2 工程應用

在實際工程結構整體分析中，大多采用基于梁、殼、墻模型等宏觀模型進行整體結構非線性有限元計算。采用梁單元建立的模型，在節點部位被簡化為剛性，結構的破壞主要體現為梁柱構件的塑性鉸，而實際上節點本身的破壞在震害中并不少見，“強柱弱梁、節點更強”的設計往往難以實現，且不能經受實際地震的考驗［6］。一般來說，節點部位構造復雜，采用常規的計算方法難以準確得到應力分布、破壞形態等。為了解決上述問題，在一復雜超限連體高層結構設計中，對多個關鍵節點和熱點部位采用實體單元或殼單元精細建模，并進行了彈塑性動力時程分析。

2.1 結構模型

該結構為由兩棟高度不同的塔樓組成的高位連體復雜高層結構，高層塔樓均采用“圓鋼管混凝土柱+H型鋼梁或鋼桁架+鋼筋混凝土核心筒”結構，連接體采用鋼桁架結構。結構主樓和副樓混凝土核心筒均偏置。本結構同時具有扭轉不規則、凹凸不規則、局部夾層、樓板不連續、部分樓層剛度突變、部分樓層承載力突變等超限內容。結構總層數46層，總高度約210 m，整體模型如圖6(a)所示。

連接體桁架設計是本工程設計的關鍵，而其中節點的構造和處理尤為重要。連接體弦桿在多種工況組合下為壓彎或拉彎構件，采用方箱型截面，截面尺寸均為500 mm，最大板厚40 mm。腹桿均采用倒置的 H型鋼度高為500 mm，翼緣寬度500—700 mm，最大板厚60 mm。鋼材選用Q345GJC。在節點中，桿件軸力通過翼緣直接傳至節點板，各軸力匯交于節點板取得平衡。本文選取其中構造最復雜的兩個關鍵節點進行了多尺度的有限元分析。

節點1為連接體主鋼桁架下端與主樓筒體墻體連接部位，桁架弦桿延伸入剪力墻筒體內，墻內設有鋼骨柱，如圖6(b)所示。節點2為連體主桁架中部一復雜鋼節點，如圖6(c)所示。整體模型中用Beam188和 Beam189單元模擬結構桿件，用shell181單元模擬墻體，shell63單元模擬樓板;精細模型中，節點1采用實體單元模擬鋼構件和混凝土，節點2采用彈塑性殼單元模擬鋼板，并植入整體模型中。

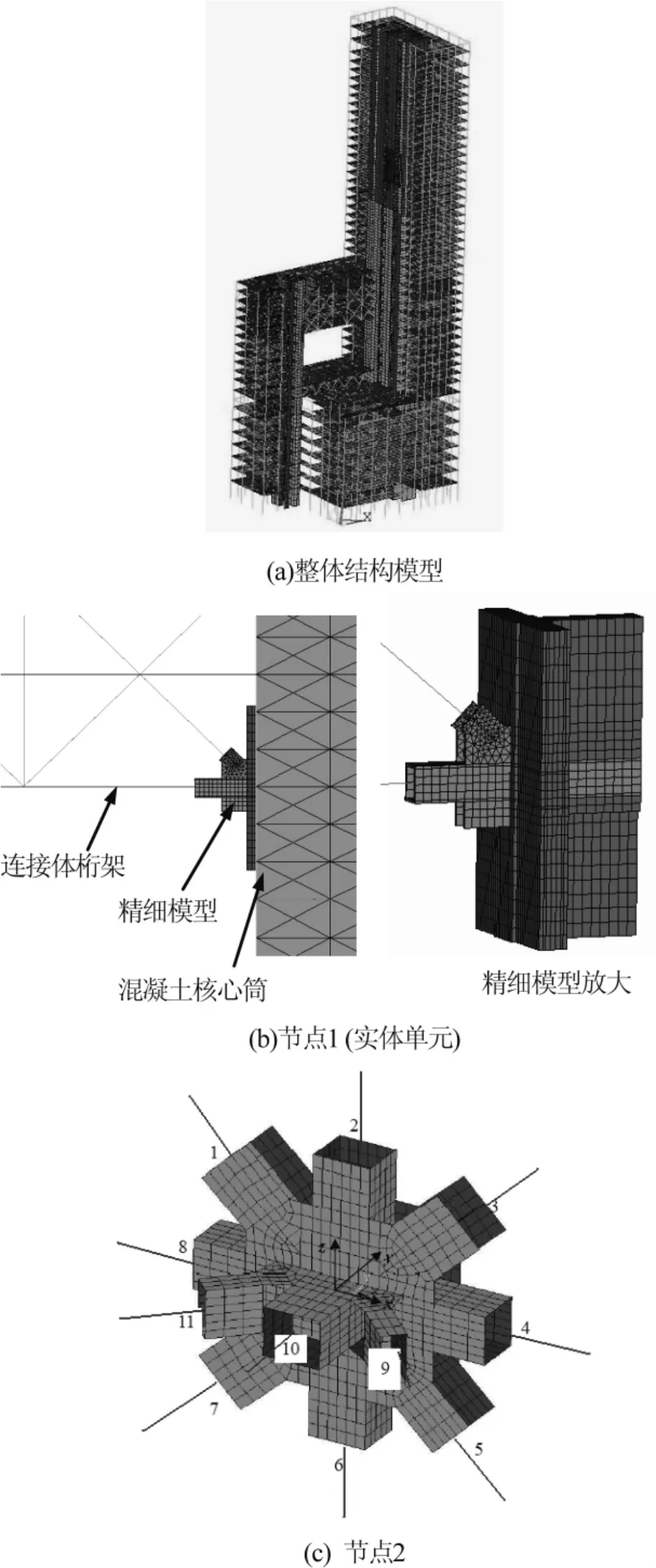
圖6 多尺度結構模型

2.2 分析結果

本文共進行了兩條天然波和一條人工波的大震工況的分析，采用了精細模型分析，時間稍有增加。圖7為節點1某時刻的混凝土豎向應力云圖。由圖7可見，混凝土在與加勁板接觸處壓應力較大，Z向應力超過設計強度，此處混凝土應該合理設計。另外可以發現，節點處鋼材在大震下均未進入塑性狀態，但是連接鋼板轉角處局部應力水平偏高。

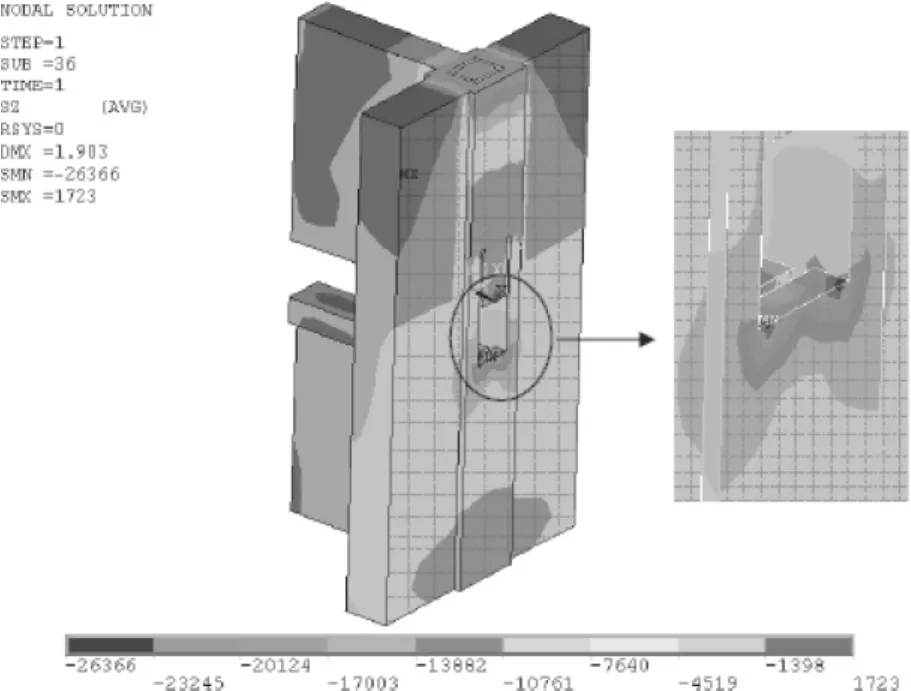
圖7 節點1混凝土豎向應力云圖(kPa)

圖8給出了節點2應力較大時的應力應變圖。分析表明，在大震作用下整個節點大部分都處在較低的應力水平下，而只在某些小范圍局部應力較高甚至進入塑性，但這種局部高應力范圍較小，會隨著施工焊接的的影響而緩解，或者通過應力重分布而緩解，對結構整體的影響不大。

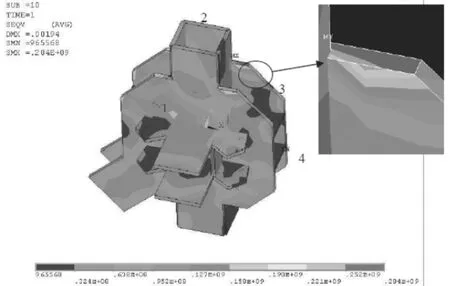
圖8 節點2 Mises應力(Pa)

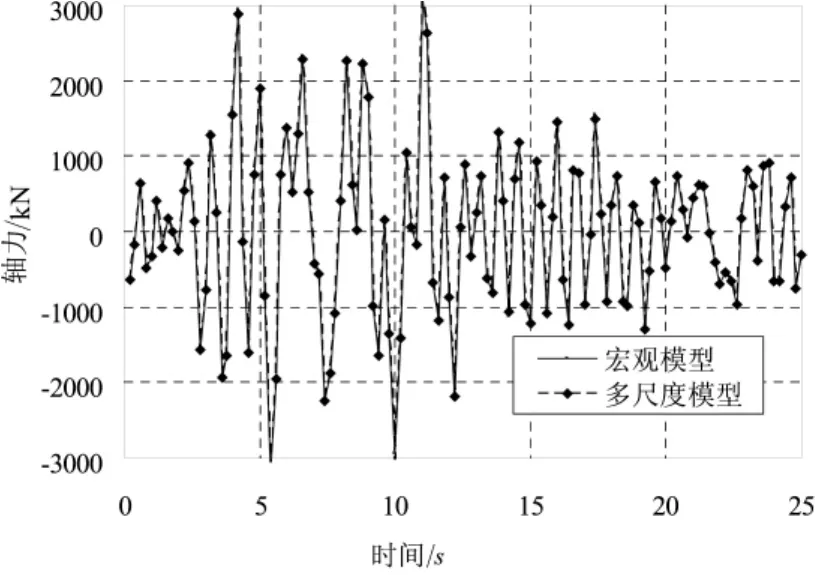
圖9 節點5號桿件2兩種模型桿件軸力時程比較

圖9給出了節點2的5號桿件在整體模型和精細模型在各時刻的桿件內力對比。由圖9可見，兩個模型計算出的桿件軸力基本上完全吻合，因為對于多尺度的精細模型來說，節點的邊界條件在各個時刻和各個工況下都是天然滿足的。采用精細化的模型可以更精確地得到各個時刻的節點應力分布，為節點的設計提供有力依據。

4 結論

3.1 在ANSYS中驗證了不同尺度之間單元的聯接方式，表明可以實現不同尺度模型間的聯接過渡，誤差均在在工程可接受范圍之內。

3.2 在一復雜混合高層結構分析中進行了結構多尺度計算，通過不同尺度單元間的協同，實現了復雜節點微觀模型和整體框架模型的多尺度彈塑性時程計算，計算結果表明，多尺度模型可以更加準確地模擬節點的實際受力情況。

3.3 多尺度有限元計算方法可以在可接受的計算資源和計算時間下，既反應結構的整體性能，又反映結構的局部信息，在結構設計的領域有著較好的應用前景。

［1］ 鄭伯興，黃長華.鋼管相貫節點疑難問題分析及對策探討［J］.鋼結構，2007，22(9)：91-94.

［2］ 陳其業，梁乃剛.多分支管節點的有限元分析［A］.見：中國鋼結構協會海洋鋼結構專業委員會，第一次學術交流論文集.1985.

［3］ 吳佰建，李兆霞，湯可可.大型土木結構多尺度模擬與損傷分析——從材料多尺度到結構多尺度力學［J］.力學進展，2007，37(3)：321-336.

［4］ 陸新征，林旭川，葉列平.多尺度有限元建模方法及其應用［J］.華中科技大學學報(城市科學版)，2008，25(4)：76 ～80.

［5］ 王勖成，邵敏.有限元方法基本原理與數值方法［M］.北京：清華大學出版社，1988年.

［6］ 夏珊，劉愛文.汶川地震框架柱震害的初步分析［J］.震災防御技術，2008，3(3)：237-242.