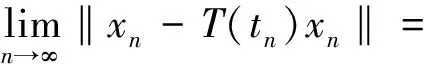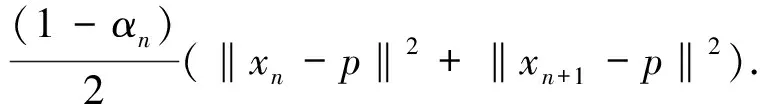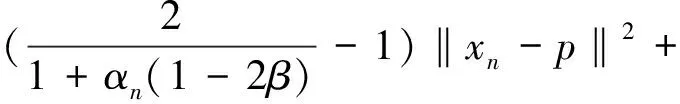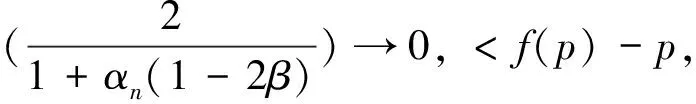非擴張映像顯式迭代序列強收斂性
張學茂
(泰州師范高等專科學校,江蘇 泰州 225300)
研究非擴張映像一個經典方法是利用一系列壓縮映像來直接逼近或迭代逼近非擴張映射的不動點[1].近年來,非擴張映像與漸近擴張非映像在Hilbert空間及Banach空間中的強收斂性,引起了不少專家學者的關注,得到了許多強收斂的條件和證明方法[2-6].受他們的啟發,本文主要利用半閉原理及不動點理論,在具有一致正規結構和一致Gateaux可微范數的Banach空間中給出了關于非擴張映像顯式迭代序列的強收斂性,弱化了非擴張映像顯式迭代序列收斂性的條件,改進和完善了許多學者的證明方法.
1 預備知識
定義1[1]E是一實的Banach空間,C是E中一非空子集映像,f:‖f(x)-f(y)‖≤α‖x-y‖,?x,y∈C,α∈(0,1)則稱f:C→C為一壓縮映像.
定義2[7]?x,y∈C都有‖T(t)x-T(t)y‖≤α‖x-y‖,α∈(0,1)稱T:C→C是非擴張映像.
引理1[8]設E是一實的Banach空間,E*是E的對偶空間,J:E→2E*是由下式定義的正規對偶映像:J(x)={f∈E*:
‖x+y‖2≤‖x‖2+2
引理2[8]設E是一致光滑的Banach空間,C是E的非空閉凸子集,T:C→C是一非擴張映像,且F(T)≠φ,f∈∏C,若定義Q:∏C→F(T),Q(f)=limt-0xt則Q(f)是下列變分式不等式的解
<(I-f)Q(f),J(Q(f)-p)>≤0,
f∈∏C,p∈F(T).
引理3[8]設E是一致光滑的Banach空間,C是E非空有界集,F={T(t):f>0}為壓縮映像?h≥0總有
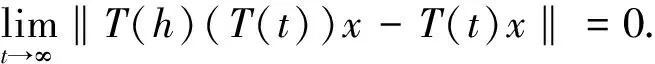
引理4[9]設E是一致凸的Banach空間,C是E一閉凸子集,T:C→C為有不動點的一非擴張映像.若xn→x∈C且(xn-Txn)→y,則(xn-Txn)=y,特別若y=0,則x是T的一個不動點.
引理5[10]設E是一致光滑的Banach空間,T:C→C是有不動點的一非擴張映像.對于任意給定的U∈C,及t∈(0,1),當t→0時壓縮映像Tt:tu+(1-t)T有唯一不動點,則xt∈C強收斂于T的一個不動點.
引理6[10]設E是一致凸的Banach空間,C是E一閉凸子集,T:C→C是有不動點集:F:∩≥0F(T(t))≠φ為非擴張映像,f∈∏k,設{an}?(0,1),β∈[0,1]及{tn}∈R+滿足:


則x0∈k,xn+1=αnf(xn)+(1-αn)T(xn),n=1,2,…強收斂于一不動點T.
引理7[10]設E是一致凸的Banach空間,C是E一閉凸子集,T和S是兩個非擴張映像,F(S)∩F(T)≠?,則F(ST)=F(TS)=F(S)∩F(T).
2 主要結論

xn+1=αnf(xn)+(1-αn)T(tn)xn
,
則該序列{xn}強收斂于F中一不動點P.
證明 第一步證明變分不等式
`首先假設p,q?F都是變分不等式的解,則
. 兩式相減得 ‖p-q‖2-<(f(p)-f(q))(p-q)>≤0, 即‖p-q‖2≤<(f(p)-f(q),j(p-q)>≤α‖p-q‖2,又α∈(0,1),則p=q. 據引理7,再令S=(1-α)I+αU,α∈(0,1),U為非擴張映像.如果Sz≠z則有 ‖Sz-q‖2= 因Tp≠p由定義2有‖p-q‖=‖S(TP)-q‖=‖S(TP)-Sq‖≤‖TP-q‖<‖p-q‖,因此 TP=P,Sp=p, 第二步證{xn}有界,由定義1,引理1和定理中的條件,對于任意序列{xn}∈F, ‖xn+1-xn‖2=<αn(f(xn)-xn)+ 即(1-αnβ)‖xn+1-xn‖2≤0,從而‖xn+1-xn‖→0,所以{xn}一致收斂,則{xn}有界. 由以上證明可知{T(tn)xn}與{f(xn)}有界,由定義1有 ‖T(tn)xn+1-T(tn)xn‖≤‖xn+1-xn‖; ?h>0總有 ‖xn-T(h)xn‖≤‖xn-T(tn)xn‖+ 由引理3可得 第四步證明{xn}強收斂于變分不等式 的唯一解p∈F(t).由引理1、引理6和迭代序列可得 對上式化簡得 J(xn+1-p)>≤0,p∈F(T), 則‖xn+1-p‖2→p. 由引理4、5可得{xn}強收斂于不動點變分不等式的唯一解p. 參考文獻: [1]張石生,楊莉,柳就愛.關于Banach空間非擴張半群的強收斂定理[J].應用與力學,2007(10):1146-1156. [2]趙良才,張石生.Banach空間中非擴張映像不點的粘性逼近[J].數學研究與論,2007(11):919-924. [3]Qing bang Zhang,Cao zong Cheng.Strong convergence theorem for a family of Lipschita pseudocontractive mappings in a Hilbert space[J].Mathematical and Computer Modelling,2007(12):480-485. [4]Yong hong Yao,Rudong Cheng.Convergence to common fixed points of averaged mappings without commutativity assumption in Hilbert spaces[J].Nonlinear Analysis,2006(6):10-16. [5]Naseer Shahzad,Aniefiok Udomene.Fixed point solutions of variational inequalities for asymptotically nonespansive mappings in Banach spaces[J].Nonlinear Analysis,2005(3):558-567. [6]Chang S S.on open questions and approximation solutions of multivalued strongly accretive mappings equations in Banach spaces[J].J math anal appl,1977,216:94-111. [7]T.D.Benavides,G.L.Acedo.H.K.Xu,Construction of sunny nonexpansive retractions in Banach spaces[J].Fixed point theory appl,2005(3):295-305. [8]Xu Hong kun.Viscosity approximation methods for monexpansive mappings [J].J.Math.J,Anal.Appl.,2004,298(1):279-291. [9]Goebel K,Reich S.Uniform Convexity,Hyperbolic Geometry and Nonexpansive Mappings[M].Math Z,1967,100:201-225. [10]Reich S Strong convergence theorems for resolvents of accretive operators in Banach spaces[J].J Math Anal Appl,1980,75:287-292.
‖(1-α)(z-q)+α(Uz-q)‖2=
(1-α)‖z-q‖2+α‖Uz-q‖2-
α(1-α)‖z-Uz‖2≤
(1-α)‖z-q‖2+α‖z-q‖2<‖z-q‖2.
(1-αn)(T(tn)xn-xn),j(xn+1-xn)>=
αn<(f(xn)-xn),j(xn+1-xn)>+
(1-αn)<(T(tn)xn-xn,j(xn+1-xn)>=
αn<(f(xn)-xn),j(xn+1-xn)>+
(1-αn)<(T(tn)xn-T(tn)xn,j(xn+1-xn)>≤
αn‖f(xn)-xn‖‖xn+1-xn‖+(1-αn)
(‖T(tn)xn-T(tn)xn‖‖f(xn+1)-f(xn)‖)≤
αnβ‖xn+1-xn‖2.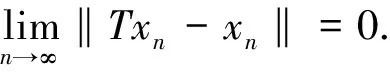
‖f(xn+1)-f(xn)‖≤β‖xn+1-x‖.
‖T(tn)xn-T(h)(T(tn)xn‖+
‖T(h)(T(tn)xn-T(h)xn‖≤
2‖xn-T(tn)xn‖+
‖T(h)(T(tn)xn-T(h)xn‖→0,