“解決問題的策略”之教學策略
2011-12-29 00:00:00陳勇
小學教學參考(數學) 2011年5期
“解決問題的策略”是現行蘇教版數學教材中的新增內容,常用策略有列表、畫圖、列舉、倒推、替換、假設與轉化等。雖然每冊的單元訓練內容量不大,但其中的思維含量與思考價值都相當高。教師必須優化教學策略,讓學生全程參與,自主學習,主動探究。
一、在嘗試中激活解決問題的策略意識
《數學課程標準》中對“解決問題的策略”這類教學內容的要求是:“形成解決問題的一些基本策略,體驗解決問題策略的多樣性,發展實踐能力與創新精神。”這類教學不僅僅是方法的傳授,更是解題思想的滲透。數學課本的教學內容大多是從生活中提煉出來的,教師教學的最終目的應該是“授人以漁”,讓學生在實際學習中體驗到策略的多樣性,激發策略意識,培養學生的創新能力。
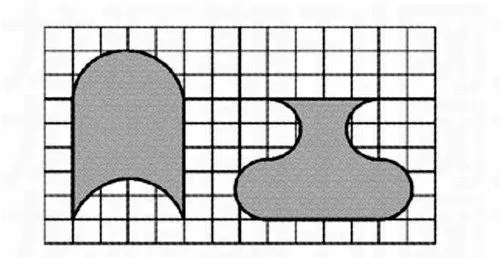
例如,在教學“轉化”這一策略時,出示如下兩個圖形:下面兩個圖形的面積相等嗎?
由于有了數方格及轉化等方面的經驗,學生可能會出現三種比較的方法:(1)通過數方格進行比較;(2)通過分割算面積進行比較;(3)通過圖形轉化的規則進行比較。根據學生的操作方法,組織學生比較得出結論:數方格的方法較麻煩,有些方格不滿,不但數起來麻煩,累加起來也不夠準確;計算面積的方法步驟太多,計算費時又費力,稍不注意還易出錯;而轉化成規則圖形的方法簡潔快捷,兩個形狀不相同的圖形都可以轉化成長5格、寬4格的長方形,面積大小一目了然。通過以上比較,學生很容易體悟到“轉化成規則的圖形”的比較方法更容易掌握,認識到“轉化”策略的優勢,在遇到同類型題目時首選該種方法。這樣,學生解決問題的策略意識也就自然被激活了。
二、在操作探究中掌握解決問題的策略
“授人以魚”只是呈示結果,簡化探索過程。還以上一道題為例,如果教師直接傳授方法:把它們都轉化為長方形來比較,大部分學生都能很快地解決書本上的問題,但此類“轉化方法”并沒有轉化成學生解決問題的方法。教學中,教師要重視引導學生經歷策略形成的全過程,給學生充分觀察、分析、思考及操作探究的空間與時間,讓學生在操作探究中感悟策略的本質,從而掌握解決策略的技能。
又如,在教學“倒推策略”時,教師出示例題目:小明原來有一些郵票,今年又收集了24張,送給小軍30張后,還剩52張。小明原來有多少張郵票?
師:你能根據郵票數量發生的變化,把題目中的條件和問題摘錄下來并進行整理嗎?
學生親歷整理過程,可能出現兩種整理方案:(1)原有?張—→又收集24張—→送給小軍30張—→還剩52張。(2)原有?張—→+24張—→-30張—→還剩52張。
師:你準備用什么策略來解決這個問題?
生1:原有?張←—退還又收集的24張←—跟小軍要回30張←—還剩52張。
生2:原有?張←— -24張←— +30張←— 還剩52張。
由于有了例題的鋪墊,學生經歷了整理過程,感受了數據變化,自然會想到使用“倒推”的策略來解決這個問題。通過操作探究,學生還能體會到第二種整理方案更加清楚明了,而且更加清楚地認識“倒推”策略的本質——從結果出發,尋根求源。
三、在練習反思中發散解決問題的策略
教材中往往依托某一道例題來學習某種解決問題的策略,但例題并不能代表這種策略的全部特征,如果對號入座,無疑扼殺了學生思維的發散性和求異性。
例如,蘇教版六年級下冊教材第71頁例1是圖形的轉化,72頁是回顧一下我們曾用轉化策略解決過哪些問題,73頁例2是分率的轉化等,但在“試一試”中卻出現了計算“1/2+1/4+1/8+1/16”并將算式進行轉化的題目,以及74頁《練習十四》第1題中“將算法轉化”的習題。不少教師在教這部分內容時,常常感到例題與習題是脫節的。其實不然,這些例題與習題都有一個共同的特征:即未知的可以轉化已知的、復雜的可以轉化為簡單的,這才是轉化策略的本質所在。所以它們貌雖不同,解題思想卻是相通的,都可用轉化策略來解決。
教師可引導學生在練習中反思,進行適當的比較與總結,在深刻理解“策略”內涵的基礎上,進一步認識“策略”的外延,逐步優化解決問題的策略。
四、在綜合運用中領略策略的價值
教材中幾種解決問題的策略編排分布具有由單一逐步走向綜合的特點。而在解決實際問題時,往往也是多種策略的綜合運用。如:全班42人去公園劃船,一共租用了10只船。每只大船里坐5人,每只小船里坐3人。租用的大船和小船各有幾只?教材中呈現的策略有畫圖、列表、假設、替換等策略,其中替換策略的理解是這部分內容的重點。不難看出,無論是畫圖策略,還是列表策略,都滲透著替換運用的思想。在解決此類問題時,教師引導學生加強策略的綜合運用,才能讓學生領悟到策略的存在價值——解決問題、指導生活,也才能讓學生在解決實際問題時,自覺地想到用策略來解決問題。
(責編藍天)

