“認識比”教學設計與評析
2011-12-29 00:00:00周昱城
小學教學參考(數學) 2011年5期
教學目標:
1.使學生在具體情境中理解比的意義,掌握比的讀寫方法,知道比的各部分名稱,會求比值。
2.使學生經歷探索比與分數、除法關系的過程,初步理解比與分數、除法的關系,會把比改寫成分數的形式。
3.使學生在活動中培養分析、綜合、抽象、概括等能力,在解決實際問題的過程中,體會數學與生活的聯系,體驗數學學習的樂趣。
教學過程:
一、初步感知
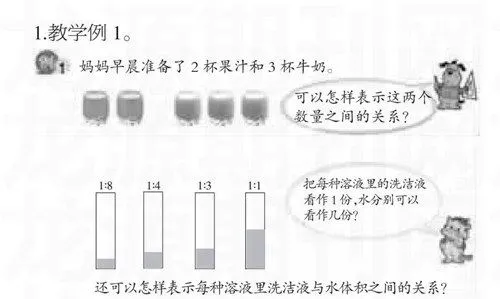
1.教學例1。
師:從例1中你能獲得哪些信息?
生1:有2杯果汁和3杯牛奶。
師:可以怎樣表示這兩個數量之間的關系?
(引導學生回答出:相差關系:牛奶比果汁多1杯,果汁比牛奶少一杯;倍數關系:果汁的杯數相當于牛奶的2/3,牛奶的杯數相當于果汁的3/2
師:這兩個數量之間的關系還可以說成果汁與牛奶杯數的比是2比3,記作2︰3。(板書)除了這樣表示外,還可以怎樣表示?
生2:牛奶與果汁杯數的比是3比2,記作3︰2。
師:都是描述牛奶與果汁杯數的比,為什么上面是2︰3,而下面是3︰2呢?
生3:因為第一次是果汁與牛奶杯數比,而第二次是牛奶與果汁的杯數比。比是有順序的。
2.“試一試”。
(引導學生分析信息,讀懂題意)
生4:第1瓶里的洗潔液看作1份,水為8份。
生5:第1瓶里的水與洗潔液體積比為8︰1。
生6:第1瓶里的洗潔液占水體積的,水是洗潔液體積的8倍。
3.教學例2。
出示:小軍走900米路用了15分鐘,用25元錢購買了4盒餅干。
師:這些數量之間的關系可以用比描述嗎?
引導學生理解:因為路程÷時間=速度,所以可以說小軍走的路程與時間比是900比15,記作900︰15;因為總價÷數量=單價,所以購買餅干的總價與數量的比是25比4,記作25︰4。(板書)
師:能說900比25,15比4嗎?(讓學生認識到兩個有聯系的不同種類的量之間的關系才可以用比描述)
二、深刻理解
1.教學比的各部分名稱。
這些比有什么相同的地方?
師:比號和冒號有什么區別?
2.提煉比的意義。
師:觀察這幾組數量,你認為比與以前學習的什么關系密切?你認為比表示什么意思?(板書:兩個數的比表示兩個數相除)
3.梳理比、除法和分數之間的關系。
出示:3︰5=( )÷( )。
師:如果后面再加一個“=”,你認為可以填什么?
依據上面的算式填寫a︰b =( )÷( )= ( )( )
(利用最后面的括號,使學生明白比的后項不能為0,及其原因)
師:怎樣求一個比的比值?
師:根據分數與比之間的關系,兩個數的比還可以寫成分數的形式。(教學寫法和讀法)
三、整體把握
師:現在你對比有哪些了解?
引導學生小結出:①同種量或者不同種而有聯系的兩個量之間的關系可以用比描述;②比的意義;③比(包括寫成分數形式的比)的寫法,讀法和各部分名稱;④求比值的方法;⑤比與除法、分數之間的關系……
四、運用提升
1.基礎練習(教科書第70頁練一練1~3題)。
2.判斷下面哪個是比?它們與黑板上的比有什么不同?
5 3︰54.8x︰y10/7 5.6︰0.9
3.下列哪些數量之間的關系可以改寫成比的形式?為什么?
7÷165+4 6×721-xy/19 (7+x)÷x
4.求出下列各比的比值,你發現了什么?
6︰7 12︰14 1.2︰0.41/2:1/6
5.出示:
糖與水的質量的比1∶20糖與水的質量的比3∶20
師:你知道哪一杯水甜?為什么?如果要你配一杯比第二杯更甜的糖水,這杯的糖與水的比可能是多少?
評析:
一節數學課的教學設計既要關注學生的認知起點,也要關注教師自身的教學水平和風格;既要關注教學內容,還要關注承載知識的教學素材。作為一節概念課——“認識比”教學設計,在關注以上方面之外,更關注了數學概念課教學的特點。
一、情境經歷中感悟概念內涵
創設情境教學概念能讓學生在不經意中接觸、接納、理解概念。本節課教學首先呈現例題教學情境,從倍數關系過渡到比的關系,之后引導學生在身邊的情境中體會比。例2是含有學生熟悉數量關系的情境,由數量關系作為中介溝通了除法與比之間的聯系,在學生知識的生長點處揭示比的概念內涵,學生會輕松而樂意地cef88064848b8d262f707da1f671346948b812e0d86d410a9ba34f941f5e60a3接納比。學生從不同情境以及它們之間的比較中向比層層靠近,最后脫離情境,丟棄非本質特征,歸納出概念定義(內涵)——兩個數的比表示兩個數相除。在概念鞏固階段教學順序又與此正好相反,先是單純的概念練習,然后在情境中升華概念。
二、變式辨析中拓展概念外延
概念的內涵與外延是一對不可分離的孿生兄弟,在注重概念內涵教學時,不可忽略了概念外延的拓展。例題呈現給學生的都是整數比,因為整數比利于學生理解,是比的概念原型。我們要利用概念原型干擾少的特點,在揭示概念本質特征時發揮其重要作用。但是在鞏固階段也一直使用原型,將會使學生形成定式,僵化學生思維。變式的辨析不僅能打破思維定式,而且能讓學生在不同類別比較中拓展概念外延。所以,在運用提升中設置了第2題,讓學生在辨別比較后,認識到比除了整數比之外,還有分數比和小數比,甚至帶有未知數的式子比。
三、網絡構建中完善概念結構
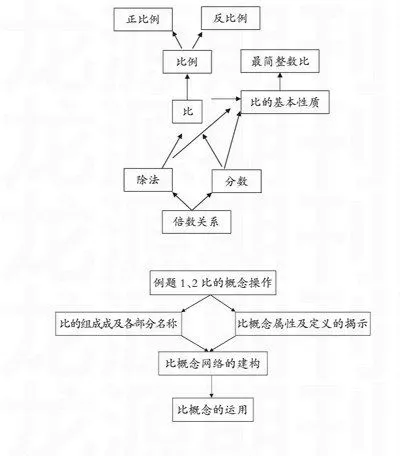
概念教學不能單兵作戰,它應在概念網絡中進行。比這個概念教學在利用學生已有概念網絡的同時,還要為概念網絡的進一步生長作好鋪墊。所以,本節課的教學設計是依據下面的概念網絡進行的。
新授課中運用倍數關系(分數)和除法揭示比的本質特征,然后由它們之間的意義聯系聯想到它們組成部分之間的一一對應關系。這部分是利用已有網絡建構網絡,后面部分是為概念網絡的日后構建打下基礎。運用提升中的第4題,學生通過求比值能輕而易舉地發現6︰7 和12︰14、1.2︰0.4和1/2︰1/6的比值相等,這個發現能很好地為后面的比的基本性質和比例教學埋下伏筆。
四、系統環境下全面把握概念
數學概念系統是指數學概念各個層面。數學概念系統包括概念的本質屬性、定義、形式、概念網絡、概念運用等。比只有在這樣的概念系統中才能被學生全面把握,同時這樣系統的建立,為學生學習其他數學概念建立了學習模式。本課教學設計的概念系統可以用流程圖表示如下:
整個教學設計除了讓學生一直沉浸在比的概念系統中,同時在新授課結束后的整體把握比的環節引導學生完整總結自己(或小組合作完成)對比的認識,讓隱性的概念系統顯現出來,使學生頭腦中比的概念系統更加清晰與明確。
(責編黃桂堅)

