基于標準差準則的海底三維地形模型構建

韓富江，潘勝玲，王德剛，來向華

（1.國家海洋局第二海洋研究所，浙江 杭州 310012；2.南京大學 網絡信息中心，江蘇 南京 210093）

基于標準差準則的海底三維地形模型構建

韓富江1，潘勝玲2，王德剛1，來向華1

（1.國家海洋局第二海洋研究所，浙江 杭州 310012；2.南京大學 網絡信息中心，江蘇 南京 210093）

針對現有三角剖分需要投影到平面，局部優化時屬性丟失的問題，本文采用一種顧及水深屬性的三角剖分準則——標準差準則進行三角剖分，并且討論了標準差的含義、標準差的計算以及標準差準則的描述。根據標準差準則，實現了一種基于標準差準則的海底三維地形模型構建方法。實驗結果表明該方法提高了三角剖分的合理性，模型重建的細節與精確程度更高，在處理特殊地形上優于基于空外接圓準則的TIN模型構建方法。

標準差準則；海底三維地形模型；不規則三角網；特殊地形

虛擬海洋環境仿真是數字海洋建設的重要組成部分，它以數字的方式，逼真地模擬再現海洋環境，使人們可以探索有關海洋的自然和人文信息，并與之互動。而海底三維地形模型的構建是虛擬海洋環境仿真的關鍵技術，對虛擬海洋環境仿真的效果有著重要影響。

海底三維地形模型的構建通常采用數字地面模型（Digital Terrain Model，DTM）。目前，數字地面模型包括3種基本數據結構：等高線結構（Contour）、規則格網結構（Grid）以及不規則三角網結構（Triangulated Irregular Network，TIN）。基于等高線的DTM是由一系列等高線集合和其對應的高程值組成，等高線按有序的坐標點存儲，可認為是帶有高程屬性的簡單多邊形或多邊形弧段[1]。通過等高線和流線（等高線的法線方向）可把地形表面劃分成不規則的多邊形，有利于簡化水文模型的分析計算[2]，因而等高線結構DTM在水文模型等地學分析領域應用較多。規則格網結構DTM計算處理簡單，但不能準確表示地形的結構和細節，在地形平坦的地方，存在大量的數據冗余；在不改變格網大小的情況下，難以表達復雜地形的突變現象[3]。而不規則三角網結構TIN模型由于頂點分布的任意性，能夠較好地反映地形表面特征及變化。TIN模型在表現地形表面起伏特征上具有規則格網無可比擬的優勢。同時，由于TIN模型結構緊湊，在相同表現效果的前提下，TIN模型所需的頂點數目要少于規則格網模型，從而TIN模型的數據量往往要比規則格網模型的數據量要小得多[4]。因此，基于海量數據的海底三維地形模型構建通常采用TIN模型。

TIN模型構建的核心技術就是散點的三角剖分，三角剖分過程也就是TIN的構建過程。而三角剖分準則決定著三角形的幾何形狀和生成TIN模型的質量[5]，影響著模型所表達地形的逼真度和精度。目前常用的三角剖分準則有：最短距離和準則、對角線準則；Lee、Lawson提出的空外接圓準則、最大最小角準則、張角最大準則[6,7]；徐利治提出的面積比準則[8]等。理論上空外接圓準則、最大最小角準則、張角最大準則是等價的，可以保持三角網的唯一性，其余的則不然。對角線準則含有主觀因素，現今已使用不多[5]。這些成果為TIN模型的構建研究提供了重要的借鑒和技術參考。然而這些傳統的準則在進行散點集的三角剖分時，首先依據散點的平面分布確定一個三角網，然后將第三維數據如水深附加于平面三角網上，從而形成了包含連續的三角形面元的地形模型，因此它是一種面向曲面（三角形面元）的地形模型構建技術。面向曲面的模型構建方法，僅考慮了曲面元素的平面幾何形狀，而沒有考慮其在空間的分布情況，當空間三角形與平面的夾角超過一定角度時，往往平面上形狀較好的三角形在空間上其形狀并不一定好，平面上形狀不好的三角形在空間上其形狀并不一定不好；另外一個問題是二維平面上的三角剖分忽略了點的屬性值，導致局部優化過程（Local Optimization Procedure，LOP）中數據點的屬性丟失，造成在特殊地形如陡崖、虎口等處構建的TIN模型與實際地表不相符。

為了解決上述問題，本文采用標準差準則[9]，將散點三維數據（x,y,h）計算得到的標準差，作為判斷三角形形狀在空間上好壞的依據，該準則將水深值引入三角剖分過程，提高了剖分的合理性。同時，在分析總結現有TIN剖分準則和算法的基礎上，實現了一種基于標準差準則的海底三維地形模型構建方法，并實驗證明該方法構建的海底三維地形模型更能反映海底的真實地表。

1 標準差準則

1.1 標準差的含義

標準差是一種量度數據分散程度的標準，用于衡量一組數據對算術平均值的離散程度。標準差較大，表示大部分數據與算術平均值之間的差異較大；標準差較小，表示這些數據較接近算術平均值。在TIN模型的構建過程中，標準差則是衡量一個三角形接近正三角形程度的標準。對于一個三角形而言，三角形的三個頂角角度作為樣本數據，其算術平均值為60°，計算出的標準差越小表示三角形的三個頂角越接近60°，也意味著該三角形越接近正三角形，符合了TIN模型中三角形的幾何形狀盡量接近正三角形的剖分原則。

1.2 標準差的計算

在概率論與數理統計中，離散型隨機變量的標準差計算公式[10]為：

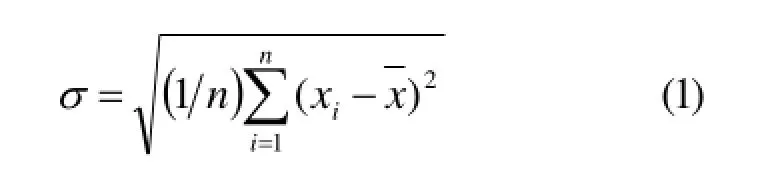
其中n表示隨機變量的個數；為n個隨機變量的算術平均值。對于TIN模型中的一個三角形ABC而言（圖1），假設三個頂點坐標為A（x1，y1，h1），B（x2，y2，h2），C（x3，y3，h3）,三個頂角為A、B、C，其算術平均值為60°,則標準差的計算公式（1）可以改寫為：

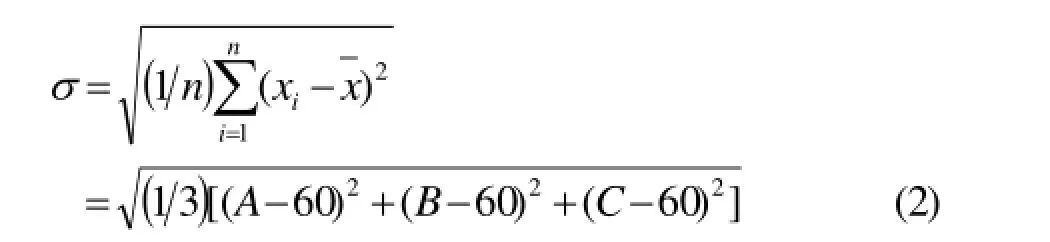
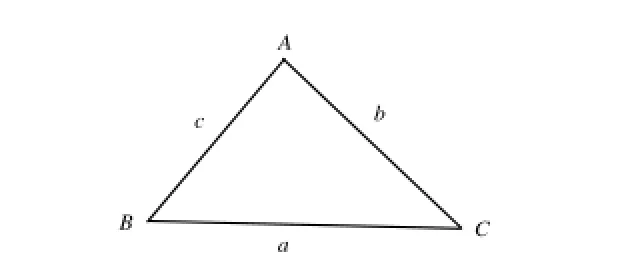
圖 1 三角形示意圖Fig.1 Triangle sketch

式(2)中的A、B、C表示三角形的三個頂角，可由三角形的余弦定理求得：

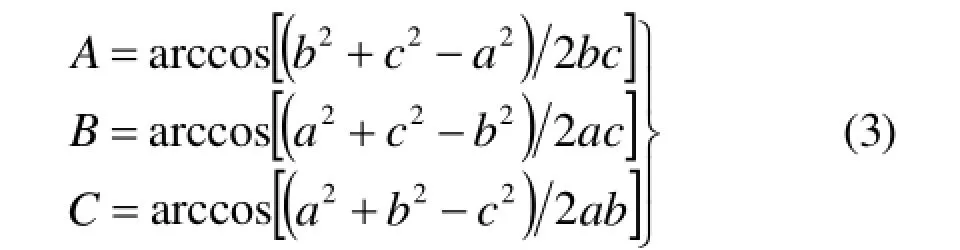
式(3)中的a、b、c表示三角形的三條邊長，可由空間兩點的距離公式求得：

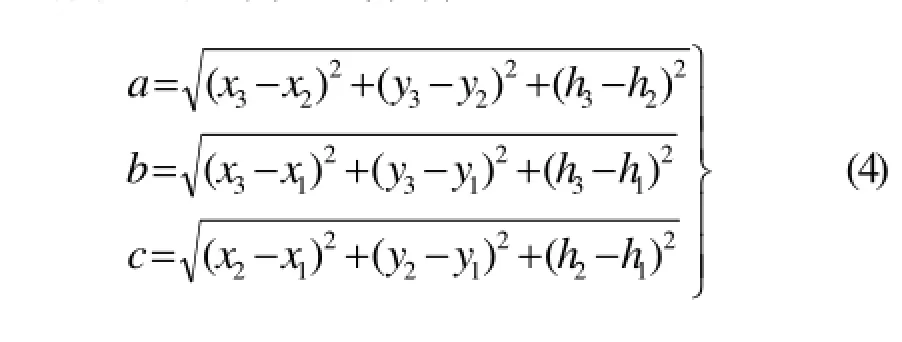
1.3 標準差準則描述

標準差準則就是TIN模型構建中一種三角形的剖分法則，指在兩相鄰三角形形成的凸四邊形中，這兩三角形的標準差之和一定小于交換凸四邊形對角線后所形成的兩三角形的標準差之和。利用標準差準則進行三角形剖分時，原始空間數據的三維坐標（x,y,h）參與三角形形狀好壞的判斷，不需要投影到平面上，直接從空間上進行三角剖分，剖分結果更符合空間實際的地形表面。

標準差準則的基本思想是將空間4點組成的四邊形進行三角剖分劃分為了兩種情形a和b（圖2），分別計算兩種情形下的三角形標準差之和，如果情形a的三角形標準差之和小于情形b的兩個三角形標準差之和，根據TIN模型中三角形的幾何形狀盡量接近正三角形的原則，選擇情形a作為構建TIN的三角形，否則，選擇情形b。

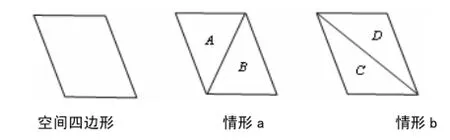
圖 2 標準差準則Fig.2 Standard deviation criterion

對情形a和情形b中的三角形A、B、C、D以其內角的角度作為樣本數據，根據公式(2)分別計算其標準差，用σA、σB、σC、σD表示。則情形a中A、B兩個三角形的標準差之和為σA+σB；情形b中C、D兩個三角形的標準差之和為σC+σD。根據標準差準則，可以通過判斷σA+σB與σC+σD的大小，選擇情形a還是情形b作為構建TIN模型的優化三角形。如果（σA+σB）－（σC+σD）小于零，則情形a好；（σA+σB）－（σC+σD）大于零，則情形b好；（σA+σB）－（σC+σD）等于零，則兩種情形一樣好，選擇情形a或是情形b都可以。

2 基于標準差準則的海底三維地形模型構建

一個良好的數據結構和三角形剖分準則，必須有高效的算法和程序實現。目前離散型數據集的TIN模型構建使用最為廣泛的是Delaunay直接三角剖分算法，包括分割合并算法、三角網增長算法和逐點插入算法[5]。由于分割合并算法是遞歸執行，內存開銷較大；三角網增長算法最大的問題是計算的時間復雜性，數據點越多問題越突出[11]；而逐點插入算法在很大程度上克服了上述問題，并且概念簡單，容易實現，還能夠進行約束三角剖分，所以本文構建海底三維地形模型的方法沿用了逐點插入法的基本思想，只是把LOP時采用的空外接圓準則替換為標準差準則，在空間上直接對散點進行剖分，提高模型重建的細節與精確度。

算法的基本思想是：先在包含所有數據點的多邊形中建立初始三角網，然后在已存在的三角網中插入數據點，找到包含該數據點的三角形，連接該點與其所在三角形的三個頂點形成新的三個三角形，用標準差準則優化新形成的三角形，直至所有數據點都插入到三角網中。具體的算法步驟如下：

步驟1 建立包含所有數據點的初始包容盒，該包容盒可以為凸殼、矩形包容盒或超級三角形，并對該包容盒進行初始三角剖分。本文選用的包容盒為超級三角形，超級三角形的三個頂點坐標可以通過以下方法得到。假設離散數據集中含有n個離散點，坐標為（xi，yi，hi），i=1,2,…,n。對離散點的坐標進行比較得到最大值xmax，ymax，最小值xmin，ymin，hi為水深值。通過以下公式計算得到坐標范圍dx，dy，坐標范圍最大值dmax以及坐標中間值xmid，ymid。

步驟2 往初始三角網中插入數據點，設當前處理數據點為P，首先找出包含點P的三角形T，設T的三頂點為V1、V2、V3，然后P與T三頂點相連，形成三個新的三角形T1、T2、T3，如圖3所示。

步驟3 對所有新形成的三角形，利用標準差準則進行優化處理。為了對所形成的新三角形進行優化，需要將包含當前點的三角形的相鄰三角形放入一個堆棧中。然后從堆棧中每次彈出一個三角形，與包含插入點的三角形進行LOP優化，如果進行了對角線交換，相鄰三角形也要放入堆棧，這是一個循環過程，直到堆棧為空，方可進行下一點的處理。具體優化過程如下：

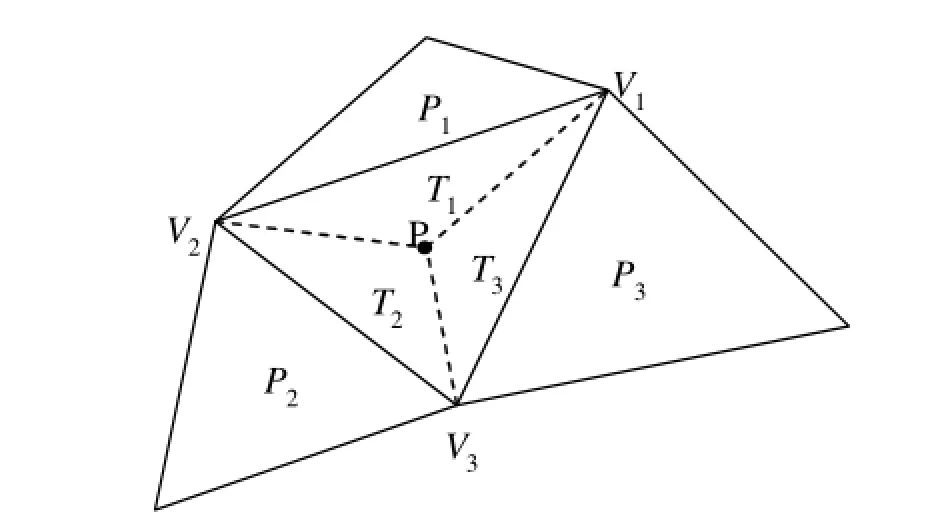
圖 3 包含點P的三角形及初始三角剖分Fig.3 Triangle including point P and initial triangulation

（1）把包含P的三角形的三個鄰接三角形P1、P2、P3放入堆棧中；

（2）從堆棧中彈出三角形P3；

（3）計算三角形P3與鄰接三角形T3的標準差之和σ1，以及交換對角線之后兩個三角形的標準差之和σ2。如果σ1大于σ2，則需要交換對角線，否則，彈出下一個三角形；

（4）如果交換對角線，原來與P3相鄰的兩個三角形也要壓入堆棧；

（5）重復（2）－（4），直到堆棧為空，則P點的插入過程結束。

步驟4 重復步驟（2）－（3），直至所有數據點都被插入到TIN模型中。

步驟5 處理外圍三角形，完成海底三維地形模型的構建。由于超級三角形的頂點并不是水深離散點集中的點，所以要將包含超級三角形頂點的三角形和超級三角形的三個頂點移除，得到最終的海底三維地形TIN模型。

基于標準差準則的海底三維地形模型構建方法較好地解決了LOP時水深屬性丟失的問題，同時，對數據點的三角剖分直接在空間進行，提高了海底地形TIN模型的細節性和準確性。

3 實驗與分析

為了驗證基于標準差準則海底三維地形模型構建方法的優越性，本文在C#.NET開發環境中編程實現了該方法，構建了海底三維地形TIN模型，并且與利用空外接圓準則構建的海底三維地形模型進行了對比分析。實驗選取的數據為由SeaBeam 2112多波束測深系統測得的水深數據，共有5 844個數據點，數據分布比較均勻，數據點的三維顯示如圖4所示。由圖4可以看出本文所選實驗區的海底地形起伏變化較大，并且還有一個特殊地形陡崖。

圖4 水深數據點的三維顯示Fig.4 Three-dimensional display of bathymetric data points

基于標準差準則算法構建的海底三維地形TIN模型如圖5（a）所示；空外接圓準則算法構建的海底三維地形TIN模型如圖5（b）所示。

由圖5（a）可以看出，基于標準差準則算法構建的海底三維地形TIN模型有效地避免了狹長三角形的出現，保證了三角形形狀在空間上的良好性，解決了水深屬性丟失的問題，使得在特殊地形陡崖處構建的TIN更接近海底的真實地表。而空外接圓準則算法構建的海底三維地形模型，由于其三角剖分過程是在投影平面上進行，造成陡崖處的TIN很凌亂，狹長三角形較多，不符合三角剖分的原則，也不能反映特殊地形的真實表面，結果如圖5（b）所示。兩種方法構建的海底三維地形模型不一致的主要原因是在利用空外接圓準則對TIN模型進行優化的過程中，只用到了數據點的（x,y）坐標，沒有顧及水深屬性，并且需要投影到平面xoy上進行，這樣就造成在空間上形狀較好的三角形，投影到平面上反而變成了狹長三角形；空間上狹長的三角形，投影到平面上反而接近正三角形。特別是在陡崖等特殊地形，上部的數據點投影到平面上還有可能與下部數據點重合或相鄰較近，在三角剖分過程中，容易引起狹長三角形的形成。基于標準差準則的算法則直接在空間對水深數據點進行三角剖分，利用數據點三維坐標（x,y,h）計算得到的標準差作為判斷三角形形狀好壞的依據，剖分準則顧及了海底地形的屬性水深值，提高了海底地形三維TIN模型的細節性和準確性。

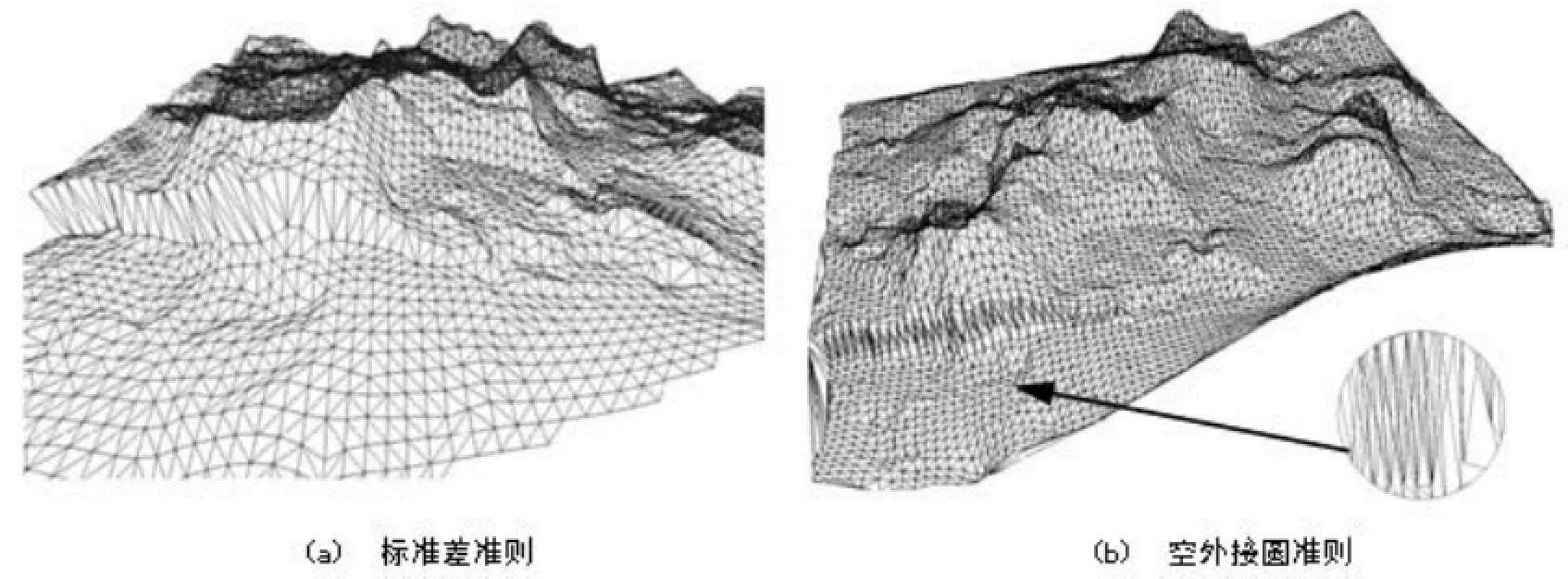
圖5 兩種剖分準則構建的海底三維地形模型透視圖對比Fig.5 Contrast of three-dimensional seabed terrain model constructed by different algorithms

4 結 語

本文在分析現有三角剖分準則的基礎上，采用一種顧及水深屬性的三角剖分準則—標準差準則進行三角剖分，該準則克服了原有剖分準則需要投影到平面上進行三角剖分的不足，解決了LOP時屬性丟失的問題。根據標準差準則，實現了一種基于標準差準則的海底三維地形模型構建方法。實驗結果表明該方法提高了三角剖分的合理性，模型重建的細節與精確程度更高，在處理特殊地形上優于基于空外接圓準則的TIN模型構建方法。由于水深測量數據的海量性，基于標準差準則的海底三維地形模型的構建效率以及模型的紋理映射處理都需要進一步的深入研究。

[1]Moore I D, Grayson R B.Terrain-based Catchment Partitioning and Runoff Prediction Using Vector Elevation Data [J].Water Resources Research.1991b, 27(6):1177-1191.

[2]Wilson J P, Gallant J C.Terrain Analysis: Principles and Applications [M].New York: John Wiley and Sons, 2000.

[3]鄔倫, 劉瑜, 張晶, 等.地理信息系統-原理、方法和應用 [M].北京: 科學出版社, 2001.

[4]石松.虛擬地理環境中地形建模及其空間分析研究 [D].福州:福州大學, 2005.

[5]湯國安, 劉學軍, 閭國年.數字高程模型及地學分析的原理與方法 [M].北京: 科學出版社, 2005.

[6]Lee D T, Schachter B J.Two Algorithms for Constructing a Delaunay Triangulation [J].Int.Journal of Computer and Information science.1980, 9(3): 219-242.

[7]Lawson C L.Software for c' Surface Interpolation [C]//Mathematical Software III, New York: Academic Press, 1977: 161-194.

[8]徐利治.逼近論 [M].北京: 國防工業版社, 1985.

[9]潘勝玲, 劉學軍.基于標準差的地形三維表面模型建立方法 [J].計算機應用研究, 2007, 24(11): 295-297.

[10]余錦華, 石北源, 楊維權.概率論與數理統計[M].廣州: 中山大學出版社, 2000.

[11]李志林, 朱慶.數字高程模型 [M].武漢: 武漢大學出版社, 2003.

Construction of 3D Seabed Terrain Model based on the Standard Deviation Criterion

HAN Fu-jiang1, PAN Sheng-ling2, WANG De-gang1, LAI Xiang-hua1

(1.Second Institute of Oceanography, SOA, Hangzhou 310012, China; 2.Network Information Center, Nanjing University, Nanjing 210093, China)

At present, existing triangulation must be done in the projection plane, so it causes the loss of attribution information in LOP (Local Optimization Procedure).In this paper, a new triangulation criterion based on standard deviation is used.The definition of standard deviation, calculation of standard deviation, and description of standard deviation criterion is investigated.Then the construction algorithm of 3D seabed terrain model based on standard deviation is presented according to the standard deviation criterion.The result of experiment shows that this method improves the rationality of triangulation, the details and precision of seabed terrain model are better than others, and it is better in dealing with special terrain than the algorithm based on empty circum-circle criterion.

standard deviation criterion; three-dimensional seabed terrain model; Triangulated Irregular Network; special terrain

TP311

A

1001-6932(2011)06-0674-05

2011-01-05；

2011-05-23

國家海洋局第二海洋研究所基本科研業務費專項資金資助項目（JG0913, JT0803, JG0911）。

韓富江（1977－），男，碩士，工程師，主要從事三維建模及可視化、海洋測繪、DEM及地形分析方面的研究。電子郵箱: hfj111@126.com。