微分方程系統不可積性問題研究

焦 佳，高 洋，周慶健

(大連民族學院理學院，遼寧大連 116605)

微分方程系統不可積性問題研究

焦 佳，高 洋，周慶健

(大連民族學院理學院，遼寧大連 116605)

研究了周期系統Laurent多項式型首次積分和有理首次積分的不存在性問題。利用Floquet理論，證明了如果系統的特征乘數是? －非共振的，則系統在平衡點附近不存在Laurent多項式型首次積分。進一步，還在有理函數空間考慮了這一問題，并得到了相應的結果。

Floquet理論;Laurent多項式型首次積分;形式首次積分;有理首次積分

1 自治系統

在物理、力學、化學、生物、工程等領域的各種動態數學模型，往往歸結為非線性微分方程。這些方程可分為兩大類:可積的與不可積的。一般說來，隨著時間的變化，可積系統總是呈現出有規律的可預測的行為;而在很多情況下，不可積系統在其相空間的某區域上的運動是無規律的和混沌的。長期以來，由于解方程的需要，可積性問題已變成數學和物理學家所關心的基本問題之一，并得到了很多重要的結果。近些年來，隨著人們對混沌現象越來越感興趣，對不可積系統的研究也越來越多。

考慮如下解析系統

式中，x=(x1，…，xn)∈?n，f(x)=(f1(x)，…，fn(x))。

定義1 單值函數Φ(x)稱為系統(1)的一個首次積分，如果Φ(x)沿著系統(1)的任何一條解曲線都是常數。若Φ(x)是可微的，則可將其寫為

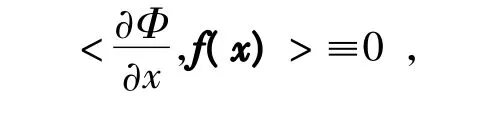
式中，＜.，.＞表示歐式空間的內積。

對于給定的系統(1)，在什么樣的條件下系統具有首次積分?除了某些簡單的情形，這個問題是非常困難的，并且迄今尚無一種辦法能對一給定的系統構造出首次積分，因此證明系統的可積性是非常困難的。這樣，迫使人們不得不換一個角度來證明系統的不可積性，即:如果系統(1)(在某個函數空間)不存在任何首次積分，則稱系統(1)(在此函數空間上)是不可積的。

注1detA≠0，這個條件是可以去掉的。因為事實上，不滿足共振條件(3)已經保證了這個條件。

定義2設K是給定的數域，αi∈K，{b1，…，bk}是復向量空間E的一個有限子集，如果α1b1+α2b2+… +αkbk=0蘊含 α1=α2=… =αk=0，則稱b1，…，bk是K －獨立的。

近年來，眾多學者都開始關注這方面的問題，先后在解析函數、有理函數、多項式和Laurent多項式等函數空間，對一般非線性系統、擬齊次系統和半擬齊次系統給出了不存在首次積分的判別準則。

1983 年，Yoshida［2］利用奇性分析法，根據Kovalevskaya指數［3］(以下簡稱 K － 指數)給出了一類尺度不變系統代數可積的必要條件。

定理2如果系統(1)是弱代數可積的，那么所有K－指數都是有理的。

這個結果雖然在當時被人們廣泛地應用，但是在1991 年，Kummercite［4］對于這個定理給出了一個反例。進而，人們對這個定理進行了修正，得到了如下修正后的Yoshida定理［2］。

定理3如果系統(1)是代數可積的，那么所有K－指數都是有理的。也就是說，如果至少有一個K－指數是無理數或虛數，那么系統不是代數可積的。

隨后，人們在不同的函數空間也考慮了這個結果［5－6］。

定理4如果存在一個平衡ξ使K－矩陣是半單的，且K－指數 ρ1，…，ρn是? －獨立的(? －

那么系統(1)沒有任何非平凡的多項式首次積分。進一步，如果系統(1)是正半擬齊次的，那么在x=0附近不存在任何非平凡的形式首次積分。

1996 年，Nowicki［8］利用微分代數理論，對線性系統

給出了存在形式首次積分和有理首次積分的必要條件。

定理6設線性系統(2)的矩陣A是半單的。如果特征值λ1，…，λn是? －獨立的，那么當且僅當系統(2)沒有任何非平凡的形式首次積分。另外，如果特征值是獨立的，那么當且僅當系統(2)沒有任何非平凡的有理首次積分。

注2這里稱矩陣A半單是指矩陣A是可對角化的。

2003年以來，史少云先后給出了一般非線性系統和半擬齊次系統不存在Laurent多項式首次積分和有理首次積分的判定準則，見文獻［9－10］。

例1 考慮如下廣義的二維Volterra－Lotka系統第一種判別法:

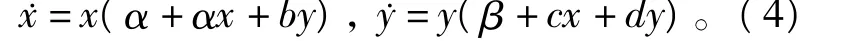
由定理1可知，如果對任意k1，k2∈?∪{0}，k1+k2≥1，獨立的)，那么不存在有理(多項式)首次積分。

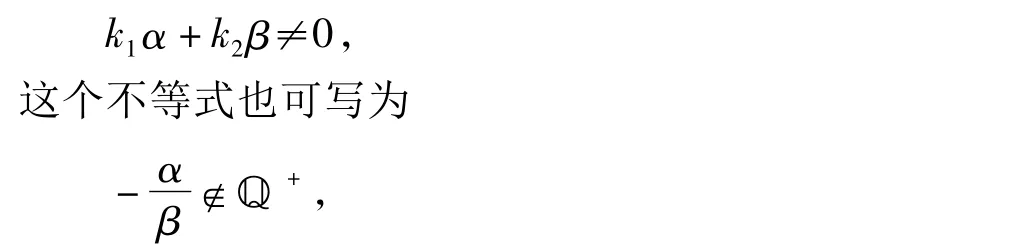
受到 Yoshida 工作的啟發，1996 年，Furta［7］研究了半擬齊次系統的不可積性，利用K－指數給出了半擬齊次系統不存在解析首次積分的判定準則。

定理5設系統(1)是半擬齊次系統，如果其擬齊次截斷系統的K－矩陣是對角的，且它的特征值λ1，…，λn不滿足任何共振等式

那么系統(4)在x=y=0附近沒有任何非平凡的解析首次積分。

第二種判別法:

系統(4)是負半擬齊次系統，在指數sx=sy=1下有二階擬齊次截斷，

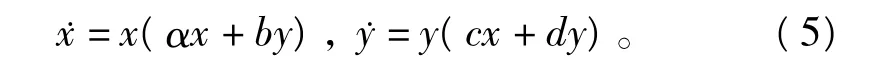
如果ad－bc≠0，則系統(5)有如下形式的特解:根據定理5，如果

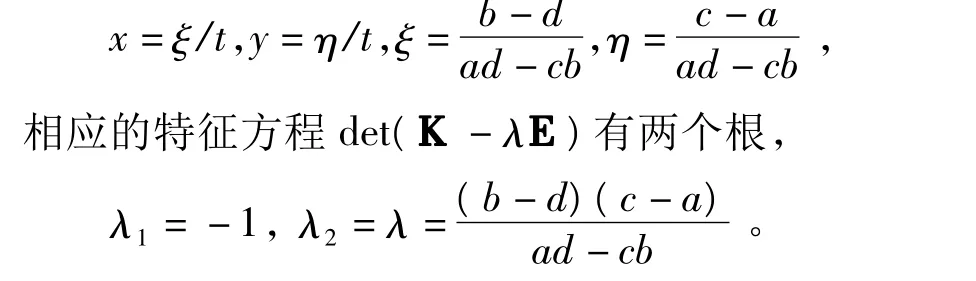
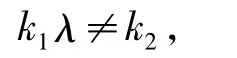
那么系統(4)沒有非平凡的多項式首次積分。此不等式還可寫為

2 非自治周期系統

考慮如下周期系統

其中(t，y)∈S1× ?n(S1= ? /? T)，且f(t+T，y)=f(t，y)。設y=0是系統的平衡點，即對所有的 t∈S1都有f(t，0)=0。可將系統(6)重寫為

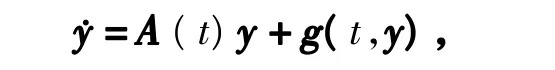
式中，A(t+T)=A(t)，g(t，y)是關于y 的展開式中所有高于一次的項的總和，且滿足g(t+T，y)=g(t，y)。

定義3 稱單值函數Φ(t，y)為周期系統(6)的首次積分，若Φ(t，y)關于t是T－周期函數且沿著系統(6)的任何一條解曲線都是常數。如果Φ(t，y)是可微的，則可將其寫為

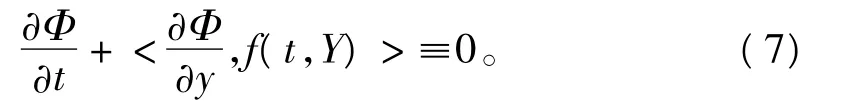
如果Φ(t，y)可展開成關于y的形式冪級數(有理函數)且滿足式(7)，那么稱 Φ(t，y)系統(6)的形式(有理)首次積分。

注3 我們還考慮了系統(6)的Laurent多項式型首次積分，這里，Laurent多項式是指

式中，Φk1，…，kn(t)是關于 t的函數，A 是整數集?n的一個有限子集。如果Φ(t，y)關于t是T－周期的可微函數，且滿足式(7)，那么稱函數Φ(t，y)是系統(6)的Laurent多項式型首次積分。

根據定義，常值函數顯然是系統(6)的首次積分，稱為平凡積分。本文中所說積分都是指非平凡的。

那么系統(6)在y=0附近不存在任何非平凡的形式首次積分。

我們主要給出了這個定理的一個新的證明［13］且考慮了系統(6)Laurent多項式型首次積分的不存在性［14］，并進一步在有理函數空間考慮了此結果［15］，得到如下定理:

定理8設y=0是系統(6)的平衡點，若系統(6)的特征乘數是? －非共振的，即不滿足任何共振條件

由Floquet理論［11］知，存在周期為 T的矩陣函數B(t)，使得在線性變換

下，系統(6)變為

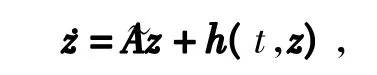
式中，~A是一個常數矩陣;h(t，z)是關于z的展開式中所有高于一次的項的總和，且滿足h(t+T，z)=h(t，z)。矩陣~A的特征值λi稱為系統

的特征函數，矩陣eT~A的特征值μi=eλiT稱為式(8)的特征乘數。

2003年，李偉顧等人［12］研究了微分同胚和如上周期系統(6)形式首次積分的不存在性。

定理7設y=0是系統(6)的平衡點，如果系統(8)的特征乘數不滿足任何共振條件:

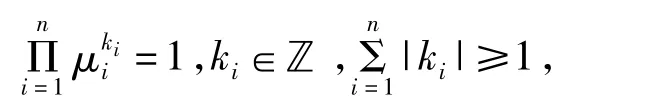
那么系統(6)在平衡點附近沒有任何非平凡的Laurent多項式型首次積分。

定理9設y=0是系統(6)的平衡點，且μ1，…，μn是線性系統(8)的特征乘數，如果系統(6)在平衡點y=0附近有一個非平凡有理首次積分，則存在非零整數向量k=(k1，…，kn)∈?n使得的基本解矩陣為

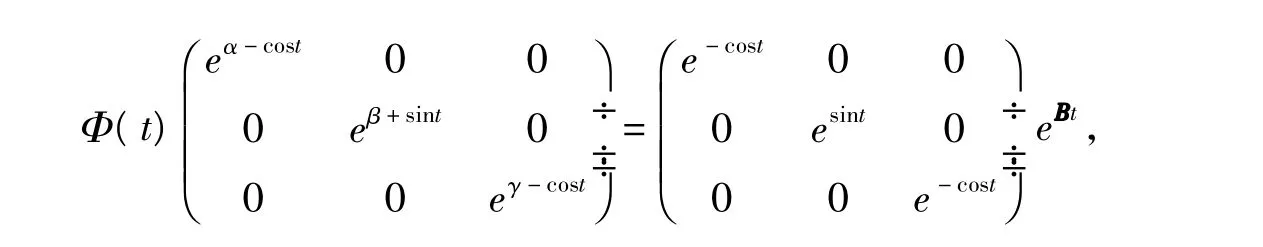
根據定理9，周期系統(9)在平衡點附近沒有任何非平凡的有理首次積分。

3 結語

介紹了解析系統不可積性的一些判定準則。針對已有結果大多考慮的是自治系統，而對于非自治的周期系統研究的還很少，這里給出了非自治周期系統不存在Laurent多項式型首次積分和有理首次積分的充分條件。

［1］ POINCARé H. SurI ＇intégrationsdes équations fifférentielles du premier order et dupremier degré I and II Rend［J］.Circolo Mat Palermo，1891，11:193 －239.

［2］YOSHIDA H.Necessary condition for the non － existence of algebraic first integral(Ⅰ，Ⅱ) ［J］.Celestial Mech，1983，31:363－379，381－399.

［3］KOWALEVSKI S.Sur le probleme de la rotation d＇un corps solide autour d＇un point fixe ［J］.Acta Math.，1889，12:177－232.

［4］KUMMER M，CHURCHILL R C，ROD D L.On Kovalevski expoenents［J］.Can.Math.Bull.，1990，33:175－180.

［5］ GORIELY A.Integrability，partial integrability，and nonintegrability for systems of ordinary differential equations［J］.J.Math.Phys.，1996，37:1871 －1993.

［6］SADETOV S T.On resonances of the Kovalevskaya exponents［J］.Math.Notes，1993，54:1081 －1083.

［7］FURTA S D.On non－integrability of general systems of differential equations［J］.Z Angew Math Phys，1996，47:112－31.

［8］NOWICKI A.On the nonexistence of rational first integrals for systems of linear differential equations［J］.Linear Algebra Appl，1996，235:107 －120.

［9］SHI Shaoyun，LI Yong.Non－integrability for general nonlinear systems［J］.Z Angew Math Phys，2001，52:191－200.

［10］SHI Shaoyun.On the nonexistence of rational first integrals for nonlinear systems and semiquasihomogeneous systems［J］.J.Math.Anal.Appl.，2007，335:125－134.

［11］CHICONE C C.Ordinary Differential Equationas with Applications［M］.New York:Springer－ Verlag，1999.

［12］LI Weigu，LLIBRE J，ZHANG Xiang.Local first integrals of differential systems and diffeomorphisms［J］.Z Angew Math Phys，2003，54:235 －255.

［13］JIAO Jia，SHI Shaoyun，XU Zhiguo.Formal first integrals for periodic systems［J］.J.Math.Anal.Appl.，2010，366:128－136.

［14］焦佳，付苗苗，馬勇.周期系統Laurent多項式型首次積分的不存在性［J］.吉林大學學報:理學版，2009，47:44－47.

［15］JIAO Jia，SHI Shaoyun，ZHOU Qingjian.Rational first integrals for periodic systems［J］.Z Angew Math Phys，2011，62:233 －243.

Non－integrability of Differential Equation Systems

JIAO Jia，GAO Yang，ZHOU Qing－jian

(College of Science，Dalian Nationalities University，Dalian Liaoning 116605，China)

The nonexistence of the first integrals of Laurent polynomial and the rational first integrals for periodic systems are considered.Using the Floquet theory，that if the characteristic multipliers of the system are ? － dependent，then the system does not have any nontrivial integral of Laurent polynomial in a neighborhood of a constant solution is proved.Furthermore，the previous conclusion in the rational function space is also considered.

Floquet theory;Laurent polynomial first integral;formal first integral;rational first integral

O175

A

1009－315X(2011)05－0472－04

2011－05－25;最后

2011－06－16

國家自然科學基金資助項目(10872045);大連民族學院博士啟動基金資助項目(20096209)。

焦佳(1982－)，女，河南焦作人，講師，博士，主要從事非線性常微分方程研究。

(責任編輯 鄒永紅)