圖書借閱預測的ARIMA乘積季節模型構建及實證分析①

劉 琳

(華北科技學院圖書館，北京東燕郊 101601)

圖書借閱預測的ARIMA乘積季節模型構建及實證分析①

劉 琳②

(華北科技學院圖書館，北京東燕郊 101601)

本文研究乘積季節模型在我校圖書借閱預測中的應用，通過對我校2007年1月到2009年12月的月度圖書借閱數據來進行實證分析，采用差分方法對序列資料進行平穩化，然后進行模型定階并估計其參數，建立了我校圖書借閱的乘積季節預測模型ARIMA(4，1，1)(1，1，1)12。對模型進行診斷檢驗，結果表明，用該乘積季節模型對我校的圖書借閱擬合效果較好。最后，利用此模型對我校2010年1至6月進行了預測，與實踐有較好的擬合。

乘積季節模型;時間序列分析;圖書借閱量;預測

0 引言

圖書館作為高校的第二課堂，主要滿足在校教師和學生的學習研究的資料查詢及借閱需求。圖書借閱預測和分析對圖書資料的管理和用戶行為的調節等都具有十分積極的意義。

目前國內對圖書借閱預測比較活躍，但建模研究基本上是季節性AR模型。本文探討了采用乘積季節型模型，對我校圖書借閱的預測結果表明，該模型具有較好的擬合效果。

1 乘積季節模型

1.1 乘積季節模型簡介

時間序列分析是一種根據動態數據揭示系統動態規律的統計方法，其基本思想是根據系統的有限長度的運行記錄，建立能夠比較精確地反映時間序列中所包含的動態依存關系的數學模型，并借此模型對未來行為進行預測。

ARIMA模型屬于隨機時間序列分析方法。隨機序列分為平穩序列(統計特征不隨時間變化)和非平穩序列(不具有平穩性)，對于平穩時間序列可以建立自回歸模型(AR(p))、移動平均模型(MA(q))和自回歸移動平均模型(ARMA(p，q))。非平穩的時間序列可以先進行d階差分運算，然后建立 ARMA模型，即 ARIMA(p，d，q)模型。乘積季節模型是隨機季節模型與ARIMA模型的結合。

包含季節性的時間序列也不能直接建立ARMA模型，須進行季節差分消除序列的季節性，差分步長與季節周期一致，一般地，如果序列經過D

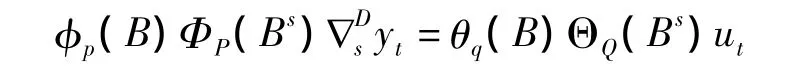
式中，p是季節自回歸階數，q是季節移動平均階數，并且分別Φp(Bs)和ΘQ(Bs)季節P階自回歸算子和Q階移動平均算子。

1.2 乘積季節模型的建模步驟

建立乘積季節模型可歸納為3個具體步驟:數據的平穩化;模型的識別、定階與模型參數估計;模型的診斷檢驗。

1.2.1 數據的平穩化

一般對非平穩數據通過差分或取對數等方式可以將其平穩化。

1.2.2 模型的識別與定階

對乘積季節模型的階數識別及參數估計，基本上采用Box-Jenkins方法，也就是立足于考察數據的自相關和偏自相關分析圖，季節長度s可以由實際應用背景分析得到。

1.2.3 診斷檢驗

模型是否合適，需要對其進行擬合優度檢驗，典型的方法是對殘差序列進行分析，如果殘差序列不是白噪聲序列，則說明還有信息包含在相關的殘差序列中未提取出來，必須修改模型，直到殘差序列是白噪聲序列為止。階周期長度為s的差分，季節性基本消除，如果在季節差分之前還進行了d階逐期差分才平穩，則可以對原序列建立乘積季節模型ARIMA(p，d，q)(P，D，Q)s，記為

2 實證分析

2.1 樣本選取

本文選取的數據為華北科技學院圖書館2007年1月到2010年6月的圖書借閱數據(數據來源于圖書館管理信息系統統計的結果)，我們處理的數據為2007年1月到2009年12月，2010年的數據作為預測數據。

將借閱量的原始數據繪成折線圖，如圖1所示，序列是具有明顯的增長趨勢的非平穩序列，并包含周期為12個月的季節波動。

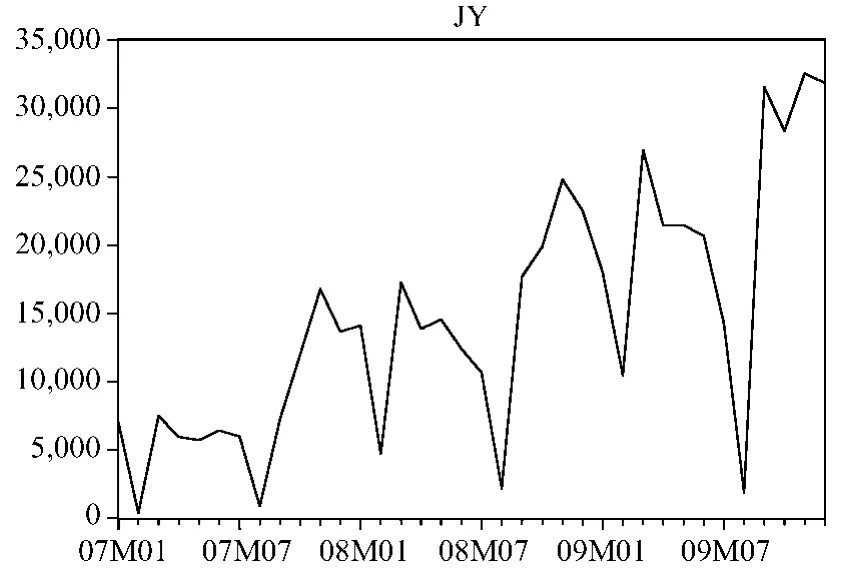
圖1 圖書借閱量折線圖

2.2 數據處理

為消除趨勢同時減少序列的波動，對原序列做一階自然對數逐期差分，得新序列，記為sjyl，即sjyl=log(jyl)-log(jy(-1))。

根據序列sjyl的自相關和偏相關分析圖可以看出序列趨勢基本消除了，但k=12時，樣本的自相關和偏相關系數顯著不為0，表明季節性存在。對序列sjyl做季節差分，記為ssjyl，即

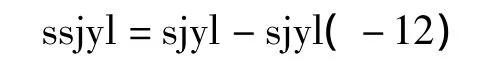
ssjyl的自相關和偏相關分析圖如圖2所示。

從序列ssjyl的自相關與偏相關分析圖可見，序列趨勢和季節性已基本消除，進一步檢驗序列均值為0的假設可接受。

為了進一步檢驗序列是否平穩，對進行單位根檢驗，單位根檢驗是平穩性檢驗的正式方法。

從表1可看出，p檢驗值小于給定的顯著性水平，拒絕原假設，認為序列不存在單位根，是平穩的。表明對序列ssjyl可以直接建立ARMIA模型了。

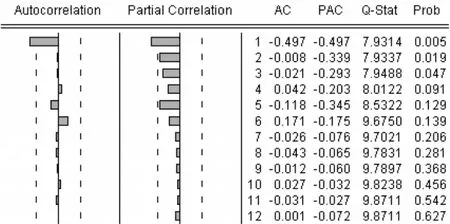
圖2 序列ssjyl的自相關與偏相關分析圖

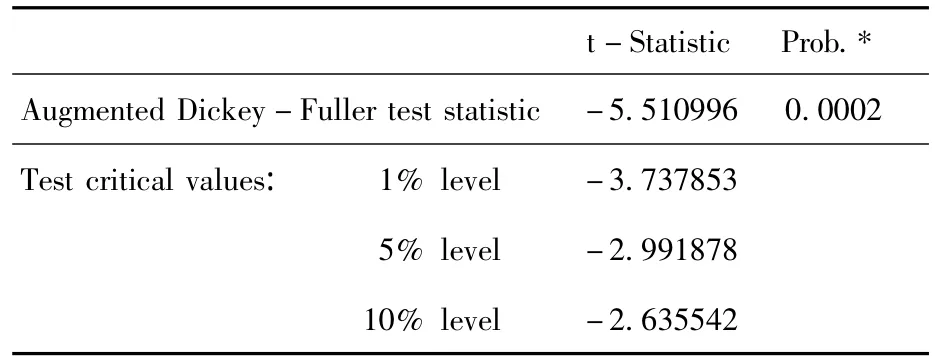
表1 ssjyl序列的單位根檢驗

2.3 模型識別

因為經過一階逐期差分，序列趨勢已基本消除，故d=1;經過一階季節差分，季節性基本消除，故 D=1。所以選用 ARMIA(p，d，q)(P，D，Q)s模型。觀察序列ssjyl的自相關與偏相關分析圖，q=1，p=2或p=3比較合適，考慮到AR模型是線性方程估計，相對于MA和ARMA模型的非線性估計容易，且參數意義便于解釋，故在實際建模中一般希望用高階的AR模型替代相應的MA或ARMA。綜合考慮，可以選擇的(p，q)組合可以有:(3，1)，(4，0)，(4，1)。由于 k=12 時，樣本的自相關與偏相關系數都顯著不為0，所以，P=Q=1。

2.4 模型的建立

利用計量經濟軟件Eviews6.0，可以直接建立模型，求解參數系數，如建立 ARIMA(4，1，1)(1，1，1)12模型。在主菜單選擇Quick/Estimate Equa-tion，打開方程定義對話框，輸入

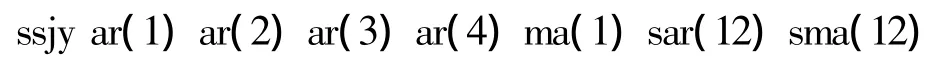
其中，sar(s)和sma(s)分別表示季節自回歸部分和季節移動平均部分的變量。

點擊確定后，得到圖3所示的結果。

2.5 模型選擇與檢驗

將三個模型的參數估計和相關檢驗結果匯總列入表1。

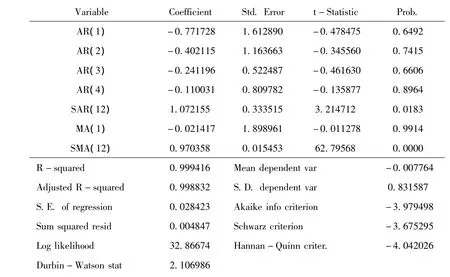
圖3 模型參數估計與相關檢驗結果

表2 各模型參數估計結果及檢驗結果

經計算，各模型都滿足ARMA過程的平穩條件及可逆條件，模型設定都合理，擬合效果較好，其中第3個模型的AIC值最小，因此最終選擇第三個即 ARIMA(4，1，1)(1，1，1)12模型比較合適。

模型診斷通過殘差序列檢驗來實現，如果殘差序列是白噪聲序列，則說明模型是適應的，否則模型需要改進。對以上乘積季節模型進行殘差分析，殘差序列單位根檢驗結果如表2，殘差序列自相關和偏相關分析圖結果如圖4。

表3 殘差序列的單位根檢驗

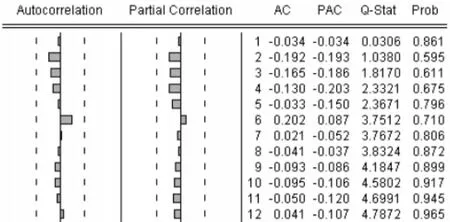
圖4 殘差序列的的自相關與偏相關分析圖

殘差分析表明，殘差序列是平穩的白噪聲，所建立的模型較好地擬合了時間序列的數據變化趨勢。

2.6 預測

利用 ARIMA(4，1，1)(1，1，1)12模型，對我校2009年1月到2010年6月份的借閱量進行了預測，預測結果表3所示。

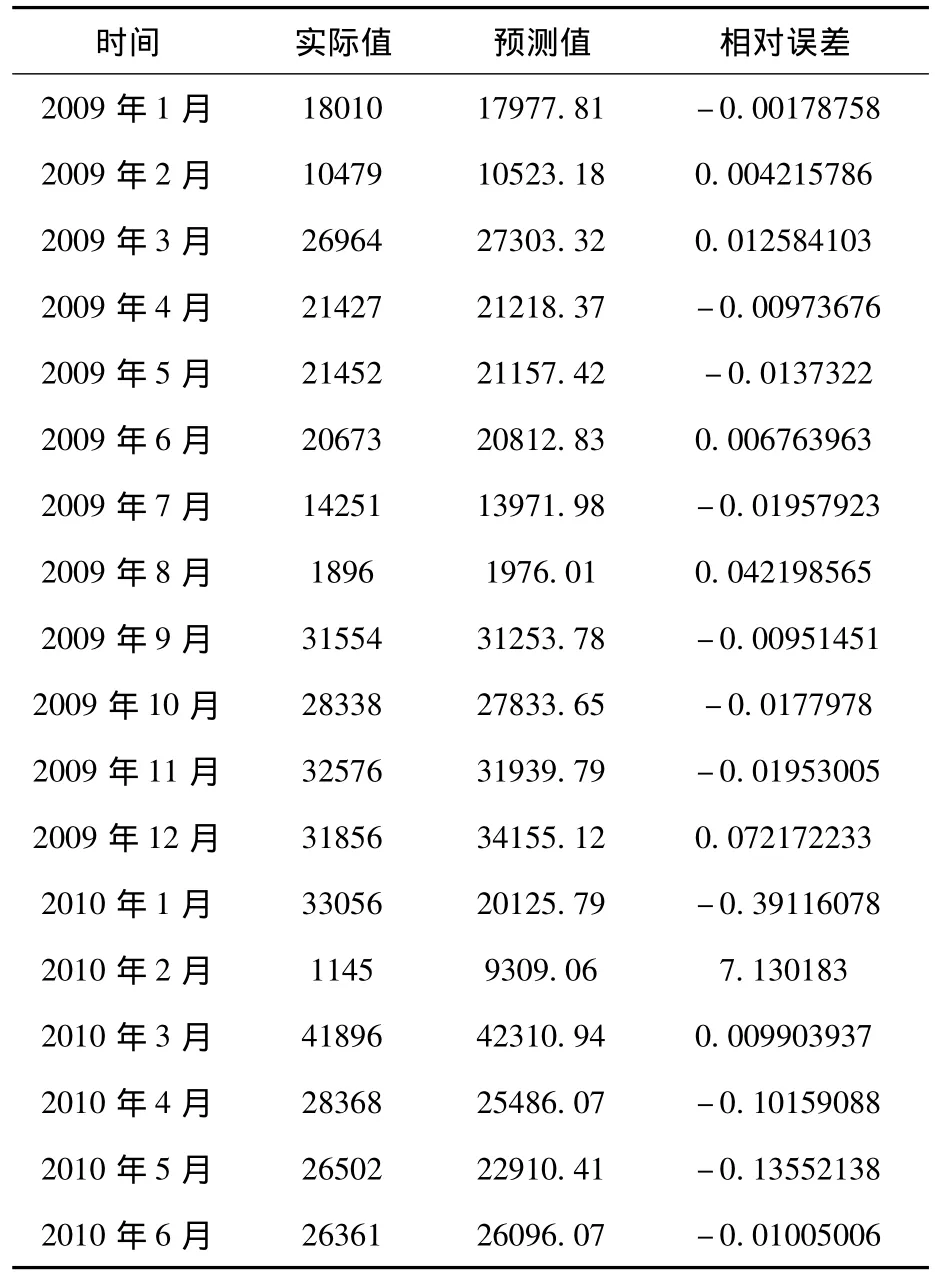
表4 實際值與預測值對比表

從預測結果可以看出，對2009的年數據預測效果非常精確，對2010年的數據除1月份2月份外，也比較精確，這2個月的數據出現大的偏差是因為2010年學校放寒假比往年提前了許多，開學又較晚，2月份學生基本上不在學校，從而導致了1月份的數據突然變大，2月份的數據突然很小，這是往年從來沒有的現象，從而可以看做異常數據，不予理睬。除了這2個月異常外，其他4個月預測結果都非常的滿意，精度很高，我們建立的乘積季節模型是比較理想的。從這里我們可以發現，利用此模型還可以發現異常數據，結合實際情況對異常情況作出合理解釋。

3 結論

與一般時間序列模型相比，乘積季節模型需要更多的歷史數據，相對于其他時序模型，乘積季節模型具有更廣泛的適用范圍，在現實的經濟生活中具有明顯的趨勢和季節性特點的數據非常普遍，因此乘積季節模型較好地解決了這類問題的預測問題，精度較高。本文所建立ARIMA(4，1，1)(1，1，1)12模型較好地擬合了我校圖書借閱規律，而且歷史數據越豐富，模型預測的結果越精確，本文所介紹的乘積季節模型方法具有較好的實用性。

［1］ 易丹輝.數據分析與Eviews應用［M］.北京:中國人民大學出版社，2009

［2］ 彭志行等.ARIMA乘積模型及其在傳染病發病預測中的應用［J］.數理統計與管理，2008，(3):75～79

［3］ 張歡.中國煤炭價格的ARIMA模型的建立及其預測分析［J］.廣西師范大學學報(自然科學版)，2006，(2):9 ～13

Application of ARIMA multiplicative Seasonal Model to the Forecast for Books Borrowing

LIU Lin

(The library of North China Institute of Science and Technology，Yanjiao Beijing-East 101601)

This article mainly researched the application of multiplicative seasonal model to the forecast forHuake’s books borrowing.It empirically analyzed the number of books borrowing to our university from January 2007 to June 2010.applied difference method to stabilize the sequence data，then made order determination and parameter estimation for the model，established the multiplicative seasonal model ARIMA(4，1，1)(1，1，1)12.The diagnostic test showed that this model had good fitting results of forecasting the number of books borrowing，Finally，this model was applied to predict the books borrowing form January to June of 2010，and the result preferably fit the actual situation.

multiplicative seasonal model;time series;books borrowing;forecast

G250.7

A

1672-7169(2011)03-0105-04

2011-02-01

劉琳(1968-)，女，華北科技學院圖書館教師。