高等數學中反例教學研究①

王 濤 于艷華

(華北科技學院基礎部，北京東燕郊 101601)

高等數學中反例教學研究①

王 濤1②于艷華

(華北科技學院基礎部，北京東燕郊 101601)

本文對高等數學中的反例進行了探討和研究，論述了反例的類型及構造，給出了高等數學中一些典型的反例，并進行了詳細的分析，說明了反例在高等數學教學中的重要作用以及應注意的一些問題。

高等數學;數學研究;反例

高等數學是本科工程類各專業必修的重要的公共基礎理論課之一，通過該課程的學習，要求學生系統地獲得:一元函數微積分學;常微分方程;多元函數微積分學;無窮級數等方面的基本知識和基本運算技能，為學習后續課程奠定必要的數學基礎。在學習過程中逐步培養學生抽象與概括問題的能力，邏輯推理能力，空間想象能力以及綜合運用所學知識分析問題和解決問題的能力。

數學中的反例是指符合某個命題的條件，但又與該命題結論相矛盾的例子，也即指出某命題不成立的例子。在數學的發展史中，反例在數學的發展過程中有著重要的地位和作用，大到能推動一個學科的發展或否定上百年的猜想，例如:畢達哥拉斯學派證明了勾股定理的同時，也得到了一些直角三角形的三邊比不能用整數來表達，也就是勾長或股長與弦長是不可通約的。這樣一來，就否定了畢達哥拉斯學派的信條:宇宙間的一切現象都能歸結為整數或整數之比。不可通約性的發現引起第一次數學危機，直接導致了歐幾里得的《幾何原本》的產生。小至能夠準確理解一個定義和概念。

教育部于2003年制定的《數學課程標準》中指出:“人們在學習數學和運用數學解決問題時，不斷地經歷直觀感知、觀察發現、歸納類比、空間想象、抽象概括、符號標示、運算求解、數據處理、演繹證明、反思與建構等思維過程。”反思過程是數學辯證邏輯思維能力的一種具體體現。而反例是鍛煉反思能力的最好形勢之一。

在傳統的高等數學教學中，往往注重基本概念、定義的講解、定理的證明、公式的推導及典型例題的計算，而忽視高等數學中反例的教學研究與應用，造成多數學生雖能熟練地計算高等數學的習題，了解一些定理形式上的證明，卻不能清楚弱化定理條件，造成命題錯誤的根本原因。

下面我們對高等數學中反例的類型及實例進行探討，給出高等數學中一些典型的反例，并進行教學分析。說明反例在高等數學教學中的重要地位和作用。

1 高等數學中反例的類型及實例

1.1 由定義產生的反例

概念是數學學科的細胞，是反映事物本質的思維形式。在邏輯學中，定義是明確概念內涵的邏輯方法。在數學問題中，若首先給出一個概念的定義，然后判斷一個猜想是否正確，反例的獲得常常需要從定義入手。

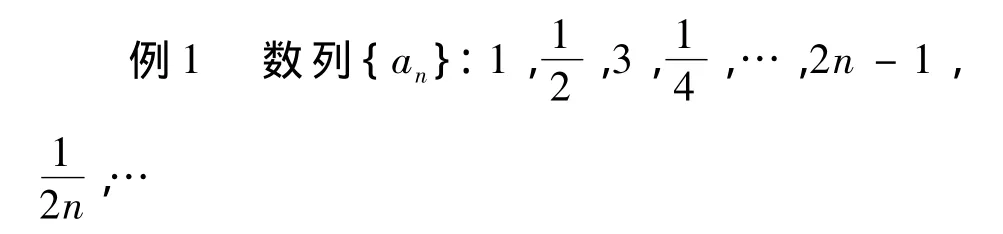
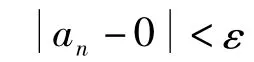
容易知道，an是無界變量，但當n→∞時，an不是無窮大量。例1說明無界變量和無窮大量有著本質區別。

1.2 由逆命題產生的反例

高等數學中的一些命題的條件和結論有著緊密聯系，卻是非等價的。其逆命題往往不成立。

命題:數列收斂必有界，逆命題:有界數列必收斂。

例2 數列{an}:-1，1，-1，1，…，(-1)n，…有界，但不收斂。

命題:可導一定連續，逆命題:連續一定可導。

1.3 弱化定理條件產生的反例

例4(羅爾定理)如果函數f(x)滿足

(1)在閉區間［a，b］上連續;(2)在開區間(a，b)內可導;(3)在區間端點處函數值相等，即f(a)=f(b)，那么在(a，b)內至少存在一點 ξ，使得 f'(ξ)=0。

A.函數f(x)滿足條件(2)(3)，但不滿足條件(1)。

B.函數f(x)滿足條件(1)(3)，但不滿足條件(2)。

C.函數f(x)滿足條件(1)(2)，但不滿足條件(3)。

例4.3 設 f(x)=x，0 ≤x≤1，則函數 f(x)在閉區間［0，1］上連續;在開區間(0，1)內可導;在區間端點處函數值不相等，而當 x∈(0，1)時，f'(x)=1≠0。

例4.1-4.3說明羅爾定理中的三個條件缺一不可。

1.4 有限和無窮相互轉變產生的反例

有限個無窮小量之和(積)是無窮小量。但對于無限個無窮小量之和(積)可以不是無窮小量。

2 反例研究在高等數學教學中的作用

2.1 準確理解定義和概念

定義和概念在高等數學中占有重要的地位，它是進行邏輯推理的基礎.但學生在初學高等數學時，常常重視定理、公式的應用和解題方法的訓練，而對定義沒有給予足夠的重視.使用這種學習方法學習高等數學，將會產生概念不清或死記硬背定義而不能真正掌握概念的內涵等情況.使得學生在做和定義、概念相關的選擇題和判斷題目時，常常出現錯誤。例如在學生開始學數列極限的定義時，常常對極限的定義不清楚，認為極限中ε-N語言是形式的而非本質的，錯誤地認為極限定義中的“所有”改為“無窮多個”等價，描述性語言中的“無限接近”與“逐漸接近”是等價的。還有些學生混淆無界變量和無窮大量的定義。在教學中我們可以通過本文中例1來解決這些問題。

通過構造恰當的反例，可以從反面消除一些容易出現的模糊認識，有助于學生嚴格區分那些相近易混的概念，認清概念的本質。

2.2 正確掌握定理和命題

定理在高等數學中的有著舉足輕重的作用.由于高等數學中的定理眾多，大多數定理不易找出幾何或物理模型，學生要正確掌握定理有一定的難度.反例可以幫助學生明確定理的正確使用范圍。在命題學習中，用生動的反例駁斥錯誤的命題是非常簡潔、有效的。更重要的是，反例可用來說明命題的使用范圍。這對初學者來說是非常有益的，不僅能澄清一些錯誤的認識，還能促使學生養成嚴密推理、重視條件的習慣，避免發生“簡單”卻“致命”的錯誤。

掌握反例可以加強對定理條件的正確理解，例如若掌握了我們給出的例4.1-4.3就可清楚的知道羅爾定理的條件缺一不可。掌握反例還可以加強對定理和命題內涵的正確理解。

2.3 正確理解有限與無限的區別

從哲學上講，有限和無限是物質世界存在的客觀矛盾，是物質的運動在時間和空間上表現出來的的辯證聯系，有限和無限的關系是辯證的，是對立統一的。其具體表現為，無限由有限構成，無限不能脫離有限而獨立存在，有限也包含無限，有限體現著無限。

學習高等數學，需要掌握有限與無限的聯系與區別.首先要學會使用運動的觀點，通過有限認識無限;其次要明確有限與無限本質上的區別和聯系.對這兩個問題，多數教材沒有在理論上給出詳細的論述，加上學生受中學思維定勢(有限條件下)的影響，不注意有限與無限的區別，常常誤認為在“有限”的條件下成立的命題在“無限”的條件下也同樣成立.我們可以通過反例幫助學生糾正這種錯誤觀念.例如我們在自然數集N={0，1，2，…}和其真子集 M={0，2，4，…}可以建立一一映射f:x?2x，而在有限集上不可能和其真子集建立一一映射。有限個無窮小量之和(積)是無窮小量，而通過反例2，可以讓學生清楚地看到把命題中的“有限”改成“無限”是錯誤的。

2.4 反例有助于提高學生的數學素養

數學由證明和反駁兩大類組成，數學的發展也是朝著提出證明和構造反例這兩個主要目標前進的。構造反例具有一定的技巧性。它不僅與基礎知識的掌握程度有關，還涉及思維的發散程度，知識面的寬窄等。反例的構造過程是一項積極的、具有創造性的思維活動，是一個探索發現的過程。重視和體驗這樣的過程，不僅能拓寬思路，活躍思維，激發學生的求知欲，培養學生思維的嚴密性，提高自學能力，也能提高學生分析問題、解決問題的能力，有助于學生克服思維定式，提高其思維能力和數學素養。

3 反例教學中要注意的問題

在現有的高等數學中反例五花八門，層次高低不同。作為高校教師，掌握以下兩個類型的反例是必要的。一類是構造起來較困難，課堂上基本不用，但課下少數有興趣的學生可能涉及，屬教師應用型。另一類是構造起來簡單易行，卻能很好說明問題，屬課堂教學應用型，如為了說明連續不一定可導，我們常用本文列舉的反例3。在高等數學教學中應用反例來說明問題，首先要注意反例的選取，選擇的反例要簡單易行，若選取較艱澀的反例，會適得其反，造成學生更多的困惑。其次，在教學中要通過創設問題的情境，啟發學生興趣，鼓勵學生自己構造反例，從而達到教學目的。

［1］ 杜春雨.高等數學中反例的研究［J］.高等數學研究.2008，11(5):26-27

［2］ 唐敏.反例在高等數學中的作用［J］.西南民族學院學報(自然科學版)，1997，11(4):461-464

［3］ 丁秀梅.反例在高等數學教學中的作用初探［J］.江蘇經貿職業技術學院學報，2004，(1)

［4］ 朱勇等.高等數學中的反例［M］.武漢:華中工業出版社，1998

［5］ 同濟大學數學系.高等數學(第六版)［M］.北京:高等教育出版社，2007

Study on contrary cases in higher mathematics

WANG Tao，YU Yanhua

(Department of Basic Course，North China Institute of Science and Technology，Yanjiao Beijing-East101601)

This paper holds an exploration on contrary cases in higher mathematics by focusing on the types and conformation.It also gives some typical contrary cases in higher mathematics studying and makes detailed analysis in them，demonstrating the important functions of contrary cases in higher mathematics and some problems worth paying attention to.

higher mathematics;mathematics research;contrary cases

G40-034

A

1672-7169(2011)03-0095-03

2011-06-03。基金項目:華北科技學院教育科學研究資助項目(Jkzd11-17)。

王濤(1972-)男，河北遷安人，碩士，華北科技學院基礎部副教授，研究方向:圖論。