一類改進(jìn)的Ostrowski方法*

于雙紅， 何國龍

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院，浙江金華 321004)

0 引言

求解非線性方程是數(shù)值計(jì)算中一個(gè)非常重要的問題，本文考慮求解非線性方程f(x)=0單根的迭代法，其中f:D?R→R是一個(gè)單值非線性函數(shù)，D為實(shí)數(shù)域上的一個(gè)開區(qū)間．

2階收斂的牛頓法是解非線性方程最重要也是最基礎(chǔ)的方法之一，其效率指數(shù)為1．414，迭代格式為

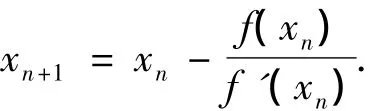
近年來，為更快、更精確地求得非線性方程的近似解，在牛頓法的基礎(chǔ)上作了一系列的改進(jìn)，得到一些著名的方法．例如 Jarratt方法［1-2］、Chebyshev-Halley 方法［3］和 Ostrowski方法［4-11］．4 階收斂的 Ostrows-ki方法要求計(jì)算2個(gè)函數(shù)值和1個(gè)一階導(dǎo)數(shù)值，其效率指數(shù)為1．587，迭代格式為

文獻(xiàn)［5］和文獻(xiàn)［6］分別得到一類收斂階為6的Ostrowski改進(jìn)方法，其效率指數(shù)為1．565，迭代格式分別為:

和

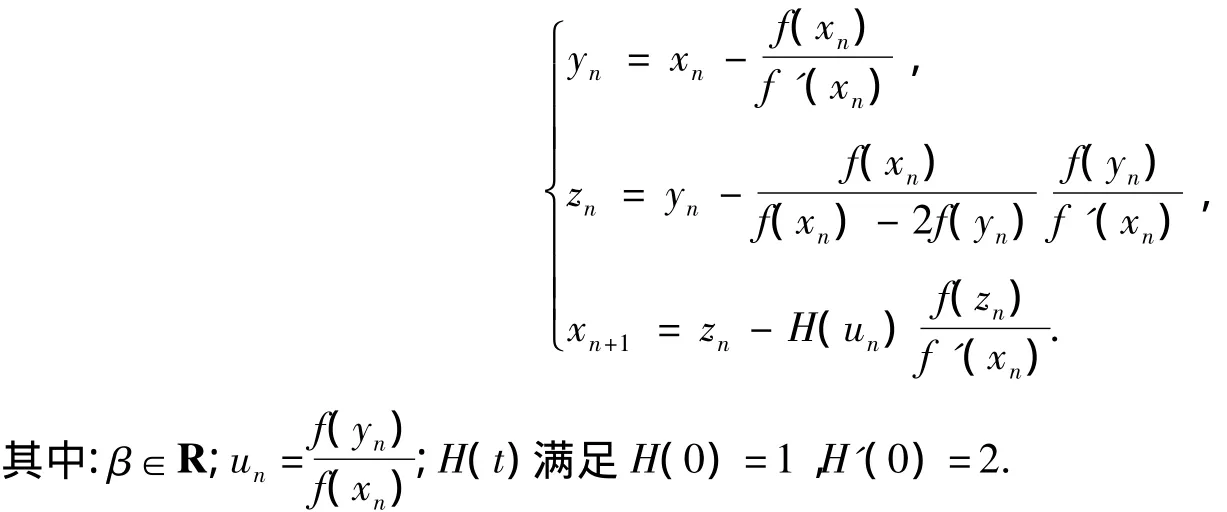
文獻(xiàn)［7］提出了一類收斂階為7的改進(jìn)的Ostrowski方法，效率指數(shù)為1．627，迭代格式為

文獻(xiàn)［8］提出了收斂階為8的改進(jìn)的Ostrowski方法，其效率指數(shù)為1．682，迭代格式為

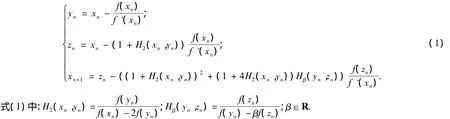
文獻(xiàn)［10］提出了收斂階為8的改進(jìn)的Ostrowski方法，迭代格式為

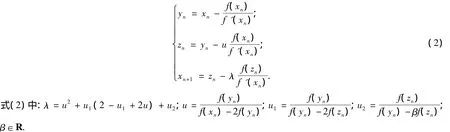
文獻(xiàn)［11］也提出了收斂階為8的改進(jìn)方法，迭代格式為

本文提出的一類新的改進(jìn)Ostrowski方法，每一步迭代只需求3個(gè)函數(shù)值和1個(gè)一階導(dǎo)數(shù)值，并從理論上、試驗(yàn)中證明新方法的收斂階為8．

1 相關(guān)概念

定義1［12］設(shè)α是充分光滑函數(shù) f:D?R→R的單根，D是開區(qū)間，并假設(shè)迭代序列{xn}(n=0，1，2，…)收斂于 α，且存在p≥1及常數(shù)C＞0，使得當(dāng) k≥k0時(shí)，‖xn+1－α‖≤C‖xn－α‖p，則稱序列{xn}至少p階收斂，稱C為漸進(jìn)誤差常數(shù)．當(dāng)p=1，0＜α＜1時(shí)，稱序列{xn}至少線性收斂;當(dāng)p=2，α＞0時(shí)，稱序列{xn}為至少平方收斂．設(shè)en=xn－α，則稱關(guān)系式en+1=Cepn+O(ep+1n)為誤差方程，稱p為收斂階．

定義2［12］若一個(gè)收斂于α的序列{xi}i∈N的收斂階為p，每迭代一步的工作量為w，則稱e=p1/w為效率指數(shù)．

定義3［12］設(shè) xn+1，xn，xn－1(n=1，2，…)是根 α 附近的3個(gè)連續(xù)的迭代值，則收斂階近似地表示為

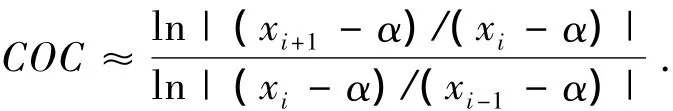
2 主要結(jié)果

本文主要考慮如下迭代式:

式(3)中:

定理1 設(shè)函數(shù)f:D?R→R有單根α∈D，D為開區(qū)間，f(xn)在α附近足夠光滑，W(t，s)是滿足W(0，0)=1，Wt(0，0)=1，Ws(0，0)=0，|Wtt(0，0)|＜∞，|Wts(0，0)|=|Wst(0，0)|＜ ∞，|Wss(0，0)|＜∞的實(shí)函數(shù)，則由式(3)和式(4)定義的迭代方法的收斂階為8．

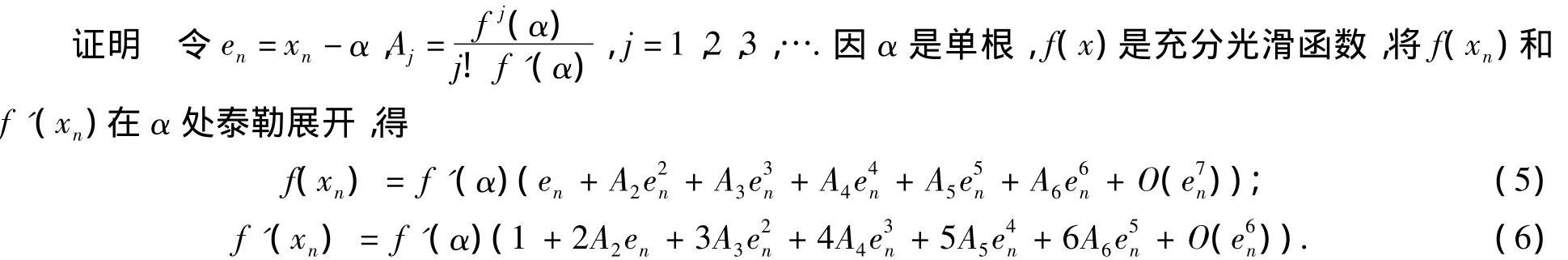
經(jīng)Maple計(jì)算得

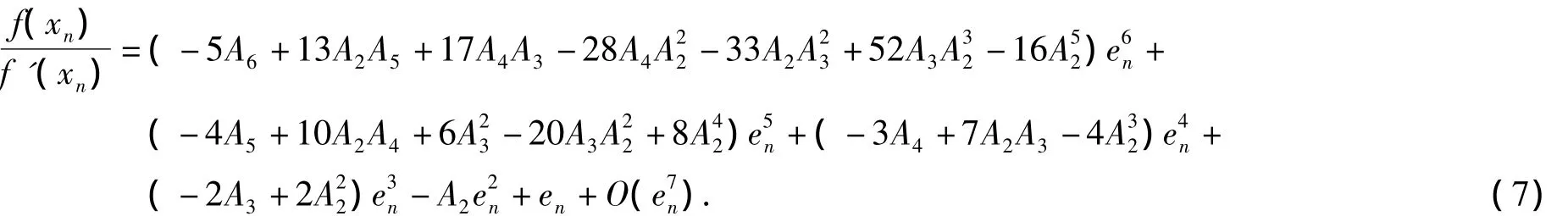
將f(yn)在α處泰勒展開，得

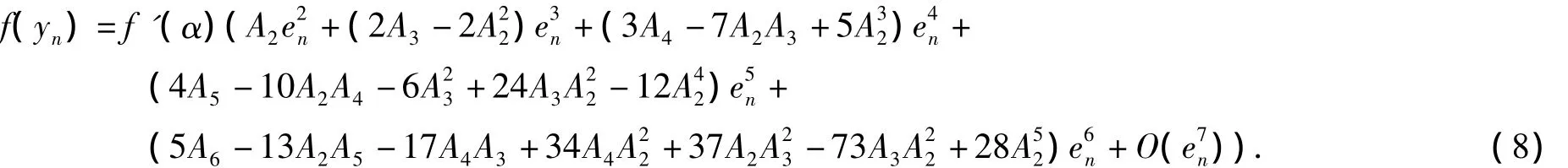
由式(5)～式(8)得

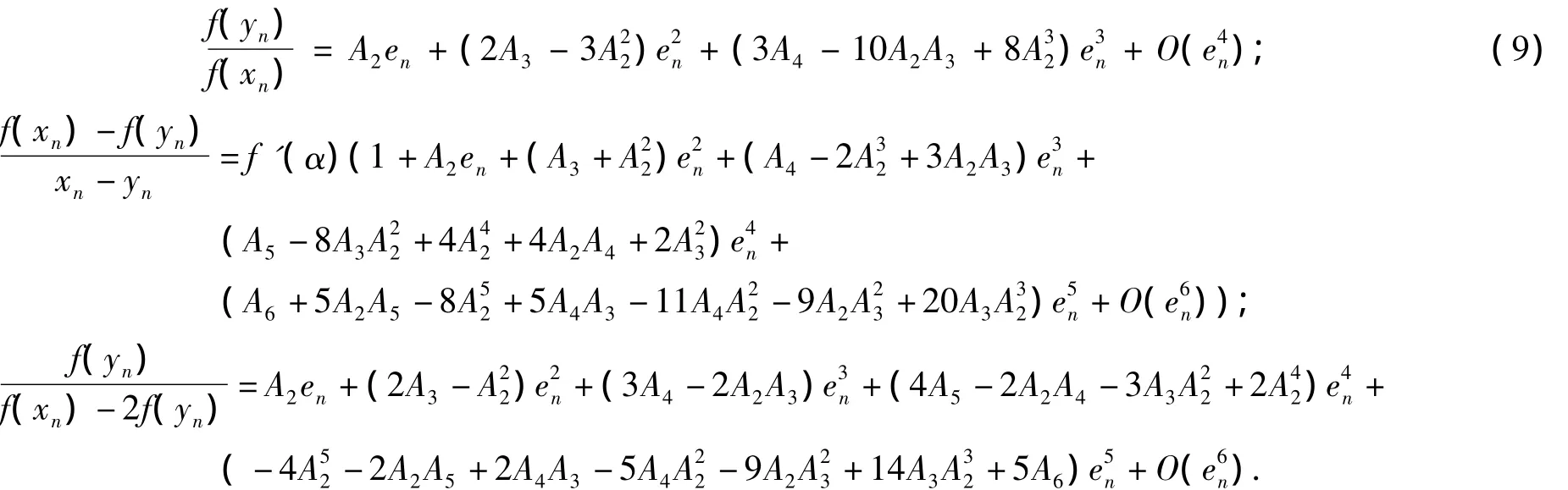
則

因而

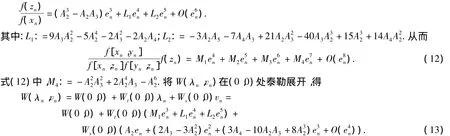
由式(10)～式(13)可得

即

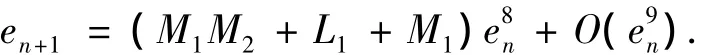
定理1證畢．

由定理1，可以將式(3)進(jìn)一步一般化，得到迭代式

式(15)中，λn，vn的意義與式(4)相同．

定理2 設(shè)函數(shù)f:D?R→R有單根α∈D，D為開區(qū)間，f(xn)在α附近足夠光滑，H(u)是滿足H(0)=0，H'(0)=1，H"(0)=4，H(3)(0)=24 的實(shí)函數(shù)，W(t，s)是滿足 W(0，0)=1，Wt(0，0)=1，Ws(0，0)=0，|Wtt(0，0)|＜∞，|Wts(0，0)|=|Wst(0，0)|＜ ∞，|Wss(0，0)|＜ ∞ 的實(shí)函數(shù)，則由式(15)定義的迭代方法的收斂階為8．

證明 將H(vn)在0處泰勒展開，得

則

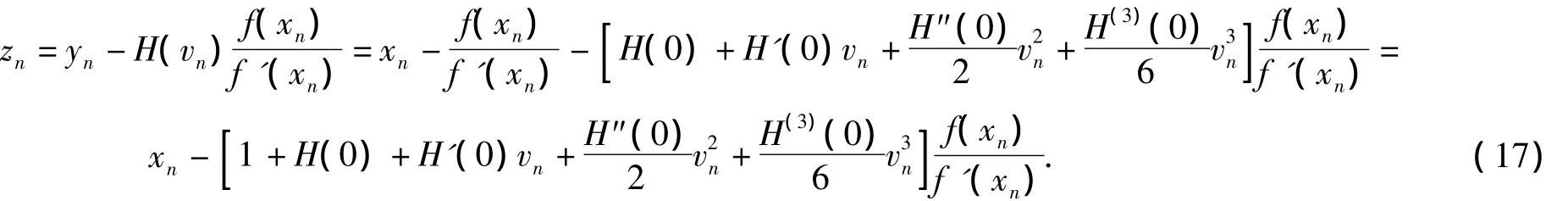
將式(9)代入式(17)得

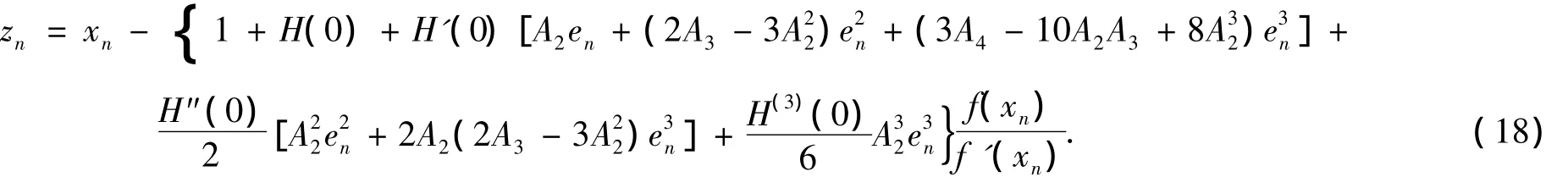
化簡式(18)得

令 H(0)=0，H'(0)=1，H"(0)=4，則 zn= α +LX．其中

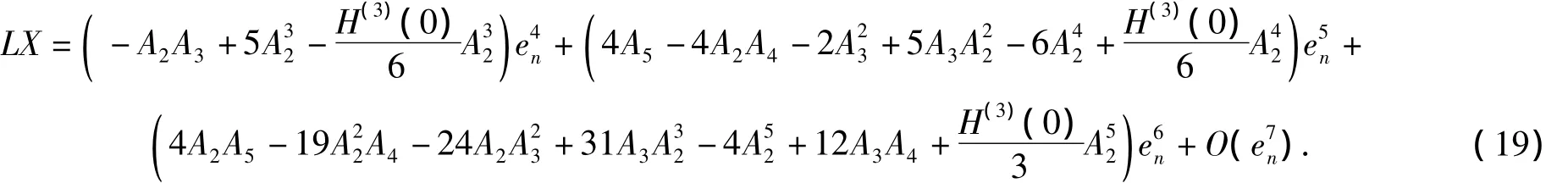
因此

由式(9)、式(20)和式(21)可得

其中:

令 γ1=0，γ2=0，γ3=0，γ4=0，則

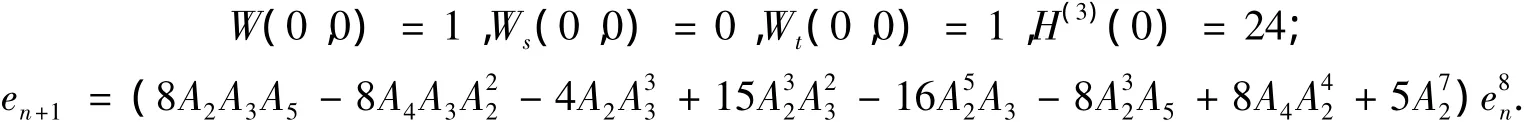
定理2證畢．

例 1 取 W(t，s):=1+t+ αts，則

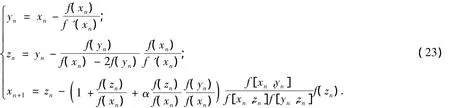
式(23)中，α∈R．誤差方程為

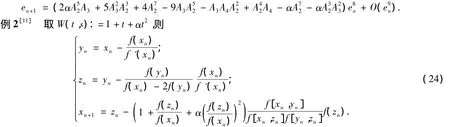
式(24)中，α∈R．誤差方程為27234589

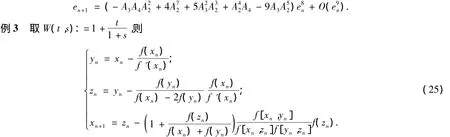
誤差方程為

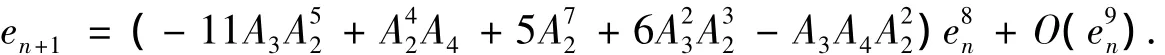
由式(3)、式(4)和式(15)定義的方法每一步迭代需要計(jì)算3個(gè)函數(shù)值和1個(gè)一階導(dǎo)數(shù)值，根據(jù)定義2，新定義的迭代方法的效率指數(shù)是81/4≈1．682，均高于Ostrowski方法的效率指數(shù)41/3≈1．587，6階改進(jìn)方法［4-6］的效率指數(shù)61/4≈1．565 及7 階的改進(jìn)方法［7］效率指數(shù)71/4≈1．627．

3 數(shù)值試驗(yàn)

下面將通過數(shù)值試驗(yàn)比較各方法的差異．考慮式(1)、式(2)和式(23)～式(25)5種8階迭代法(α=1，β=1)，所有的計(jì)算均在800位精度Maple 14下進(jìn)行操作，被測函數(shù)在不同的方法中均迭代3次后得到的xn－α和|fi(xn)|及COC如表1所示．選擇的被測函數(shù)為:

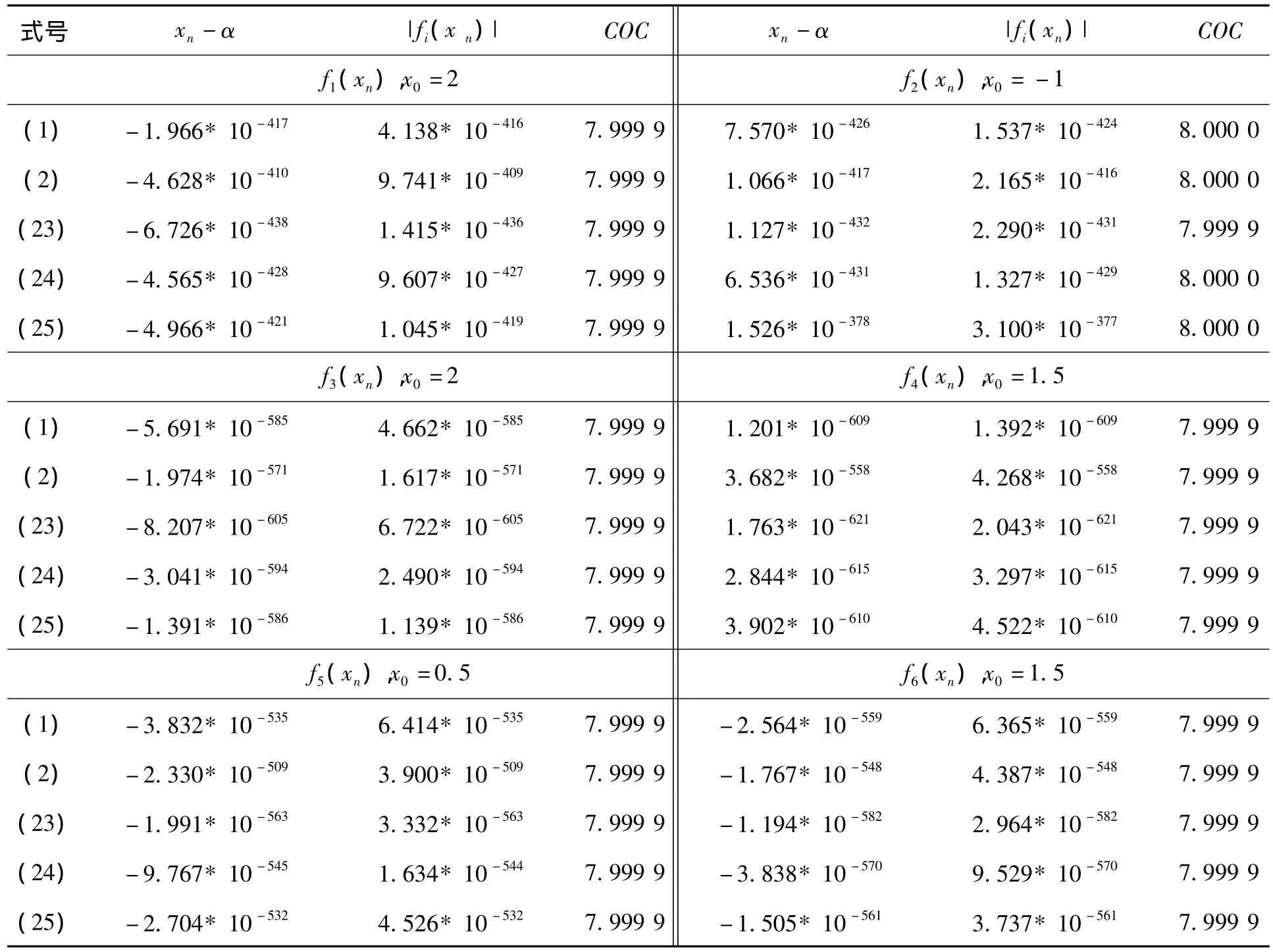
表1 迭代3次得到的xn－α和|fi(xn)|及COC

從表1可以看出，在相同的計(jì)算量、相同的界下，本文提出的方法是有效的．

［1］Kou J S，Li Y T．An improvement of the Jarratt method［J］．Applied Mathematics and Computation，2007，189(2):1816-1821．

［2］Ren Hongmin，Wu Qingbiao，Bi Weihong．New variants of Jarratt's method with sixth-order convergence［J］．Numer Algor，2009，52(4):585-603．

［3］Li Yaotang，Zhang Peiyuan，Li Yanyan．Some new variants of Chebyshev-Halley methods free from second derivative［J］．International Journal of Nonlinear Science，2010，9(2):201-206．

［4］Miquel G，José Luis D B．An improvement to Ostrowski root-finding method［J］．Applied Mathematics and Computation，2006，173(1):450-456．

［5］Sharma J R，Guha R K．A family of modified Ostrowski methods with accelerated sixth-order convergence［J］．Applied Mathematics and Computation，2007，190(1):111-115．

［6］Changbum C，Yoonmee H．Some sixth-order variants of Ostrowski root-finding methods［J］．Applied Mathematics and Computation，2007，193(2):389-394．

［7］Kou Jisheng，Li Yitian，Wang Xiuhua．Some variants of Ostrowski's method with seventh-order convergence［J］．Journal of Computational and Applied Mathematics，2007，209(2):153-159．

［8］Kou Jisheng，Wang Xiuhua．Some improvements of Ostrowski's method［J］．Applied Mathematics Letters，2010，23(1):92-96．

［9］Kou Jisheng．Some new root-finding methods with eighth-order convergence［J］．Sci Math Roumanie Tome，2010，53(2):133-143．

［10］Zhang G F，Zhang Y X．New family of eighth-order methods for nonlinear equation［J］．COMPEL，2009，28(6):1418-1427．

［11］Sharma J R，Sharma J N．A new family of modified Ostrowski's methods with accelerated eighth order convergence［J］．Numer Algor，2010，54:445-458．

［12］Burden R L，F(xiàn)aires J D，Reynolds A C．Numerical analysis［M］．Boston:Prindle，Weber Schmidt，1981．