關(guān)于弱λ-Koszul模極小分次投射分解的一個注記*

樂陶軍， 陳淼森

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院，浙江金華 321004)

0 引言

Koszul代數(shù)是Priddy［1］在1970年提出的．此后，在一大批數(shù)學(xué)工作者的努力下，Koszul代數(shù)得到了多方面經(jīng)典的推廣．例如 d-Koszul代數(shù)(模)［2］，弱 d-Koszul代數(shù)(模)［3］，(弱)λ-koszul代數(shù)(模)［4］等．文獻［4］已證明了任意弱λ-Koszul模都可以由λ-Koszul模來逼近．設(shè)A是λ-Koszul代數(shù)，M是有限生成的 A-模，又設(shè) Sd0，Sd1，…，Sdp是 M 的極小齊次生成元集，記 Ui:=〈Sd0，Sd1，…，Sdi〉．易見，M 有自然的分次子模濾

則M是弱λ-Koszul模當且僅當商模Ui/Ui－1(0≤i≤p)都是λ-Koszul模，其中U－1=0．

本文對λ-Koszul模和弱λ-Koszul模作進一步討論．設(shè)M為弱λ-koszul模，令Pi*→Ui/Ui－1→0和P*→M→0分別是對應(yīng)的極小分次投射分解．以極小馬蹄型引理為主要研究工具，討論了Pi*和P*的關(guān)系，得到了如下主要結(jié)果:

定理1 令M是弱λ-Koszul模，F(xiàn) M是M的自然的分次子模濾，Pi*→Ui/Ui－1→0和P*→M→0(i=1，2，…，p)分別是對應(yīng)的極小投射分解，則對n≥0，有

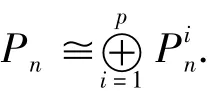
其中，Pn和Pin分別是極小分次投射分解P*和Pi*的第n項．

為方便起見，本文約定:k表示一個任意的域;N和Z分別表示自然數(shù)集和整數(shù)集;非負標準分次k的i≥0，Ai是有限維的k-空間．J表示分次代數(shù)A的分次Jacobson根;Gr(A)和gr(A)分別表示分次A-模范疇和有限生成分次A-模范疇．

1 (弱)λ-Koszul模的定義

令λ:N→N是個周期函數(shù)，記它的最小正周期為|λ|．假設(shè)λ(1)≥2，且λ在區(qū)間［1，|λ|］上嚴格單調(diào)增．設(shè)δλ:N→N是另一函數(shù)，且具有以下性質(zhì):

定義1［4］令M∈gr(A)，若存在一個極小分次投射分解

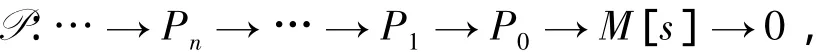
使得Pn(n≥0)都由δλ(n)次生成，則稱M是λ-Koszul模．其中:［·］是平移函子;s是一個固定的整數(shù)．特別地，若平凡模A0是 λ-Koszul模，則稱分次代

令‖A‖:=|λ|=T，通常稱‖A‖為A的跳躍度．顯然，當|λ|=1時，λ-Koszul代數(shù)就是d-Koszul代數(shù)，也就是說，d-Koszul代數(shù)是λ-Koszul代數(shù)的一個特例．

定義2［4］令A(yù)是λ-Koszul代數(shù)，且‖A‖=T≥1，M∈gr(A)．若存在一個關(guān)于M的極小分次投射分解

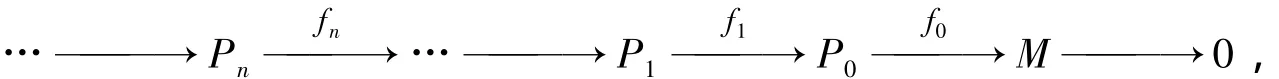
使得對 i，k≥0，有

1)當 i≡2n(mod 2T)，n∈［0，T －1］時，ker fi?JPi且 Jkker fi=Jk+1Pi∩ker fi，

2)當 i≡2n －1(mod 2T)，n∈［1，T］時，ker fi?Jλ(n)Pi且 Jkker fi=Jλ(n)+kPi∩ker fi，則稱M是弱λ-Koszul模．

2 定理1的證明

首先給出幾個引理．

引理1［5］令0→K→M→N→0是有限生成A-模正合列，則以下結(jié)論等價:

1)JkK=K∩JkM(k≥0);

2)A/Jk?AK→A/Jk?AM 是單同態(tài)(k≥0);

3)0→JkK→JkM→JkN→0是正合的(k≥0);

4)0→JkK/Jk+1K→JkM/Jk+1M→JkN/Jk+1N→0是正合的(k≥0);

5)0→JkK/JmK→JkM/JmM→JkN/JmN→0是正合的(m＞k)．

引理2［4］令A(yù)是分次代數(shù)，0→K→M→N→0是有限生成A-模正合列，則JK=K∩JM當且僅當有行列正合交換圖1．

圖1 行列正合交換圖1

其中:P0，L0，Q0是 K，M，N 的分次投射蓋;Ω1(K)，Ω1(M)，Ω1(N)分別是 K，M，N 的合沖．

證明 充分性 首先由引理1得正合列

注意到對任意有限生成A-模M，A?A0M/JM→M→0為投射蓋．現(xiàn)令P0:=A?A0K/JK，L0:=A?A0M/JM，Q0:=A?A0N/JN．由A0半單得0→P0→L0→Q0→0正合且可裂，因此得交換圖1．

必要性 若圖1成立，則得正合列0→P0→L0→Q0→0．注意到在同構(gòu)意義下投射蓋是唯一的，設(shè)P0:=A?A0K/JK，L0:=A?A0M/JM，Q0:=A?A0N/JN，則

從而得正合列0→K/JK→M/JM?N/JN→0．由于A0是半單的，故有JK=K∩JM．

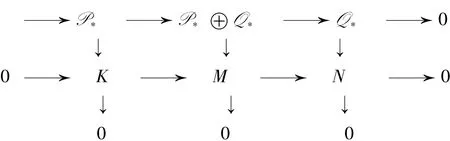
圖2 行列正合交換圖2

證明 由引理3得JK=K∩JM，從而得與引理2相同的行列交換圖1．由引理2的證明得0→P0→L0→Q0→0 是可裂的，因此，L0?P0⊕Q0．

注意到 Ω1(K)?JP0，Ω1(M)?JL0，Ω1(N)?JQ0，從而有行列正合交換圖3．

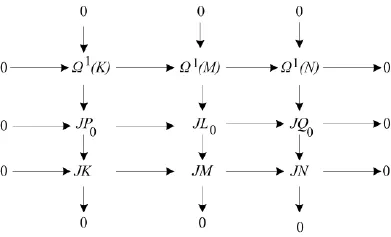
圖3 行列正合交換圖3

將函子A/J?A作用于圖3，又因M，N都是弱λ-Koszul模，故可得交換圖4．

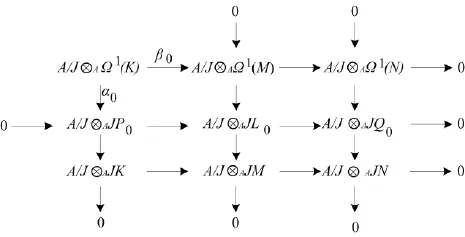
圖4 行列正合交換圖4

根據(jù)引理3的1)知K是λ-Koszul模，從而又由引理3的2)得JΩ1(K)=Ω1(K)∩J2P0，再由引理1知α0是單同態(tài)，所以由3 ×3 引理［7］得 β0也是單同態(tài)，因此 J Ω1(K)=Ω1(K)∩JΩ1(M)．

繼續(xù)應(yīng)用引理2，可得行列正合交換圖5．

圖5 行列正合交換圖5

同樣，0→P1→L1→Q1→0 是可裂的，從而有 L1?P1⊕Q1．因 Ω2(K)? Jλ(1)P1，Ω2(M)?Jλ(1)L1，Ω2(N)?Jλ(1)Q1，故有行列正合交換圖 6．

圖6 行列正合交換圖6

其中:P1，L1，Q1分別是 Ω1(K)，Ω1(M)，Ω1(N)的分次投射蓋;Ω2(K)，Ω2(M)，Ω2(N)分別是 K，M，N 的二次合沖．

將函子A/J?A作用于圖6，注意到K是λ-Koszul模，且M，N是弱λ-Koszul模，從而有交換圖7．

圖7 行列正合交換圖7

因 K 是 λ-Koszul模，故 JΩ2(K)=Ω2(K)∩Jλ(1)+1P1，再由引理1得 α1是單同態(tài)，所以由3 ×3 引理［7］知β1也是單同態(tài)，因此，JΩ2(K)=Ω2(K)∩JΩ2(M)．

重復(fù)以上操作，即可證得引理4．

最后得定理1的證明．

證明 首先對于短正合列0→U1→M→M/U1→0，根據(jù)引理4，可得行列正合交換圖8．

圖8 行列正合交換圖8

其中，P1*，P*，L1*分別是U1，M，M/U1的極小分次投射分解．易得0→P1*→P*→L1*→0是可裂的，從而 P*?P1*⊕L1*．記 W=M/U1，則〈Wd2〉=U2/U1=K2．再對短正合列0→K2→W→W/K2→0 進行討論．根據(jù)引理4，可得行列正合交換圖9．

同樣，L1*?P2*⊕L2*．其中，P2*，L1*，L2*分別是 K2，W，W/K2的極小分次投射分解．

重復(fù)以上過程，可得行列正合交換圖10．

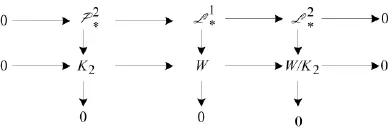
圖9 行列正合交換圖9

圖10 行列正合交換圖10

［1］Priddy S．Koszul resolutions［J］．Trans Amer Math Soc，1970，152(1):39-60．

［2］Green E L，Marcos E N，Martinez-Villa R，et al．D-Koszul algebras［J］．J Pure Appl Alg，2004，193(1/2/3):141-162．

［3］Lü Jiafeng，Wang Guojun．Weakly d-Koszul modules［J］．Viet J Math，2006，34(3):341-351．

［4］Lu Jiafeng．Algebras with periodic shifts of ext degree［J］．Math Notes，2009，86(5/6):665-681．

［5］呂家鳳，何濟偉，盧滌明．具有 d-Koszul子模濾的分次模［J］．數(shù)學(xué)年刊，2007，28A(2):231-238．

［6］Lü Jiafeng．On modules with d-Koszul-type submodules［J］．Acta Math Sin:Engl Ser，2009，25(6):1015-1030．

［7］佟文廷．同調(diào)代數(shù)引論［M］．北京:高等教育出版社，1998:178-180．