小型電視制導空地彈大落角導引律設計方法*

陳華兵,彭勤素,楊明星,吳勝男

(中國航天科技集團第四研究院第41所燃燒、流動和熱結構國家級重點實驗室,西安 710025)

0 引言

采用電視制導的空地導彈為適應無人機作戰的需求,均向小型化、多用途發展,如美國的小“長釘”、“海爾法”,PAM、聯合空地導彈 JAGM,以色列SPIKE家族的新增成員 SPIEK-NLOS導彈,德國IDAS導彈等。該類導彈攻擊的典型目標包括裝甲型和地面工事等防御型,通常采用穿甲或侵徹戰斗部,為達到最佳的穿透能力,一般要求導彈采用大落角攻擊方式,由此提高了對導彈和彈上設備的性能要求,主要有以下幾個方面:

a)要求在較小的結構尺寸下盡量增大導引頭的下視框架角,以滿足導彈在機動過程中對目標的凝視要求;

b)要求導引頭識別距離和工作高度盡量大,保證導彈有足夠的制導時間,盡量增大落角;

c)要求導彈質量小、升阻特性好,盡量提供大的可用過載,在實現大落角攻擊的同時保證較小的脫靶量。

然而,在導彈總體設計時,以上性能一般不能同時達到最優,因此,需通過導引律設計尋求滿足各方面約束的制導方案。

1 常見的大落角攻擊制導方案

1.1 框架角門限+比例導引

框架角門限是指導彈平飛時,隨著彈目距離的減小,彈目視線角增加,導引頭對目標凝視所需的框架角逐漸增加,當增加至某一定值時,轉入比例導引進行俯沖攻擊,其理論軌跡見圖1。

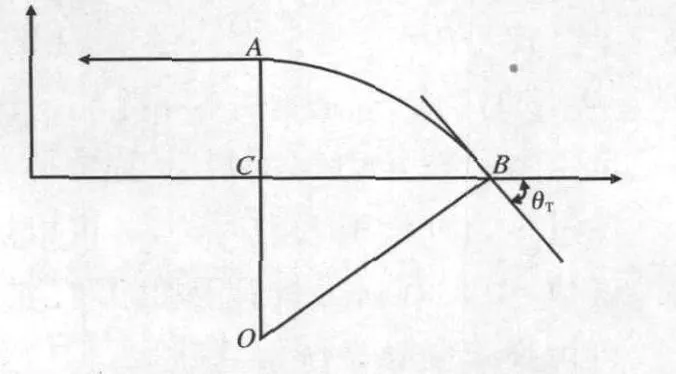
圖1 框架角門限+比例導引的理論軌跡

假設導彈以質點考慮,俯沖攻擊時速度不變,可知導彈以最大可用過載俯沖攻擊時為末制導極限轉彎半徑,則:

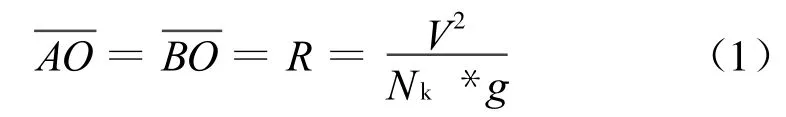
式中:Nk為可用過載;R為轉彎半徑;V為導彈速度。

∠AOB大小等于落角大小,可得:

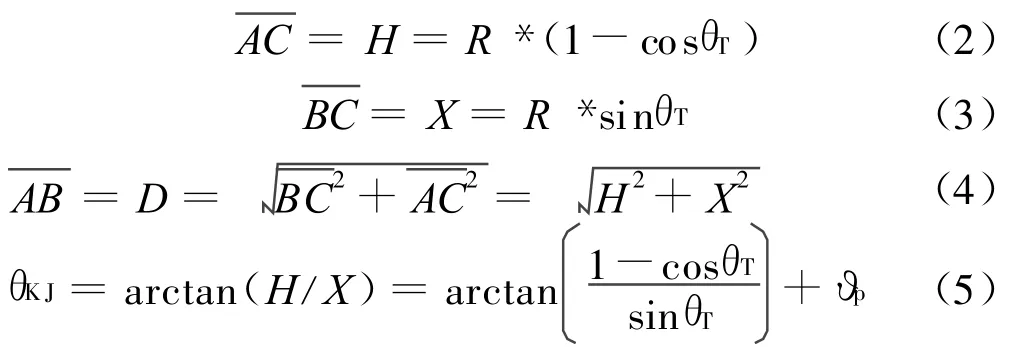
式中:θT為落角,H為導彈平飛高度,X為彈目射向距離,D為彈目斜距,θKJ為導引頭框架角,?p為平飛俯仰角。由式(1)～式(5)可知,當給定導彈速度、可用過載和落角要求時,不考慮?p,可計算出末制導起點彈道高度、彈目距離和框架角理論下限,再根據末制導比例導引的過載利用率對理論下限進行修正,可得實際的約束條件,在此基礎上結合導彈性能進行末制導律設計。

1.2 帶過重力補償的比例導引

在縱向制導回路中為消除重力的影響,通常引入重力補償,當加在制導指令上的重力補償指令超過重力影響時,稱之過重力補償。

在比例導引回路中加入過重力補償信號,就會使彈道在比例導引初始階段向上抬起,同時又由于閉環比例導引律的作用使彈道向回拉,這樣彈道末段傾角就會增大,從而增大導彈的落角。帶過重力補償的制導回路簡化數學模型見圖2。

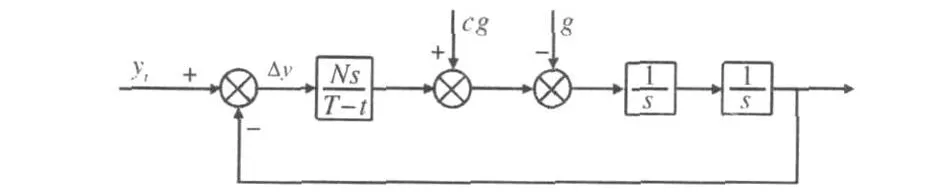
圖2 過重力補償制導回路簡化數學模型

模型中cg為重力補償項,c為重力補償系數,當c=1時為正常重力補償,當c＞1時為過重力補償。過重力補償導引律的設計主要是補償系數c的取值和過重力補償引入的時刻,c可取定值或其他參數的函數,引入時刻可按彈目距離門限值判斷,彈目距離可由彈上制導系統解算獲取,但應注意彈目距離預估可以偏小但不能偏大,以免需用過載偏大造成較大脫靶。

1.3 帶落角補償的比例導引

由于采用比例導引時,導彈速度方向收斂于彈目視線方向,如果將視線調整至導彈需求落角對應的方向上,即可實現導彈沿需求落角方向進行俯沖攻擊。因此,將落角與視線角的偏差引入制導指令,對比例導引進行補償,制導回路數學模型見圖3。

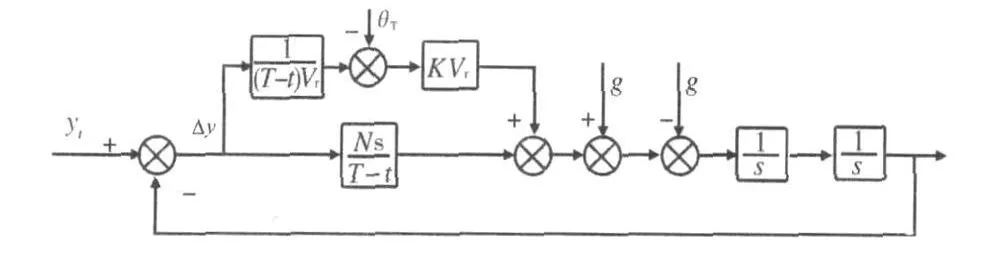
圖3 落角補償制導回路數學模型

模型中一正一負兩個g項分別為重力補償項和重力影響,由數學模型可知,導引律形式為:

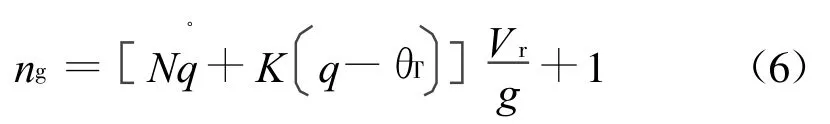
式中:N為比例導引導航比;K為落角補償系數,合理設計這二者的值,可得到滿足約束條件的導引律。

2 導彈性能約束下的大落角攻擊導引律設計

2.1 導彈性能與技術要求

導彈性能與技術要求如表1所示,導彈可用過載與速度的關系如表2所示,其中導彈落角可用彈道傾角近似。

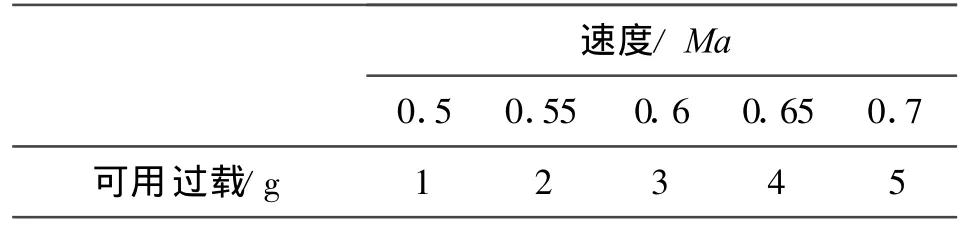
表2 導彈可用過載與速度的關系

2.2 導引律設計

2.2.1 框架角門限+比例導引

框架角門限+比例導引制導方案下,導引律的設計主要是框架角門限值和平飛彈道高度的選取。

框架角門限值可根據式(5)計算,由技術要求可知,導彈落角絕對值要求不小于60°,不考慮平飛俯仰角,計算可得框架角門限值為30°。

平飛彈道高度的選取與過載相關,根據式(1)～式(4)計算得不同過載條件下需求的彈道條件如表3所示。

由導彈性能可知,最大可用過載為5g,導引頭工作高度不大于1km,理論上表 3中需用過載3.5～5g的情況均可實現,但在式(1)～式(4)計算所得為極限轉彎情況,未考慮脫靶量。一般情況下,需用過載越小的越利于保證制導精度,因此,末制導前導彈平飛高度選900m(考慮 100m的平飛高度誤差)。

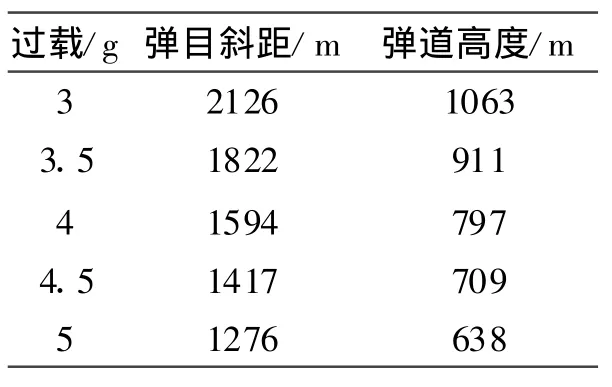
表3 不同式過載條件下的彈道條件

2.2.2 帶過重力補償的比例導引

[1]中詳細介紹了過重力補償比例導引律參數設計方法,文獻指出,重補系數c越大,導航比N越小,導彈落角增量就越大,但彈道末端法向需用過載也越大,在可用過載有限的情況下,可能導致脫靶增大。

導彈最大可用過載為5g,通常情況下采用過重力補償將彈道上拉時,導彈速度會減小,相應的可用過載減小,典型過重力補償末制導彈道速度曲線見圖4。

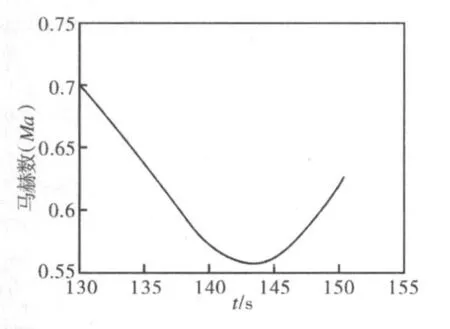
圖4 典型過重力補償末制導彈道速度曲線

可見,在末制導后段,導彈速度較小,可用過載小,因此,過載配置時應將需用過載盡量配置在末制導前段,即導航比應取較大值。但導航比過大會使落角增量偏小,可見,導航比的選擇是關鍵。可采用試算法對導航比3～5、不同重補系數的末制導質點彈道進行試算,結果如表4所示。

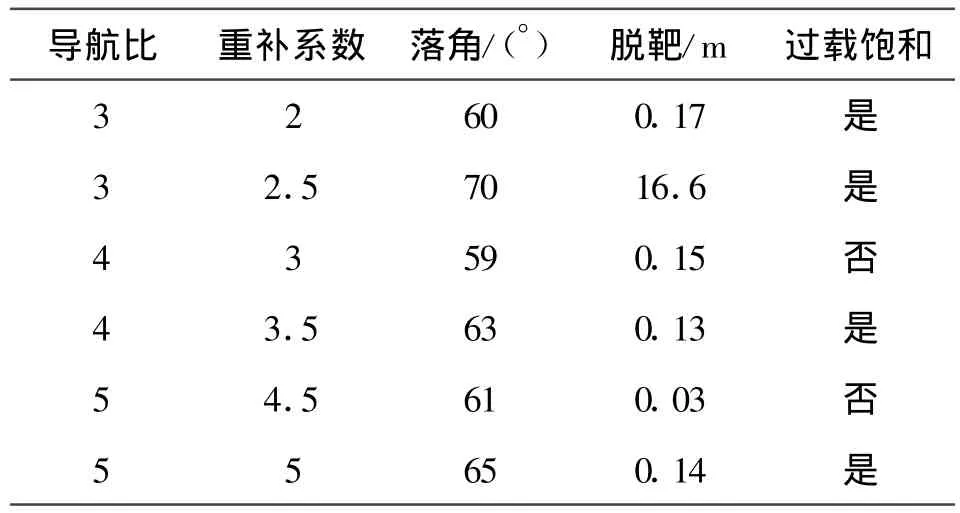
表4 不同參數下的落角與脫靶

由表4結果可知,導航比取5、重補系數取4.5時,落角滿足指標要求,脫靶小,過載未飽和,是較理想的參數配置。

2.2.3 帶落角補償的比例導引

帶落角補償的比例導引律設計與帶過重力補償的導引律設計方法類似,主要是落角補償系數K和導航比N的合理配置。為將需用過載配置在末制導前段,可選取較大的導航比,在導航比選定的基礎上,合理配置K值,使視線角收斂于落角,即可實現導彈以要求的落角進行攻擊。

但應注意,落角補償項隨著視線角逐漸收斂至落角,補償項也逐漸減小,必然導致末制導前段彈道爬升較大而后半段需以大過載下壓,因此,前半段彈道高度有可能超出導引頭工作高度,后半段需用過載超出可用過載范圍。可見,K值最好分段配置,末制導前半段取較小值,延緩彈道爬升,后半段取較大值,延緩彈道下壓。在導航比取5的情況下,K值配置如表5所示。2.2.4 仿真對比分析

表5 落角補償系數設計值

導彈中制導段平飛高度取600m,末制導距離4km,對三種導引律下的末制導彈道進行對比仿真,結果見圖5。

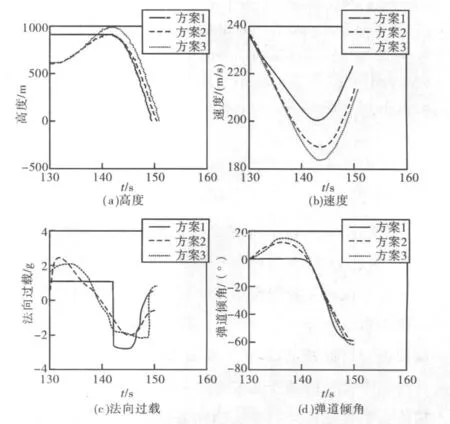
圖5 不同導引律下的末制導彈道

圖中方案1為框架角門限+比例導引,方案2為帶過重力補償的比例導引,方案3為帶落角補償的比例導引,由仿真結果可知:

a)方案1、2的最大彈道高度相近,均比方案3的小,對保證彈道高度在導引頭工作高度1km以下較為有利;

b)方案2、3末速相近,均比方案 1小,可見,方案1對目標的毀傷效果最佳;

c)方案1、3均有過載飽和,飽和后有 3～5s的制導剩余時間,可見,如果末制導控制剛度大于0.5s,則將導致較大脫靶。

3 結論

經過對三種不同大落角攻擊制導方案的設計及仿真對比分析,得出以下結論:

1)框架角門限+比例導引的制導方案彈道高度可提前預知,攻擊末速最大,因此,在可用過載足夠的情況下有利于提高對目標的穿甲能力,但末制導時間短,對導彈快速響應性要求相對較高;

2)帶過重力補償的比例導引方案需用過載最小,在導彈可用過載較小的情況下,有利于減小因過載飽和造成的脫靶;

3)帶落角補償的比例導引方案需用過載大,彈道高度高,對導彈機動能力和導引頭性能要求較高,對小型電視制導空地彈的適用性相對較差。

參考文獻:

[1]林德福,祁載康,夏群力.帶過重力補償的比例導引制導律參數設計與辨識[J].系統仿真學報,2006,18(10):2753-2756.

[2]上官垠黎.圖像尋的制導系統導引規律改進研究[J].兵工學報,2004,25(5):551-555.

[3]孫明瑋,陳志剛.指定傾角的小視場角攻擊導引技術[J].戰術導彈控制技術,2006(4):30-33.

[4]Kim M,Grider K V.Teminal guidance for impact attitude angle constrained flighttrajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.

[5]B S Kiim,J G Lee,H S Han.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[6]P Garnell.Guided weapon control systems[M].Qi Zaikang,Xia Qunli,Beijing:Bejing Institute of Technology,2003.