一道解析幾何題引發的思考

● ●

(應城市第一中學 湖北應城 432400) (應城市第三中學 湖北應城 432400)

一道解析幾何題引發的思考

●陶治國●江斌

(應城市第一中學 湖北應城 432400) (應城市第三中學 湖北應城 432400)

(1)判斷直線l與橢圓E交點的個數；

(2)直線l0過點P與直線l垂直，點M(-1，0)關于直線l0的對稱點為N，直線PN恒過一定點G，求點G的坐標.

這是湖北省部分重點中學2011屆高三第2次聯考的一道解析幾何試題.第(1)小題主要考查了直線與橢圓的位置關系問題;第(2)小題考查了點關于直線對稱以及直線過定點問題.從參考答案來看計算量非常大，學生在單位時間內解出來的人數少之又少.那么命題者到底想考查什么？以下為命題者所給的參考答案：

解(1)由

消去y并整理得

從而

于是

故直線l與橢圓E只有一個交點.

(2)直線l0的方程為

x0(y-y0)=2y0(x-x0),

即

2y0x-x0y-x0y0=0.

設點M(-1，0)關于直線l0的對稱點N的坐標為N(m,n),則

解得

從而直線PN的斜率為

因此直線PN的方程為

即

故直線PN恒過定點G(1,0).

1 筆者的思考

看到題目最常規的思路是:第(1)小題將直線方程和橢圓方程聯立，然后利用判別式來判斷它們的交點個數；第(2)小題利用對稱性求出點N的坐標,然后利用兩點式求出PN所在的直線方程，再判斷直線過哪一個定點.按此方法計算量很大.以上解答為命題人所給的參考答案，非常復雜.筆者在講解試卷之前，想到了如下的簡單方法，僅供讀者參考：

圖1

x′2+y′2=1,

(2)方法1設l0與MN交于點R，先猜定點為G(1,0),再證∠MPR=∠GPR.不妨設y0>0，則

從而

于是

tan∠GPR=tan∠MPR,

即

∠GPR=∠MPR，

則點N在直線PG上,故直線PN恒過定點G(1,0).

方法2設l0與MN交于點R，先猜定點為G(1,0),再證PR平分∠MPG.由

得

從而

又l0的方向向量為(x0,2y0)，故PR平分∠MPG.

2 意外的收獲

待解到此處時，本該結束了，但有學生提出問題：定點是怎樣想到的？對于考生而言,這確實是個難點，這個問題涉及到閱讀材料中的圓錐曲線的光學性質，首先補充一下圓錐曲線的光學性質.

橢圓從橢圓的一個焦點發出的光線，經過橢圓反射后，反射光線交于橢圓的另一個焦點.

雙曲線從雙曲線的一個焦點發出的光線，經過雙曲線反射后，反射光線的反向延長線交于雙曲線的另一個焦點.

拋物線從焦點發出的光線，經過拋物線發射后，反射光線平行于拋物線的軸.

此題可以利用上面的光學性質猜測這個定點：如圖1所示,因為M(-1，0)是橢圓的左焦點，由第(1)小題知l為橢圓的切線，即把MP看作是從橢圓的左焦點發出的一條光線，而點N是點M關于l0的對稱點，則PN就是入射光線MP的反射光線，故反射光線PN必過另一個焦點(1,0).因此可以猜想直線PN恒過定點(1,0).

3 考題鏈接

圖2

關于圓錐曲線光學性質的考查，筆者專門找了幾道相關例題以饗讀者：

例1已知拋物線y2=2px(p>0)的焦點為F，過拋物線上點P(x0,y0)的切線為l,過點P作平行于x軸的直線m,過焦點F作平行于l的直線交m于點M，則|PM|的長為

( )

解如圖2,由拋物線的光學性質可知：∠1=∠2.又由

∠1=∠PFM,∠2=∠PMF,

得

∠PFM=∠PMF，

從而

PF=PM，

因此

( )

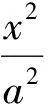
解法1如圖3所示，直線y=x與橢圓的另一個交點為P′，連結P′F,P′F′,PF′.由圓錐曲線的光學性質可知：∠1=∠2.又因為

∠PMN=∠1,∠PNM=∠2,

所以

∠PMN=∠PNM且∠PMN=∠F′EN,

于是

∠PNM=∠F′EN,

從而

PM=PN,F′E=F′N=MF,

PF+PF′=PM+PN=2PM=2a,

即

PM=a,

故選B．

圖3

圖4

解法2如圖4,過點O作OM∥l,F1A∥l,得

OM∥F1A.

由O為FF1的中點,可得

AM=MF,

又∠1=∠PAF1,∠2=∠PF1A,由橢圓的光學性質可知

∠1=∠2,

所以

∠PAF1=∠PF1A，

即PA=PF1.又由橢圓的定義知

PF+PF1=PA+AF+PA=2PA+2AM=

2PM=2a,

即

PM=a.

圖5

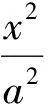
解如圖5所示，過點F1作F1A∥OB,O為F1F2中點且OB∥AF1，易知OB為△AF1F2中位線，于是AB=BF2.由雙曲線的光學性質可知PF1=PA,因此

PA-PF2=PF1-PF=2a,

即

(PB+AB)-(BF2-BP)=2a,

從而

(AB-BF2)+2BP=2a,

得

BP=a,

故

PM=PB=a.