利用“方差”解競賽題

●

(棗莊市第十八中學 山東棗莊 277200)

利用“方差”解競賽題

●李耀文

(棗莊市第十八中學 山東棗莊 277200)

方差公式在解數(shù)學題中有著極其廣泛的應(yīng)用.但是有時也會造成一種錯覺，好像方差公式僅僅是在統(tǒng)計初步內(nèi)容中才使用.實則不然，下面筆者就方差公式在解競賽題中的用武之地舉例如下，供賞析參考.

1 方差公式

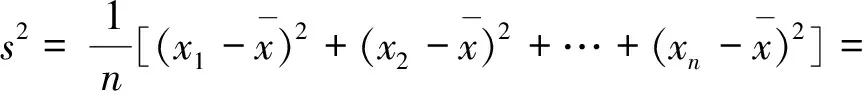
顯然，s2≥0，當且僅當x1=x2=…=xn時，s2=0.

2 應(yīng)用舉例

2.1 求代數(shù)式的值

例1已知實數(shù)x,y,z滿足x+y=5及z2=xy+y-9，則x+2y+3z=________.

(2002年山東省初中數(shù)學競賽試題)

解由x+y=5,可得

x2+y2=25-2xy.

又

z2=xy+y-9,

因此

xy=z2-y+9,

則x+y-1=4,x2+(y-1)2=8-2z2.

視x,y-1為一組數(shù)據(jù)，則由方差公式得

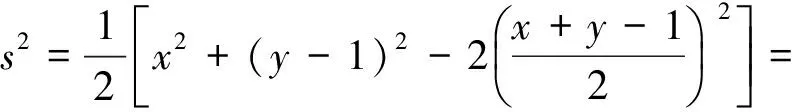
由s2≥0，知-z2≥0，于是z=0，即s2=0.從而x=y-1，解得

x=2，y=3，

所以

x+2y+3z=8.

例2已知實數(shù)x,y,z滿足x=6-3y和x+3y-2xy+2z2=0，求x2y+z的值.

(1998年上海市“鵬欣杯”初中數(shù)學競賽試題)

解由x=6-3y,可得x+3y=6,因此

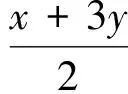
于是

x2+(3y)2=36-6xy=18-6z2.

視x,3y為一組數(shù)據(jù)，則由方差公式，得

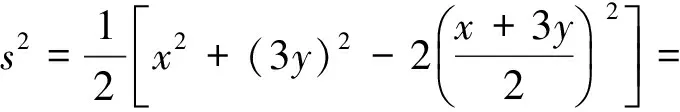
由s2≥0，知z=0，即s2=0.從而x=3y，于是x=3,y=1,所以x2y+z=33×1+0=9.

2.2 求取值范圍

例3已知實數(shù)a,b滿足a2+ab+b2=1，且t=ab-a2-b2，那么t的取值范圍是________.

(2001年全國初中數(shù)學競賽試題)

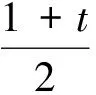
(a+b)2=(a2-ab+b2)+3ab=

可知

t≥-3.

視a,b為一組數(shù)據(jù)，則由方差公式得

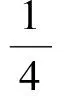
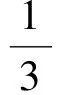
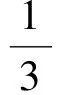
例4實數(shù)a,b,c滿足a2-bc-6a+1=0，b2+c2+bc-2a-1=0，求a的取值范圍.

(1991年湖北黃岡地區(qū)初中數(shù)學競賽試題)

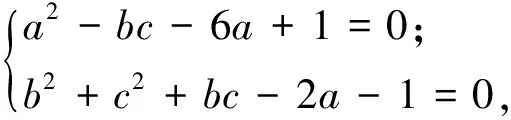
視b,c為一組數(shù)據(jù)，則由方差公式得

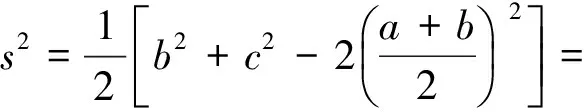
由于s2≥0，因此

3a2-20a+2≤0，

解得

2.3 證明等式或不等式

例5已知實數(shù)a,b,c滿足a=6-b，c2=ab-9.求證：a=b.

證明由a=6-b，c2=ab-9，知

a2+b2=(a+b)2-2ab=18-2c2.

視a,b為一組數(shù)據(jù)，則由方差公式得

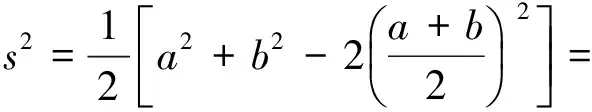
由s2≥0，可知c=0，即s2=0，所以a=b.

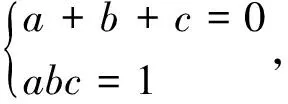
(1991年“曙光杯”初中數(shù)學競賽試題)

證明由a+b=-c得

a2+b2=c2-2ab，

由abc=1得

因此

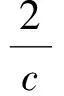
視a,b為一組數(shù)據(jù)，則由方差公式得

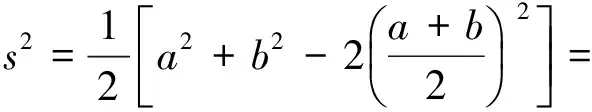
化簡得c3≥4，所以

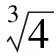
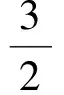
2.4 解方程

例7已知a,b,c滿足方程組

試求方程bx2+cx-a=0的根.

(2001年全國初中數(shù)學聯(lián)賽試題)

因此

a2+b2=(a+b)2-2ab=

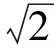
視a,b為一組數(shù)據(jù)，則由方差公式得

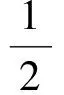
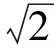
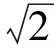
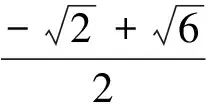
例8解方程:

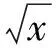
x=a2,y=b2+1,z=c2+2.

原方程可化為

4(a+b+c)=a2+b2+c2+12，

則

a2+b2+c2=4(a+b+c)-12.

視a,b,c為一組數(shù)據(jù)，則由方差公式得

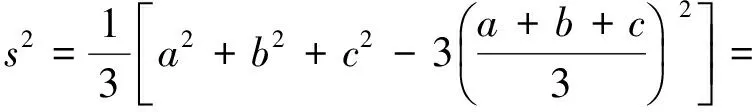
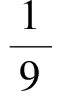
由s2≥0，可知a+b+c=6，于是s2=0，從而

a=b=c=2,

所以

x=4,y=5,z=6.

經(jīng)檢驗,x=4,y=5,z=6是原方程的根.

2.5 解方程組

例9解方程組：

(2008年廣東省廣寧市初中數(shù)學競賽試題)

解視x,y,z為一組數(shù)據(jù)，則由方差公式得

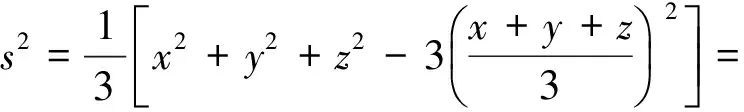
(x-1)2+(y-1)2+(z-1)2=ns2=0,

所以

x-1=0，y-1=0,z-1=0,

從而

x=1,y=1,z=1,

顯然它們滿足方程組中的3個方程.故原方程組的解為x=1,y=1,z=1.

例10解關(guān)于實數(shù)的x,y,z方程組：

(2007年山東省泰安市初中數(shù)學競賽試題)

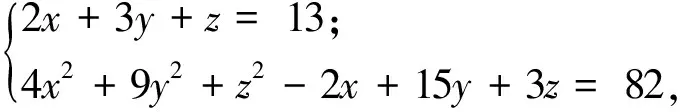
可得

2x+(3y+3)=13-z,

因此

(2x)2+(3y+3)2=104-4z-z2.

視2x,3y+3為一組數(shù)據(jù)，則由方差公式得

由s2≥0，可知z=4，于是s2=0，從而

2x=3y+3,

所以

x=3,y=1.

故原方程組的實數(shù)解為x=3,y=1,z=4.

2.6 求最值

例11已知a,b為實數(shù)，且a2+ab+b2=3，若a2-ab+b2的最大值是m，最小值是n，求m+n的值.

(2008年天津市初中數(shù)學競賽初賽試題)

解設(shè)a2-ab+b2=t，且a2+ab+b2=3，則

于是

(a+b)2=(a2-ab+b2)+3ab=

解得t≤9.視a,b為一組數(shù)據(jù)，則由方差公式得

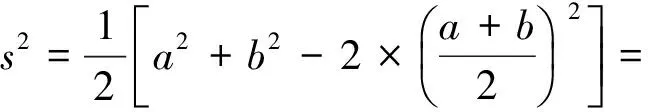
于是t≥1，故1≤t≤9.從而a2-ab+b2的最大值是m=9，最小值是n=1，所以m+n=10.

例12實數(shù)x,y,z滿足x+y+z=5,xy+yz+zx=3，則z的最大值是________.

(2004年“信利杯”全國初中數(shù)學競賽試題)

解由x+y+z=5，xy+yz+zx=3可得

x+y=5-z,

因此

x2+y2=(x+y)2-2xy=-z2+19.

視x,y為一組數(shù)據(jù)，則由方差公式得

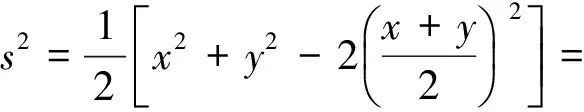
由s2≥0，可知

3z2-10z-13≤0，

解得

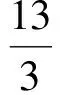
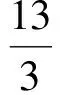
綜上所述，利用方差公式解題，其關(guān)鍵是根據(jù)題設(shè)條件，構(gòu)造出一組數(shù)據(jù)，再運用方差公式

建立等式，結(jié)合s2≥0,通過運算簡化得出s2=0，并借助非負數(shù)性質(zhì)即可解決問題.這種利用方差解題的思路方法，有利于啟迪思維、開拓視野、提高綜合運用知識的解題能力，應(yīng)予以重視.