以美啟真巧解題

●

(桂林師范高等專科學校數學與計算機科學系 廣西桂林 541002)

以美啟真巧解題

●羅奇

(桂林師范高等專科學校數學與計算機科學系 廣西桂林 541002)

美是客觀世界的一種自然屬性，數學作為描述客觀世界的工具當然也具有美的屬性．正如英國數學家羅素(Russell,1872-1970年)所說“數學,如果正確地看,不但擁有真理,而且具有至高的美”.數學美的內容是多方面的,總的來說,數學美的表現常具有簡潔與秩序、對稱與平衡、統一與協調、奇異與極端等特征．并且數學美的這4個方面內容相互聯系、相互滲透，它們構成了和諧與奇妙的數學世界.

數學美在數學解題中具有邏輯思維無法代替的作用，它統領著解題的思想方法，啟迪著解題的直覺思維，往往能夠引領我們找到解題的方向和途徑，那么如何利用數學美來指導解題呢?這就要求我們在分析和處理問題時有意識地用數學美的特征去考察和感悟數學對象,思考和轉化數學問題,進而培養對數學的美感．下面通過幾個例題來欣賞如何利用數學美指導解題．

1 以簡馭繁、變亂為序，追求簡潔與秩序美

簡潔、清晰、秩序、明快,會給人以美感．數學以高度抽象、極其簡潔的形式和思想反映客觀世界.在雜亂無章的客觀現象中,抽象出秩序井然的數學理論,又用簡單、有序的數學形式來表達、解釋并處理更多的客觀事物和現象,這就是數學的簡潔與秩序美．

許多的數學問題,雖然其表現形式可能較為復雜和無序,但其本質總是存在簡單和秩序的一面．這就要求我們在處理問題時盡可能用簡潔與秩序的觀點和方法對數學問題進行轉化，從問題的各個方面選擇新信息,并有效地對已知信息進行組合、編碼以獲得最佳解題方案．譬如利用未知、已知換位處理，往往能夠化難為易．

例1已知a∈[0,1]，解關于x的不等式:

(a-1)lg2x-9algx+2a+1>0.

分析一般地,將不等式看成是關于lgx的二次不等式，利用換元法求解，但整個過程較繁雜.注意到在不等式中a的最高次數是1，相對x更為簡單.若把x作為已知,把a作為變量,則可將原不等式化為關于a的一元一次不等式,并按a的降冪順序排列得

f(a)=(lg2x-9lgx+2)a-lg2x+1>0,

化簡得

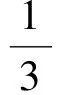
即

同樣利用變換、構造、排序等轉化的策略,也能夠獲得解題的突破口．

例2求由1,2,3,…,n這n個數組成的允許重復的m個數的數組的組數．

分析在1,2,3,…,n中任取一個允許重復的m個數組成的數組集合為

A={(a1,a2,…,am)|1≤a1,a2,…,am≤n},

所求的組數就是集合A的元素個數.從簡潔與秩序美的觀點考慮，將A中的數組從小到大排序,得到集合B={(b1,b2,…,bm)|1≤b1≤b2≤…≤bm≤n,bj=ai(1≤i≤m,1≤j≤m)},集合B的元素仍然是有重復數的數組.為了更為簡潔，構造一個沒有重復數的數組集合C，使從集合B到集合C之間建立一個雙射f，為此將b1,b2,…,bm從第1個開始分別加上0,1,2,…,m-1得到m個數c1,c2，…,cm,這樣得到集合

C={(c1,c2,…,cm)|1≤c1

2 左右均衡、前后照應，聯想對稱與平衡美

德國數學家魏爾斯特拉斯指出“美和對稱性緊密相連”．數學中的對稱與平衡美不單指形象的幾何圖形對稱,也包括抽象的關系、地位、形式、方法等的對稱與平衡．

對稱與平衡美是數學美的重要特征之一,在數學解題中,我們應充分利用數學知識、方法、形式或圖形的對稱與平衡性求解.一方面,具有相同結構特征的數式具有同等的地位和相同的處理手法,另一方面,數式結構的對稱也蘊含著解法的對稱．

例3已知四面體V-ABC的6條棱長之和為l，且∠AVB=∠BVC=∠CVA=90°，求它體積的最大值．

分析設VA=a，VB=b,VC=c,則

因此

(1)

而V-ABC的體積為

(2)

于是問題轉化為在式(1)的條件下，求式(2)的最大值.觀察式(1)和式(2)知，a,b,c地位對等，可以從對稱與平衡的原則出發，提出猜想：由對稱性，是否當a=b=c時體積最大呢？此時

從而

因此只要證明

即證

而上式是成立的，因為

對偶關系也可視為對稱與平衡的一種形式．在解題中,如何“配對”以及應“配”些什么,都應在對稱與平衡美的引導下進行．

分析注意到

將上述兩配對式相乘得

因為

72n+1=7(50-1)n=7[5p+(-1)n]=

35p+7(-1)n=

35q+2(-1)n(p,q∈Z)，

3 化分歧為一致、變混亂為協調，利用統一與和諧美

數學作為研究客觀世界的數量關系和空間形式的科學,它反映了客觀世界的統一與和諧．數學的統一與和諧美是指數學各分支之間、分支內部及分支與整體之間互相貫通、和諧和互相轉化．

統一與和諧美也是促使解題成功的重要因素之一，數學除了在形式上追求統一與和諧之外,在結論、方法上也追求統一與和諧．

可見利用圓錐曲線的統一方程,不僅很容易地證明了結論,而且還推廣了結論!

我們也常常通過變換已知與未知的數、式、形,使它們消除差異而達到統一與和諧的形式來啟迪解題思路、發現解題規律．

sinB<3(sinC-sinA),

這樣就實現了與已知條件相對統一和諧．但還不夠,不等式中有3個角，能否把它們化為同角的三角函數呢?考慮到3A+B=π，則C=2A，于是

sin3A<3(sin2A-sinA).

再把倍角統一成單角,得

3sinA-4sin3A<3(2sinAcosA-sinA)，

由sinA>0得

3-4sin2A<3(2cosA-1)，

再把不同名的三角函數統一為同名的三角函數,

2cos2A-3cosA+1<0，

即

(2cosA-1)(cosA-1)<0.

4 標新立異、探討極致，揭秘奇異與極端美

奇異與極端也是一種美,正如英國哲學家培根所說“沒有一個極美的東西不是在調和中有著某些奇異”,我國著名數學家徐利治教授也指出“奇異是一種美,奇異到極度更是一種美”.數學的奇異與極端美,是指數學中的統一與和諧或對稱與平衡在一定條件下的破壞，是數學中的新思想、新理論、新方法對原有的習慣法則和格局的突破.

一些出人意料的想法往往是極端的設想,但常能使問題豁然開朗．譬如運用特殊化方法探討幾何圖形的極端位置，就體現了數學的奇異與極端美．

例7一圓與直線3x+4y+5=0相切于點(1,-2),且經過點(4,7),求圓的方程．

分析切點(1，-2)可以看成半徑為0的圓，直線3x+4y+5=0可看成通過該圓的直線，基于這種奇異和極端的想法，此題可以跳出設圓方程的一般方法,用曲線系方程來求解,則更為簡捷．

首先過切點(1，-2)的方程為(x-1)2+(y+2)2=0，通過直線3x+4y+5=0和該點圓的圓系方程為

(x-1)2+(y+2)2+t(2x+4y+5)=0,

代入點(4,7)的坐標,求得t=-2,故所求圓的方程為

(x-1)2+(y+2)2-2(3x+4y+5)=0，

即

x2+y2-8x-4y-5=0.

對于某些數學問題,若能抓住其“個性特點”,打破問題求解的習慣法則，尋找它與其他知識的聯系,則往往能找到出人意料的新奇解法和出人意料的結果．

分析本題若利用三角公式進行化簡求值，需要利用和差化積和倍角公式以及恒等變形的化簡技巧，過程比較復雜．那么是否可以利用所給式子是余弦函數的代數和以及余弦函數積化和差后仍然是余弦函數的代數和的個性特點求解?

解得

同樣地，借助統一與和諧美的思想將原式的運算符號統一，可以得到：

聯想復數與三角之間的關系，可將三角問題化歸為復數問題求解.如果觀察到各個角度的倍數關系，那么還可以構造幾何圖形或者向量求解……如此新奇的解法無不體現了數學知識的和諧與奇異.

可見數學問題的求解需要數學美的引領，并且也應該以美啟真去追求那些漂亮的解法，這樣在我們心靈深處就會引起一種愉快的體會和欣賞.通過如此長期的訓練,我們就能透過抽象的數學符號看到美的形象，透過嚴密的邏輯推演領略美的神韻，就可以完善人的思維品質、陶冶人的情趣、增強人的創造能力.