幾乎處處收斂、近一致收斂和依測度收斂之間的等價(jià)條件研究

續(xù)小磊 (寧夏大學(xué)數(shù)學(xué)計(jì)算機(jī)學(xué)院,寧夏 銀川 750021)

續(xù)曉欣 (中北大學(xué)理學(xué)院數(shù)學(xué)系，山西 太原 030051)

幾乎處處收斂、近一致收斂和依測度收斂之間的等價(jià)條件研究

續(xù)小磊 (寧夏大學(xué)數(shù)學(xué)計(jì)算機(jī)學(xué)院,寧夏 銀川 750021)

續(xù)曉欣 (中北大學(xué)理學(xué)院數(shù)學(xué)系，山西 太原 030051)

研究了函數(shù)列的近一致收斂、幾乎處處收斂和依測度收斂之間的關(guān)系，在此基礎(chǔ)上給出了它們之間彼此等價(jià)的充分必要條件。

測度；可測集；可測函數(shù)列；幾乎處處收斂；近一致收斂；依測度收斂

可測函數(shù)序列的收斂性有很多種，如幾乎處處收斂、依測度收斂、依概率收斂、完全收斂、一致收斂、幾乎一致收斂、近一致收斂、平均收斂、強(qiáng)收斂和弱收斂等。如此多收斂之間的強(qiáng)弱關(guān)系引起了許多測度論學(xué)者們的關(guān)注[1-6]。其中，幾個(gè)經(jīng)典定理，如Egoroff (逆)定理、Lebesgue定理、Riesz定理在測度有限的前提下對幾乎處處收斂、近一致收斂和依測度收斂做了最基本研究：一致收斂是很強(qiáng)的收斂，在一般情況下很難實(shí)現(xiàn)，因而應(yīng)用大受限制，而處處收斂和幾乎處處收斂的條件相對弱一些。

下面，筆者研究了測度有限可測集上幾乎處處有限的可測函數(shù)列和一般可測集上的幾乎處處有限的單調(diào)可測函數(shù)列幾乎處處收斂、近一致收斂和依測度收斂3種收斂之間的等價(jià)條件。

1 基本概念

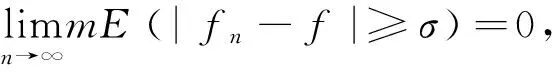
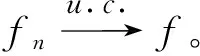
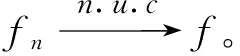
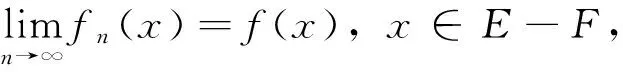
引理1[1]設(shè)f和{fn}n≥1都是E上幾乎處處有限的可測函數(shù)，則：

i){fn}n≥1在E上幾乎處處收斂于f,當(dāng)且僅當(dāng)對任意的ε>0，有：

ii){fn}n≥1在E上近一致收斂于f,當(dāng)且僅當(dāng)對任意的ε>0，有：

引理4[6]設(shè)f和{fn}n≥1都是E上幾乎處處有限的可測函數(shù)，若{fn}n≥1在E上近一致收斂于f，則{fn}n≥1在E上依測度收斂于f。

引理5[7-9](勒貝格Lebesgue定理) 設(shè)f和{fn}n≥1都是E上幾乎處處有限的可測函數(shù)，若mE<+∞且{fn}n≥1在E上幾乎處處收斂于f，則{fn}n≥1在E上依測度收斂于f。

引理6[7-9](Riesz定理) 設(shè)f和{fn}n≥1都是可測集E上的幾乎處處有限的可E測函數(shù)，若{fn}n≥1在E上依測度收斂于f，則{fn}n≥1存在子列{fnk}k≥1在E上幾乎處處收斂于f。

2 主要結(jié)論

定理1設(shè)f和{fn}n≥1都是E上幾乎處處有限的可測函數(shù)，且{fn}n≥1為E上的單調(diào)函數(shù)列，若{fn}n≥1在E上幾乎處處收斂于f，則{fn}n≥1在E上依測度收斂于f。

證明由{fn}n≥1在E上幾乎處處收斂于f，可得對任意的ε>0，有：

成立，記E0=E(fn(x)→f(x))，對于任意的x0∈E0，則{fn(x0)}n≥1單調(diào)收斂于f(x0)，于是有:

|fn+1(x0)-f(x0)|≤|fn(x0)-f(x0)|

成立。因此，對任意ε>0，E0(|fn+1-f|≥ε)?E0(|fn-f|≥ε)，即E(|fn-f|≥ε)，為單調(diào)遞減集族，于是由測度的性質(zhì)可得：

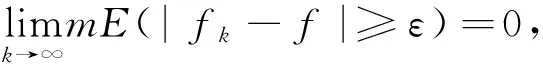
注：在mE<+∞條件下，幾乎處處收斂,近一致收斂和依測度收斂彼此等價(jià)。

引理7設(shè)f和{fn}n≥1都是E上幾乎處處有限的可測函數(shù)，且對于任意x∈E，滿足以下條件之一：

i)f1(x)≤f2(x)≤f3(x)≤……≤fn(x)≤fn+1(x)≤……≤f(x)；

ii)f1(x)≥f2(x)≥f3(x)≥……≥fn(x)≥fn+1(x)≥……≥f(x)，

則E(|fn-f|≥ε)為單調(diào)遞減集族。

證明事實(shí)上，對于任意x∈E，若f和{fn}n≥1滿足以上條件之一，則對于任意n≥1有:

|fn+1(x)-f(x)|≤|fn(x)-f(x)|

于是，對于任意ε>0，由|fn+1(x)-f(x)|≥ε可得|fn(x)-f(x)|≥ε，所以:

E(|fn+1-f|≥ε)?E(|fn-f|≥ε) (n≥1)

成立，即E(|fn-f|≥ε)為單調(diào)遞減集族。

定理2設(shè)f和{fn}n≥1滿足引理7的條件，則在E上{fn}n≥1幾乎處處收斂于f與{fn}n≥1依測度收斂于f彼此等價(jià)。

證明對于任意ε>0，由引理7可知E(|fn-f|≥ε)為單調(diào)遞減集族，則有:

成立，于是由引理1可得幾乎處處收斂與依測度收斂彼此等價(jià)。

定理3設(shè)f和{fn}n≥1滿足引理7的條件，則在E上{fn}n≥1近一致收斂于f與{fn}n≥1依測度收斂于f彼此等價(jià)。

證明對于任意ε>0，由引理7可知E(|fn-f|≥ε)為單調(diào)遞減集族，則有:

成立，于是由引理1可得近一致收斂與依測度收斂彼此等價(jià)。

3 結(jié) 語

主要利用幾乎處處收斂和近一致收斂的等價(jià)刻畫，進(jìn)一步考察了各種收斂之間的強(qiáng)弱關(guān)系，通過對幾種收斂關(guān)系定理的討論和分析，可以看出在幾種收斂關(guān)系中各種前提條件的重要性，幾乎處處收斂、近一致收斂和依測度收斂彼此等價(jià)的條件除了可測集的有界性mE<+∞外，函數(shù)序列的單調(diào)性也可以保證以上3種收斂彼此等價(jià)。由此可見序列的單調(diào)性也是一個(gè)較為重要條件，因此外界條件的改變使得各種強(qiáng)弱不同的收斂得到了統(tǒng)一，進(jìn)一步增強(qiáng)了對可測函數(shù)在理論上的理解和應(yīng)用。

[1]溫華永.葉果洛夫定理的一個(gè)新證明[J].四川師范大學(xué)學(xué)報(bào)，2000，23(6)：576-577.

[2]袁守成.可測函數(shù)序列的完全收斂性[J].株洲師范高等專科學(xué)校學(xué)報(bào)，2007，12(5)：28-29.

[3]張玲.幾種收斂間的關(guān)系[J].高等數(shù)學(xué)研究，2005，8(4)：12-15.

[4]林謙.關(guān)于可測函數(shù)列的各種收斂性[J].云南師范大學(xué)學(xué)報(bào)，1994，14(1)： 8-17.

[5]楊潔.關(guān)于可測函數(shù)列各種收斂性的幾點(diǎn)注記[J].工程數(shù)學(xué)，1998，14(2)： 120-123.

[6]尹敏.可測函數(shù)列的幾種收斂性之間的關(guān)系[J].井岡山師范學(xué)院學(xué)報(bào)， 2001，22(6)：42-44.

[7]程其襄.張奠宙，魏國強(qiáng)，等.實(shí)變函數(shù)與泛函分析基礎(chǔ)[M].第2版.北京：高等教育出版社，2003：205-206.

[8]夏道行.實(shí)變函數(shù)論與泛函分析 [M].第2版.北京：高等教育出版社,1985:185-190.

[9]嚴(yán)加安.測度論講義[M].北京：科學(xué)出版社,2004.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.10.003

O175.1

A

1673-1409(2011)10-0010-02