一類復雜時滯系統的λ實用穩定性

王曉佳

(合肥工業大學數學學院,安徽合肥 230009)

一類復雜時滯系統的λ實用穩定性

王曉佳

(合肥工業大學數學學院,安徽合肥 230009)

主要研究了一類具有多時滯的復雜微分系統的λ實用穩定性問題,通過對Lyapunov函數方法以及比較原理的運用,建立一般形式的實用穩定性直接判據.在此基礎上給出討論這類多時滯復雜微分系統實用穩定性的新方法.

泛函微分方程;λ實用穩定性;時滯

1 引 言

隨著科技發展和人們對諸如控制系統、生態系統、航空系統、經濟系統等領域的研究,人們遇到了大量的時滯現象.在涉及到線性過程的許多應用中,都存在有滯后現象,即事物的發展趨勢不僅依賴于當前的狀態,而且還依賴于事物的過去歷史.在數學上描述這類運動要用時滯泛函微分方程(簡稱時滯系統[1]).由于它本質上是無限維的,這樣就給系統動力學研究帶來許多困難.

對滯后系統,研究歷史雖已有三十年,但穩定性、穩定性理論仍處于初創階段,特別是對于這種類型系統的實用穩定性,據作者所知,研究結果[4-5]并不是很多,而對于這類系統的λ實用穩定性,研究幾乎處于空白.在本文中,我們運用研究運動的實用穩定性的創新方法,來建立時滯系統的實用λ穩定性的充分條件.

考慮下面這個多時滯微分系統

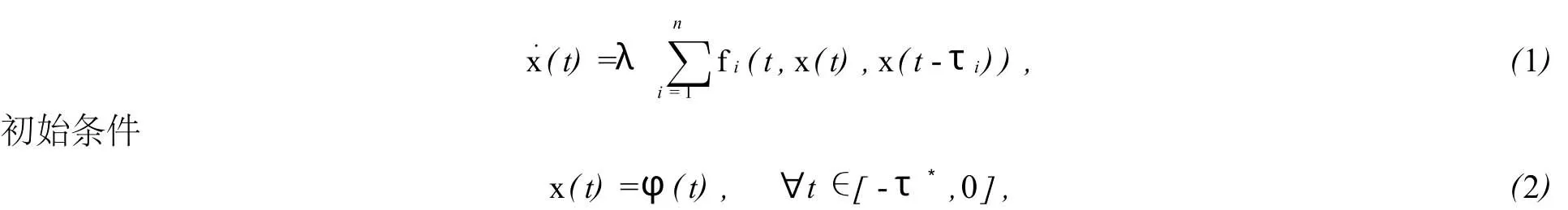
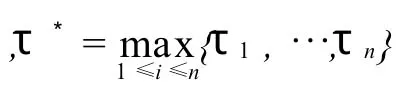
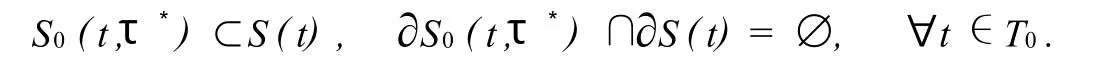
本文約定,?x,y∈Rn,x≤y的充分必要條件為xi≤yi(i=1,2,…,n).下面我們先介紹一些預備知識,然后給出判定此類復雜時滯系統(1)的λ實用穩定性的結論.

2 預備知識

定義1 稱系統(1)是實用λ穩定的,如果對于任何初始函數φ(θ)∈S0(t),τ＊≤θ≤0,存在λ＞0使當0＜λ＜λ0時,對所有的?t0∈T0滿足x(t0,φ,λ)(t)∈intS(t).

假設對于系統(1)存在極限

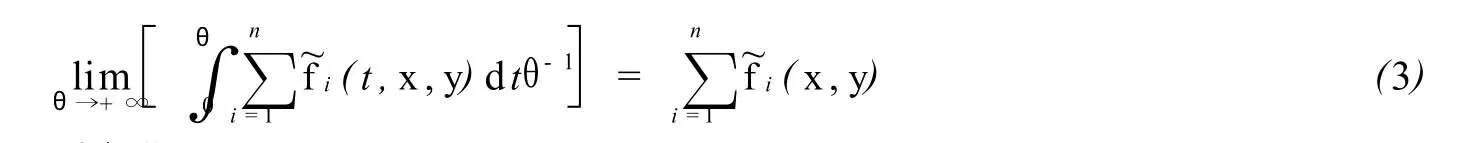
且為關于x∈D1,y∈D2的一致極限.

在區域T0×D1×D2,D1?Rn,D2?Rn內,向量函數由關系式

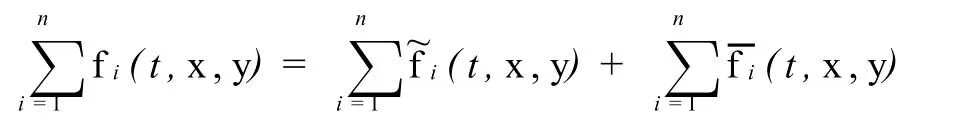
確定,其中ˉfi有零均值.

考慮對應于方程組(1)的均值方程組

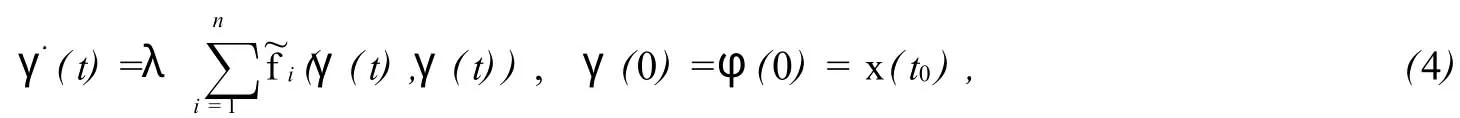
對(4)考慮具有連續且可微的分量的向量函數V∶Rm→Rm+與函數Γ∈C1(R+,Rm),Γ有可微的分量,同時有

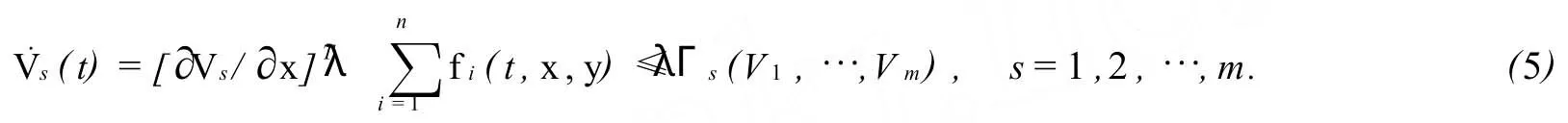
下面,將在對均值方程組(4)的解的性質的某些假設條件下,建立方程(1)的實用λ穩定的條件.由文獻[4],[5]不難得到:

引理1 假設在方程組(1)中的函數fi(t,u,v)(i=1,…,n)在區域Q={(t,u,v)∶t∈R+,u∈D1, v∈D2}內有定義且連續,同時假設在這個區域內成立:

(Ⅰ)存在函數M(t)與常數M0,使得在任何有限區間[t1,t2]?T0上滿足

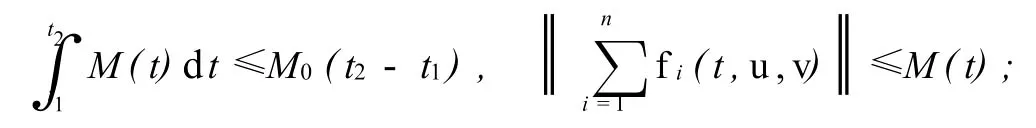
(Ⅱ)存在函數H1(t),H2(t),常數h1,h2與K類函數ψ1,ψ2使得

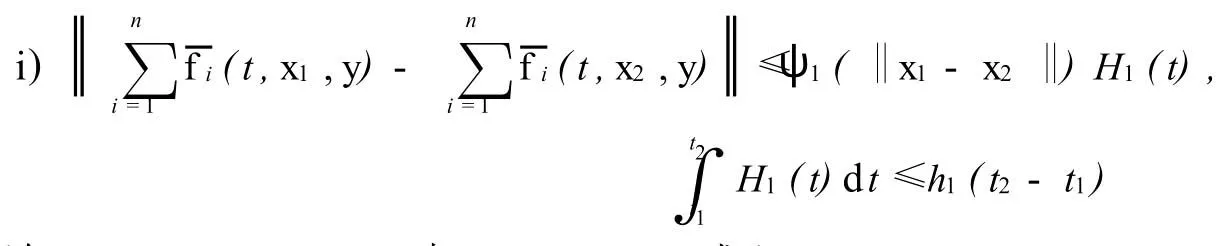
對任何x1,x2∈D1,y∈D2與[t1,t2]?T0成立;

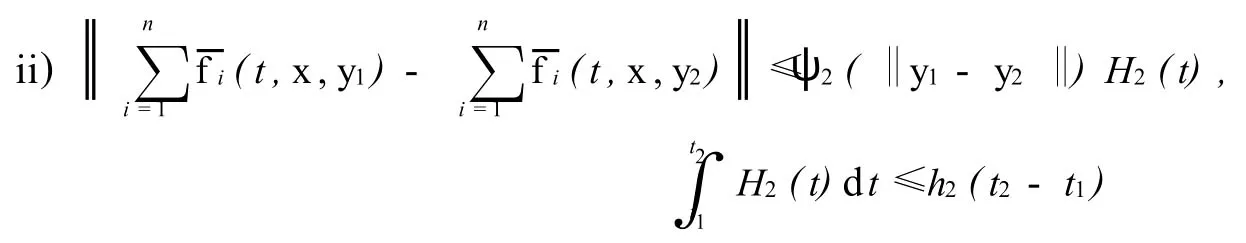
對任何y1,y2∈D2,x∈D1與[t1,t2]?T0成立;

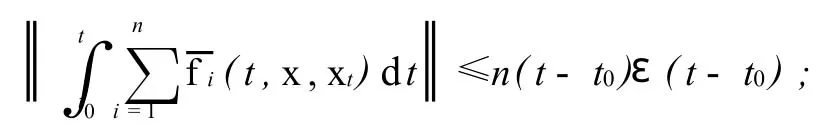
(Ⅳ)x1∈D1,y∈D2一致存在極限式(3),且向量函數?fi(x,y)滿足關于x1∈D1的具有常數N的李普希茲條件,

則對于任何η≥0,L≥0,能找出一個λ0,使當0＜λ＜λ0,在區間0≤t≤Lλ-1上滿足不等式

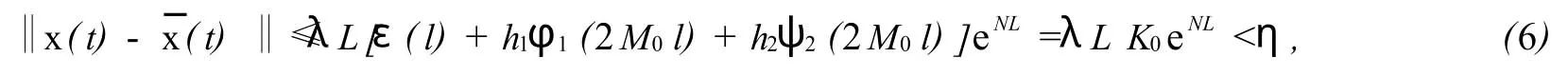
3 主要結果

與不等式組(5)一起來考慮比較方程組

對系統(1),利用引理(1)的估計式與比較原理,可得出系統(1)的實用λ穩定性的充分條件.

定理1 對系統(1),假設

(Ⅰ′)滿足引理1的條件(Ⅰ),(Ⅱ);

(Ⅱ′)存在向量函數:V:Rn→R與函數Γ∈C(R,Rm)滿足不等式(5);

(Ⅲ′)存在可積函數Γ1(t),Γ2(t),常數z1,z2與K類函數ψ1,ψ2使得

[1] 鄭祖庥.泛函微分方程理論[M].合肥：安徽教育出版社,1994.

[2] 蔣威.退化時滯微分系統[M].合肥：安徽大學出版社,1998.

[3] 王曉佳,蔣威.一類中立型方程的漸近穩定性[J].合肥工業大學學報,2007,30(7)：912-914.

[4] Liu Xinzhi.Practical Stabilization of control System with Impulse Effects[J].Journal of Mathematical Analysis and Applications,1992,166：563-576.

[5] Chu Tianguang,Wang Zhaolin.Practical stability and liapunov stability of delay systems[J].Acta Mechanica Sinica,1996,28(2)：200-206.

[6] Wang Xiaojia,Yang Shanlin,Wang Haijiang,etc.Dynamic GM(1,1)Model Based on Cubic Spline for Electricity Consumption Prediction in Smart Grid[J].Chinacommunications,2010,7(4)：83-88.

[7] Wang Xiaojia,Yang Shanlin.On Delay-Dependent Stability for aclass of Neutral Systems[C].2009 The 5th International Conference on Wireless Communications Networking and Mobile Computing.

[8] Wang Xiaojia,Jiang Wei.Stability of Singular Uncertain Differential Systems with Multiple Time Varying Delays [J].Annal of Differential Equations,2009,25(4)：443-452.

[9] 王曉佳,蔣威.退化時滯中立型微分系統的特征根分布與指數穩定[J].應用數學,2010,23(1)：138-144.

[10] 王曉佳.多時滯微分方程數值穩定性[J].應用數學與計算數學學報,2010,24(1)：93-99.

[11] 王曉佳.變時滯的退化滯后型微分系統的穩定性[J].數學的實踐與認識,2010,40(8)：196-201.

[12] 王曉佳.變時滯區間中立型系統的穩定性新判據[J].黑龍江大學自然科學學報,2011,28(1)：34-39.

Theλ-Practical Stability for aclass of Complex Delay Systems

WA N G Xiao-jia
(Hefei University of Technology,Hefei 230009,China)

This paper is devoted to the investigation forλ-Practical Stability for aclass of systems with multiple delays.By using Lyapunov functions and comparison principle,we will get some criteria for delay systems.

functional differential equations;λ-Practical Stability;delay

O175

A

1672-1454(2011)03-0093-05

2008-09-05

國家自然科學基金項目(70631003)