非負矩陣譜半徑的一個新界值

李丹青

(電子科技大學數學科學學院,成都 611731)

非負矩陣譜半徑的一個新界值

李丹青

(電子科技大學數學科學學院,成都 611731)

在Wielandt定理的基礎上進行了推廣,得到了一種估計非負矩陣譜半徑的新方法,數值例子顯示了新方法所得到的結果更為精確.

非負矩陣;譜半徑;界

1 引 言

矩陣A=(aij)∈Rn×n的n個特征值λ1,λ2,…,λn組成的集合稱為A的譜,其中n個特征值的模的最大值稱為A的譜半徑,記為ρ(A).Perron-Frobenius定理中指出,對于n階不可約非負矩陣A,其譜半徑ρ(A)是A的特征值并且A有一個對應于ρ(A)的正特征向量.

非負矩陣譜半徑的估計作為非負矩陣理論的核心問題之一,許多學者都致力于這方面的研究.其中最有名且應用最多的界值由Frobenius首先得到,即非負矩陣A的譜半徑的上下界分別為A的最大行(列)和與最小行(列)和.對于正矩陣A,Lederman,Ostrowski,Brauer對Frobenius界值又相繼作了改進.但對于最大行(列)和與最小行(列)和相差很大的矩陣,上述界值并不理想,因此需要更多更好的方法.

目前關于譜半徑的界已經有許多深刻的結論,其中有如下的著名定理:

定理[1](Wielandt) 設A=(aij)是n階非負矩陣,其譜半徑為ρ(A),x是n維列正向量,那么

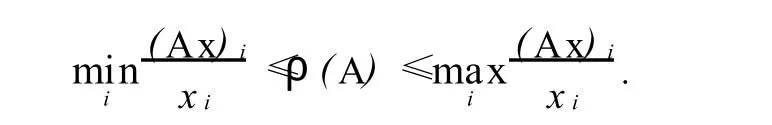
如果A不可約,那么等號成立當且僅當x是相應于ρ(A)的特征向量.

本文將上述定理進行了推廣,通過理論和數值例子的證明,可以顯示推廣后的方法所得到的結果精確度更高.

2 主要結論

引理1[2]設q1,…,qn是正數,p1,…,pn是任意實數,則

當且僅當所有的比值pi/qi相等時,等號成立.

定理1 設A是n階不可約非負矩陣,x是n維列正向量,則對任意的m∈N+,有

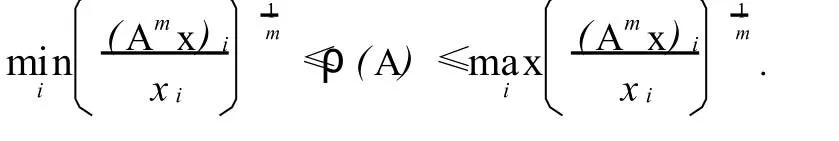
3 數值例子

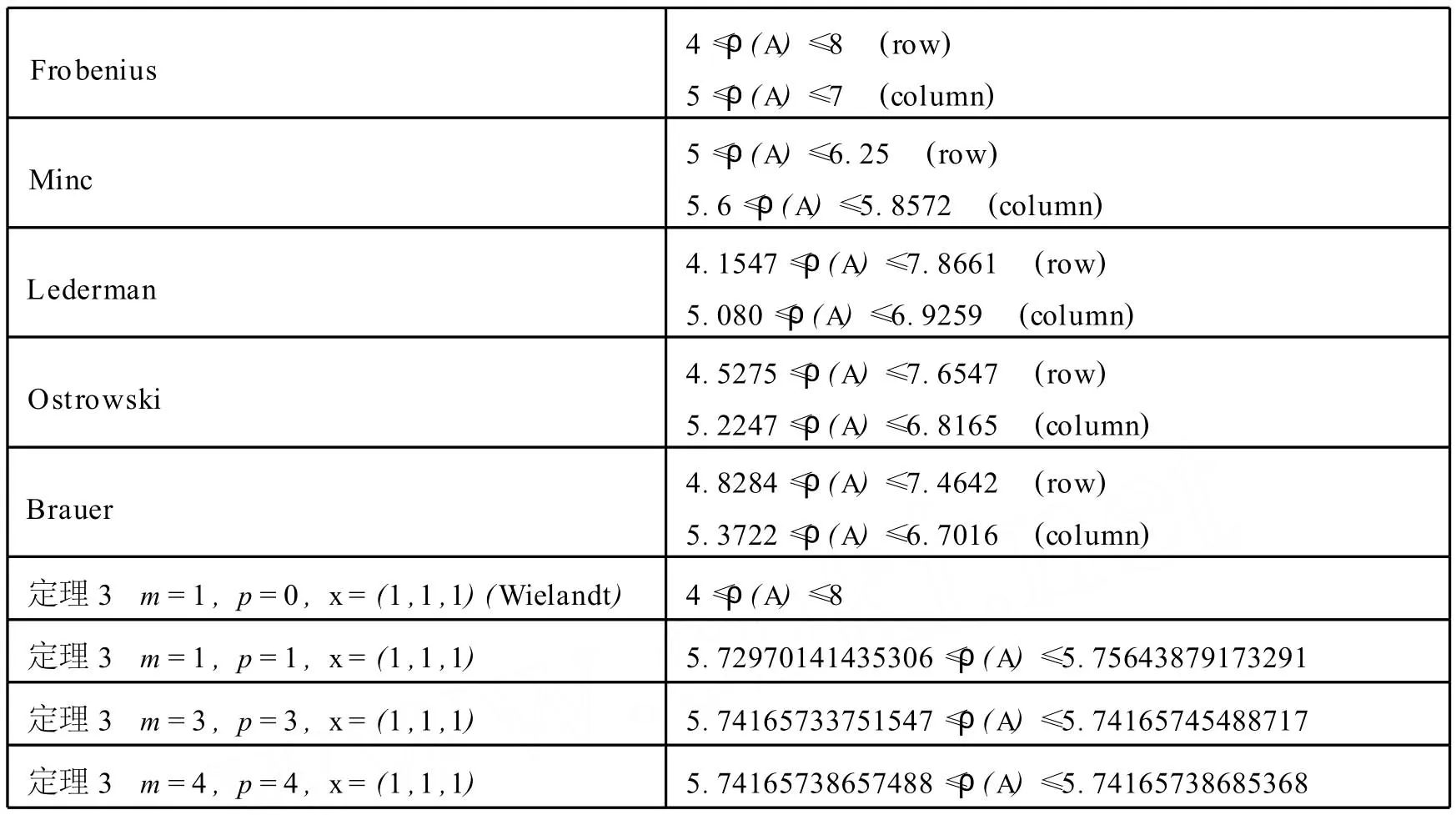
表1 各種界值比較

從上表可以看出,隨著m,p的增加,譜半徑界值更為精確.通過更為多的數值例子可以得出,界值關于p的收斂速度比關于m的收斂速度要快.但本文中并未給出證明.

注 求不可約非負矩陣譜半徑的任何方法都可用以計算一般非負矩陣的譜半徑,本文中的方法也不例外.事實上,對于任意的非負矩陣A(可約或不可約),都存在置換矩陣P使

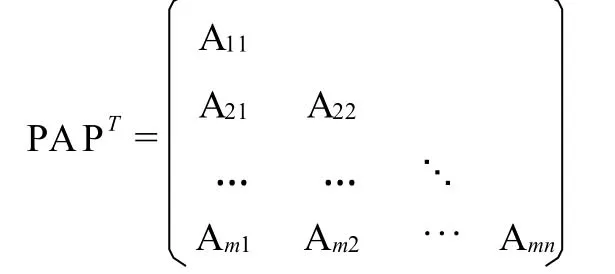
為下三角形分塊矩陣,其中Aii(i=1,…,m)都是不可約非負矩陣,而且ρ(A)=ρ(PAP)T=maxρ(Aii).

致謝 衷心感謝黃廷祝教授的指導.

[1] Berman A and Plemmons R J.Nonnegative matrices in Mathematics Science[M].New York：Academic Press, 1979.

[2] Minc H.Nonnegative Matrices[M].New York：Wiley,1988.

[3] 黃廷祝,楊傳勝.特殊矩陣及應用[M].北京：科學出版社,2007.

[4] 殷劍宏.求非負矩陣最大特征值與特征向量C-W方法[J].合肥工業大學學報,2000,23(5)：752-756.

A New Bound for the Spectral Radius of a Nonnegative Matrix

L I Dan-qing
(School of Appl.Math.,Univ.of Electronic Science and Technology of China,Chengdu,Sichuan 611731,China)

Based on a theorem of Wielandt’s,a new estimate for the spectral radius of a nonnegative matrix is presented.A numerical example is provided to illustrate the effectiveness of this approach.

nonnegative matrix;spectral radius;bound

O151.21

A

1672-1454(2011)03-0026-04

2008-07-01;[修改日期]2009-04-02