一類具有Z2－等變性質(zhì)的平面七次哈密頓向量場(chǎng)的相圖

李艷梅

( 楚雄師范學(xué)院數(shù)學(xué)系，云南楚雄675000)

一類具有Z2－等變性質(zhì)的平面七次哈密頓向量場(chǎng)的相圖

李艷梅

( 楚雄師范學(xué)院數(shù)學(xué)系，云南楚雄675000)

In this paper，by the use of the method of qualitative analysis of differential equations，the phase portraits of a planar septic Hamiltonian vector fields with Z2－equivariant property are given and the parameter space is classified．

Z2－equivariant property;septic Hamiltonian vector field;singular point;phase portrait

In recent decades，the phase portraits of planar quintic Hamiltonian vector fields with equivariant property have been discussed［1～5］，but few papers have discussed the phase portraits of planar septic Hamiltonian vector fields．In this paper，we will classify the phase portraits of following planar septic Hamiltonian vector fields with equivariant property，

where is a parameter with k＞1

1 Properties of the Singular Points

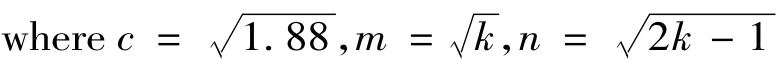
The Jacobian of this system is

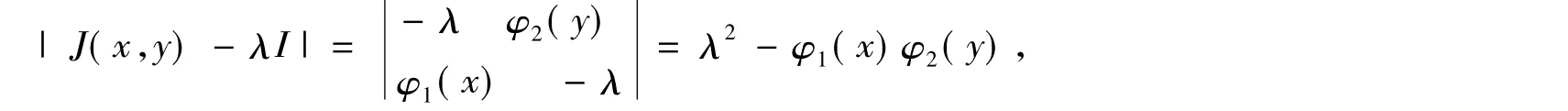
in which

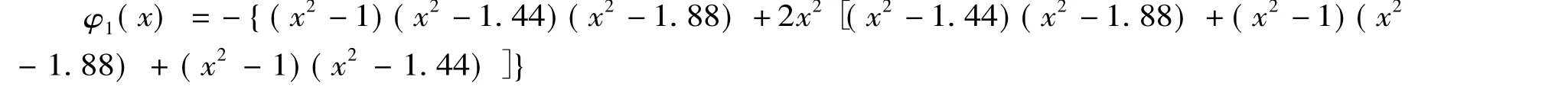
φ2(y) =(y2－1)(y2－k)(y2－2k+1)+2y2［(y2－k)(y2－2k+1)+(y2－1)(y2－2k+1)+(y2－1)(y2－k)］

Discussing the Jacobians of these singular points，we have no difficulty in obtaining the following results:

Theorem 1The singular points(0，0)，( ± 1.2，0)，(0，m)，( ± 1，1)，( ± 1.3，1)，( ± 1.2，m)，( ± 1，n) ，and( ± 1.3，n)are center，and the others are saddle points．

2 Phase Portraits of the System(1)

The Hamiltonian of the system is

H(x，y)=［3x8－17.28x6+36.1632x4－32.4864x2+3y8－12ky6+6(2k2+2k－1)y4－12(2k2－ k)y2］/24

Obviously，the function H(x，y)satisfies the equality H(x，y)=H(x，0)+H(0，y)，and it is not difficult to get

H( ± 1，0)=H(± c，0)= － 0.4418，H(± 1.2，0)= － 0.4371148，

H(0，1)=H(0，n)= － (2k － 1)2/8，H(0，m)=k2(k2－ 4k+2)/8，

H(0，m) － H(0，1)=(k － 1)4/8，H( ± 1，0)=H( ± c，0) ＜ H( ± 1.2，0)

and H(0，1)=H(0，n) ＜ H(0，m)

Comparing the Hamiltonians of the singular points，we obtain the following results．

Theorem 2

(a)If 1 ＜ k ＜ 1.44，the phase portrait of the system(1)is shown as Fig．1(a)．

(b)If k=1.44，the phase portrait of the system(1)is shown as Fig．1(b)．

(c)If 1.44 ＜ k ＜ 2.3711309，the phase portrait of the system(1)is shown as Fig．1(c)．

(d)If k=2.3711309，the phase portrait of the system(1)is shown as Fig．1(d)．

(e)If2.3711309 ＜ k ＜ 3.4142135，the phase portrait of the system(1)is shown as Fig．1(e)．

(f)If k=3.4142135，the phase portrait of the system(1)is shown as Fig．1(f)．

(g)If k ＞ 3.4142135，the phase portrait of the system(1)is shown as Fig．1(g)．

Proof Because H(x，y)=H(x，0)+H(0，y)，H( ± 1，0)=H( ± c，0)and H(0，1)=H(0，m)we always have H( ±1，1)=H( ± c，1)=H( ±1，n)=H( ± c，n)，H( ±1，m)=H( ± c，m)，and H( ± 1.2，1)=H( ± 1.2，n)，We separately denote H(0，0)，H( ± 1，0)，H( ± 1.2，0)，H(0，1)，H(0，m)，H( ± 1，1)，H( ± 1，m)，H( ± 1.2，1)and H( ± 1.2，m)by h00，h10，hb0，h01，h0m，h11，h1m，hb1，and hbm.

(a)When 1＜k＜1.44，the Hamiltonians of the singular points satisfy the relations

h11＜h1m＜hb1＜hbm＜h10≤h01＜h0m＜h00

or h11＜h1m＜hb1＜hbm＜h10＜h01＜hb0＜h0m＜h00

so the phase portrait is shown as Fig．1(a)．

(b)When k=1.44，we have h10=h01，hb0=h0m，and the Hamiltonians of the singular points satisfy the relations

h11＜h1m=hb1＜hbm＜h10=h01＜hb0=h0m＜h00

so the phase portrait is shown as Fig．1(b)．

(c)When1.44＜k＜2.3711309 the Hamiltonians of the singular points satisfy one of the following relations

h01＜hb1＜h1m＜hbm＜h01＜h0m≤h10＜hb0＜h00，

h11＜hb1＜h1m＜hbm≤h01＜h0m＜h10＜hb0＜h00，

h11＜hb1＜h1m＜h01＜hbm＜h0m＜h10＜hb0＜h00，

so the phase portrait is shown as Fig．1(c)．

(d)When k=2.3711309，we get h1m=h01，and the Hamiltonians of the singular points satisfy the relations

h11＜hb1＜h1m=h01＜hbm＜h0m＜h10＜hb0＜h00，

so the phase portrait is shown as Fig．1(d)．

(e)When 2.3711309＜k＜3.4142135，the Hamiltonians of the singular points satisfy one of the following relations

h11＜hb1＜h01＜h1m＜hbm＜h0m≤h10＜hb0＜h00，

h11＜hb1＜h01＜h1m＜hbm＜h10＜h0n≤hb0＜h00，

h11＜hb1＜h01＜h1m＜hbm≤h10＜hb0＜h0m＜h00，

h11＜hb1＜h01＜h1m＜h10＜hbm＜hb0＜h0m＜h00，

so the phase portrait is shown as Fig．1(e)．

(f)When k=3.4142135，we obtain h0m=0，and the Hamiltonians of the singular points satisfy the relations

h11＜hb1＜h01＜h1m=h10＜hbm=hb0＜h0m=h00，

so the phase portrait is shown as Fig．1(f)．

(g)When k＞3.4142135，we obtain h0m＞0，and the Hamiltonians of the singular points satisfy one of the following relations

h11＜hb1＜h01＜h10＜h1m＜hb0＜hbm＜h00＜h0m，

h11＜hb1＜h01＜h10＜hb0≤h1m＜hbm＜h00＜h0m，

h11＜hb1＜h01＜h10＜hb0＜h1m＜hbm≤h00＜h0m，

h11＜hb1＜h01＜h10＜hb0＜h1m≤h00＜hbm＜h0m，

h11＜hb1＜h01＜h10＜hb0＜h00＜h1m＜hbm＜h0m，

so the phase portrait is shown as Fig．1(g)．

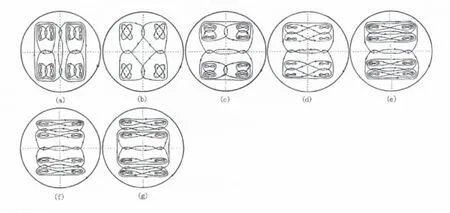
Fig．1(a) ～ (g)The phase portrait of Sy．(1)(a)when(b)when(c)when(d)when(e)when(f)when(g)when

［1］Chen Long－wei，Liu Zhongrong．Classification of phase portraits about planar quintic －equivariant vector fields［C］．Proceedings of the third international conference on nonlinear mechanics．Shanghai University press，1998:769—772．

［2］Li Yan －mei．The global properties of some planar quintic Hamiltonian vector field with equivariant property［J］．Journal of Yunnan University，2001，23(2):87—90．

［3］Li Yan － mei．The classification of phase portraits about some Hamiltonian vector field with equivariant property［J］．Journal of Yunnan Normal University，2003，23(6):5—7．

［4］Chen Guo－wei，Yang Xinan．The Topological classification of plane phase diagram of a class of quintic Hamiltonian system［J］．Mathematica Scientia，2004，24A(6):737—751．

［5］Li Yanmei．Classification of phase portraits of planar quintic Hamiltonian vector field with equivariant property［C］．Proceedings of the international conference on nonlinear mechanics．Shanghai University press，2007:1534—1538．

The Phase Portraits of a type of Planar Septic Hamiltonian Vector Field with Z2－Equivariant Property*

李艷梅
( 楚雄師范學(xué)院，云南楚雄675000)

O175

A

1671－7406(2011)09－0047－04

云南省應(yīng)用基礎(chǔ)研究項(xiàng)目:2008ZC158M。

2011－06－20

李艷梅 (1966—)，女，教授，主要從事非線性微分方程研究。

(責(zé)任編輯 劉洪基)

摘 要:本文給出了一類具有Z2－等變性質(zhì)的七次平面哈密頓向量場(chǎng)的全局相圖，并對(duì)參數(shù)空間進(jìn)行了劃分。

關(guān)鍵詞:七次哈密頓向量場(chǎng);Z2－等變性質(zhì);奇點(diǎn);相圖