柯西不等式證明及應用

黃衛

（南京曉莊學院，江蘇 南京 211171）

柯西不等式證明及應用

黃衛

（南京曉莊學院，江蘇 南京 211171）

本文探討了柯西不等式多種證明方法，通過一系列的例題，反映了柯西不等式在函數求最值及其在幾何上（距離）的廣泛應用.

柯西不等式；證明；應用

柯西不等式是由大數學家柯西（C a u c h y）在研究數學分析中的“流數”問題時得到的.但從歷史的角度講，該不等式應當稱為 C a u c h y-B u n i a k o w s h y-S c h w a r不等式.正因為是后兩位數學家彼此獨立地在積分學中推而廣之，才將這一不等式應用到近乎完善的地步.

在我國的一般高校教育中，微積分、線性代數和概率論是最基本的數學基礎課程.表面上看，這三門課存在很大差異，但與此同時它們卻往往可以從不同的角度和方法對同一事物作出證明及解釋.著名的柯西不等式在不同領域中的證明方式充分說明了人們思維的多樣性、滲透性和完備性.認識這一點可以使思維更活躍，也可以使我們的學習更富有創造性.

1 柯西不等式及其證明

1.1 柯西不等式

柯西不等式擁有多種形式，下面是其幾種形式.

二維形式：(a2+b2)(c2+d2)≥(a c+b d)2等號成立條件：a d=b c

向 量 形 式 ：|α ||β |≥|α·β|，α=（a1，a2,… ,an），β=（b1，b2，… ，bn）（n∈N，n≥2）等號成立條件：β 為零向量，或 α=λβ（λ∈R）.

1.2 下面給出柯西不等式的證明

證明 1（直接法）

則

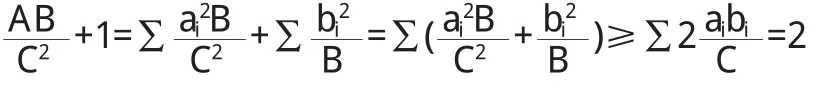
證明 2（利用二次型）

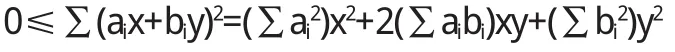
即關于 x、y的二次型非負定，那么

證明 3（數學歸納法）

當 n=k+1時

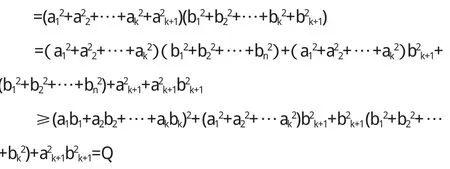
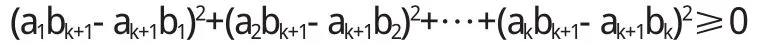
即 n=k-1時，不等式成立
綜上所述，得對對 n∈N+，不等式成立，故得證.
證明 4（利用線性相關證明）
經過仔細探討發現，為了嚴格而簡潔地刻劃出（a1,a2,…, an）與（b1,b2,…,bn）具有什么 關系 時才成為柯 西不 等式 中等號成立的充要條件，我們從向量線性相關、線性無關的概念出發，來敘述并證明這種特殊的柯西不等式.設 Rn為向量空間.

當且僅當向量ζ與η線性相關時，

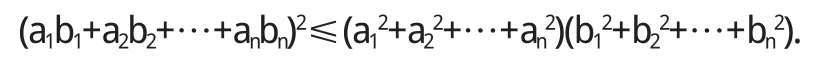
證明

（ⅰ）設 ζ、η 線性相關，則存在不全為 0的 k、1∈Rn,使k ζ+l η=0

無論何種情形代入柯西不等式兩端便知等號成立.

（ⅱ）設 ζ、η 線性無關，則對每個 x∈R.有 ζ-x η≠0,即至少有一個 i,1:i:n使 ai-bix≠0于是

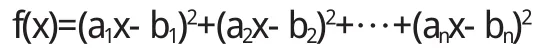
或

這里 η≠0，否則 ζ、η 線性相關與題設矛盾.

于是有 b1,b2,…,bn不全為 0和這樣推出△＜0

即

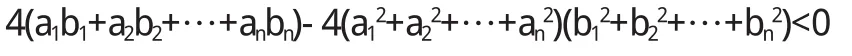
于是

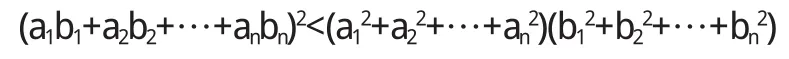
（ⅲ）若柯西不等式等號成立.則 ζ、η 必線性相關.不然由（ⅱ）將推出柯西不等式等號不成立.證畢.

以上嚴格的命題敘述和證明，是把高等代數對一般抽象歐氏空間相應命題及其證明改寫為特殊形式.

3 柯西不等式的應用

例1（距離問題）

利 用 柯 西 不 等 式 證 明 ： 平 面 點 p(x0,y0)到 直 線A x-B y-C=0的距離公式

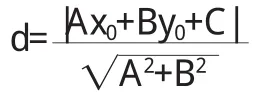
證明 對直線上的任意一點 Q(x,y)，得 A x-B y=-C，且A2-B2>0

由柯西不等式，得

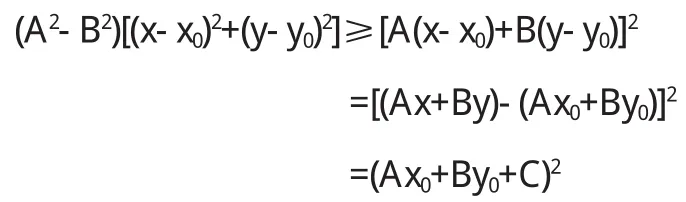
則，有

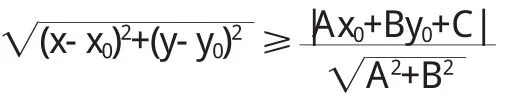
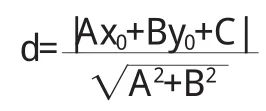
以上證明運用的背景均在二維平面內，由此可以考慮發展到三維空間點到面的距離公式，在 n維抽象空間中，球點到空間中任意點的距離最小，這就是極值的問題.

例2（極值問題）

如果 x1+…+xn=1,a>0，那么當且僅當 a1x1=…=anxn時，f(x)的最小值是

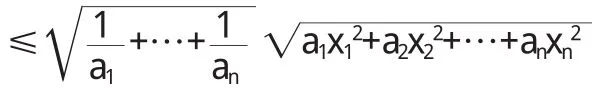
以上證明的是一個極值問題，是在 x1-x2-…-xn=1的條件下成立.如果把此條件推廣成，求 f(x) =x1+x2+…+xn的最大值，一樣能夠求得.

上面我們介紹了柯西不等式及各種形式，并證明了一般形式，在此基礎上并闡述了它的一些應用.

〔1〕徐 幼 明.柯西不 等 式的推廣 及 其應用[J].數 學 通 訊 ，1996（12）:25-26.

〔2〕王蓮花，李曄，李戰國，劉芳.柯西不等式的證明及應用研究[J].河南教育學報，2003，12（1）：5-7.

〔3〕王玉蘭.柯西不等式的一個簡單證明及其應用[J].內蒙古科技與經濟，2002（8）：135.

〔4〕劉 治 和 .淺 談 柯 西 不 等 式 的 證 明 及 應 用 [J].數 學 通 報 ，2000，18（5）：44-46.

〔5〕 方海燕. 柯西不等式的應用 [J]. 數理天地 （高中版），2005，13（10）：21-23.

O 1 7

A

1673-260X（2011）04-0015-02