基于復雜網絡特征的P2P系統模型的研究
王曉燕,毛紅閣
(南陽師范學院軟件學院,河南南陽473061)
基于復雜網絡特征的P2P系統模型的研究
王曉燕,毛紅閣
(南陽師范學院軟件學院,河南南陽473061)
研究表明小世界和無尺度是很多大型復雜網絡的重要特征,研究具有復雜網絡特征的P2P網絡模型對研究網絡的拓撲結構和行為有著重要的意義.針對現有模型不能全面地反映實際網絡提出了基于復雜網絡特征的P2P網絡模型.本文在基于組增長和選擇具有較大吸引力的節點這些特征基礎上建立一個新的模型,經過實驗證明此模型更接近實際網絡.
復雜網絡;P2P;靜態參數
小世界和無標度出現以后,引發了許多學者對復雜網絡模型的研究.吳艾等學者提出了基于組增長的Sale-free網絡模型[1],劉美玲等學者提出了擇優選擇節點構成的復雜網絡模型研究[2],這些研究沒有考慮真實網絡的大部分特征,而是一部分特征的刻畫.在上述兩文中節點加入網絡都是以概率進行擇優連接的,而在真實系統中一個節點的連接不僅與節點的度數有關而且與節點的吸引度有關[3].例如,在網絡中,有些網站創建更好的內容吸引瀏覽者,可以在更短的時間內獲得大量的連接反而超過那些創建時間很早的網站.這說明一個簡單的模型相對于系統中其它的節點,有些節點能以更高的速率獲得連接數量,我們把這些不同歸結于節點本身具有的吸引力的大小,我們把節點具有的吸引力稱之為吸引因子.為了更好的刻畫實際網絡,提高網絡的魯棒性,降低其脆弱性,本文對建立p2p網絡模型提出了一下幾點:
(1)復雜網絡的形成是一個動態的成長變化的過程;
(2)網絡的增長不需要全局擇優,而是部分擇優;
(3)網絡中多個節點以組的方式加入也是網絡的增長方式;
(4)新增節點與吸引因子較大的節點相連接;
綜上所述,本文提出了P2PSM(P2PSystemModel)網絡模型.
1 P2PSM的建立過程如下
初始網絡中有n個節點,e條邊,節點的吸引因子即為β,ki為結點i的度數,βi為節點i的吸引因子,模型的建立過程如下:
(1)開始時,網絡中有n個節點,e條邊,該網絡即為G(n,e).
(3)組的增長:
①生成組:
每次添加一組n個節點組成網絡G',模型中G'由兩步得到:
a:首先,生成不同ki的規則的連接圖,ki的值等于每個節點與鄰居相連的邊數k0(模型中k0≥3),根據需要決定ki的多少.
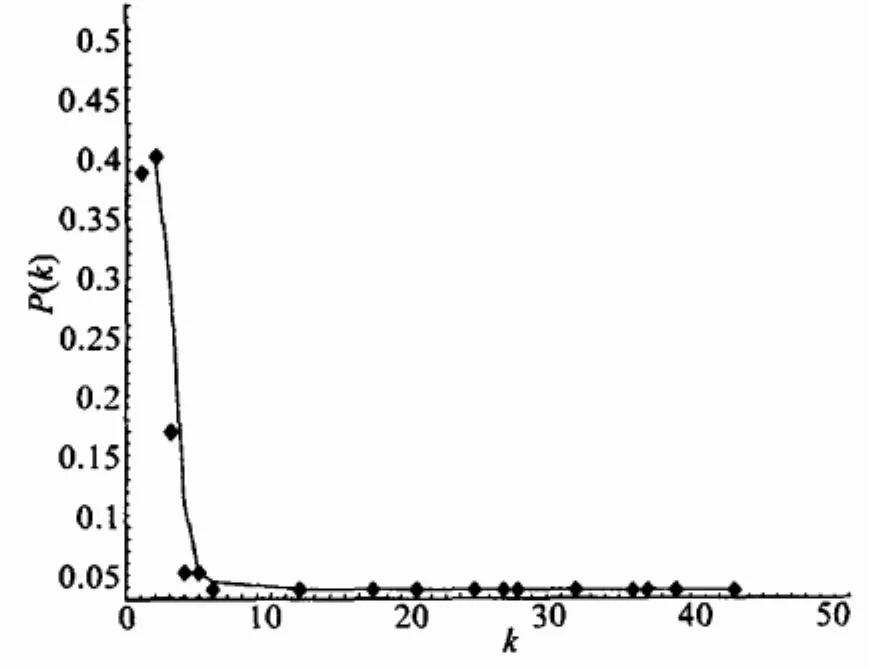
b:然后,重連上述規則網絡圖的一些邊,在G'中隨機選擇兩個節點且vj'≠vi',按概率p在vi'和vj'之間建立連接 ②加入組: 每隔一定時間t,加入一組帶有et條邊的節點,以概率連接到局域世界G(ni),若邊數ei>r,則多余的邊加到G(ni)之外的節點上. (4)在每加入1組節點后,計算G(ni)中每個節點的度數,如果某些新加入的節點(假設有s個)ei>min{ki}(ki為老節點連接新節點后的度數),則把這s個新節點也看作老節點,則以后再加入的節點組,再以概率(i,j=1,2,…N)連接到s+r個結點上. 本算法第一步從一個小型網絡開始,從現實網絡來看,很多節點局部擇優加入網絡,網絡中節點被連接的概率與節點的吸引力大小有關,并且節點的加入可能是以組的方式加入,本模型從整體上考慮了現實網絡的特性,我們通過調節βi和p控制整個網絡. 下面舉例說明,真實網絡的增長過程: (1)初始一個小網絡G(30,90),即帶有30個節點,90條邊; (3)每隔一定的t時間,加入一組(10個節點,k0=4,p=0.15)帶有ei條邊的節點以概率與G(ni)連接. (4)每加入20個節點計算G(ni)中每個節點的度數. 經過了10t的時間且加入了236條邊;經過計算得共有6個新加入的節點度數ei>{kni}.網絡G(30,90)變成了新網絡G(30+100,90+236)=G(130,326),G(ni)變為G(ni)(i=1,2…11). (1)通過continuum理論[4,5]來分析模型的度分布,對度分布進行數值擬合運算可得服從冪率分布P(k)=ak-r,r=1±0.3,見圖1所示. 圖1 度分布示意圖 證明因為通常p的取值都較小,所以認為G'加入之前每個節點的度為k.忽略重連對G'中節點度的影響.每個組的加入近似看成是n個節點逐個加入的,每個單位時間t加入一個節點,并滿足: 解微分方程得: 該方程的相對初始條件是每個節點i在ti時刻到達系統連通度ki(ti)=ei,所以上述解應為: 則節點連通度ki(ti) 因為節點是等時間間隔添加到系統的,所以ti的概率分布是一個均勻離散分布列為: 帶入方程可得: 當t趨于+∞時可得r=1,由于取得節點較少,所以誤差很為±0.3. (2)利用UCINET軟件計算并分析P2PSM與B-A模型的靜態統計量,如下表所示: 表1 靜態特征參數表 從表1可以看出: ①擴展模型生成的網絡其度分布也服從冪律分布,但冪指數很小,說明這個網絡冪律特征沒有B-A模型生成的網絡明顯,所以它魯棒性更好; ②從聚集系數和最短路徑上可以看出改進的模型生成的網絡集聚性更強一些,由于B-A模型的全局擇優機制,所以平均路徑要比擴展模型的網絡更短一些,但改進模型的擇優更減少了節點的工作量,而改進的模型搜索速度快,這也更加符合現實網絡; ③改進后的模型考慮了節點以組的方式加入,所以該模型有助于建立更接近實際的網絡拓撲結構和網絡的動態成長過程,從而能更準確地分析、設計和評測與網絡結構和行為相關的工作. 〔1〕吳艾,劉心松,劉丹,左朝樹.基于組增長的小世界Scalefree網絡模型[J].計算機科學,2005,32(7). 〔2〕劉美玲,王仲君.擇優選擇節點構成的復雜網絡模型研究[J].系統工程與電子技術,2006,28(4). 〔3〕陶少華,楊春,李慧娜,張勇.基于節點吸引力的復雜網絡演化模型研究[J].計算機工程,2009,35(1). 〔4〕郭雷,許曉鳴.復雜網絡[Z].上海:上海科技教育出版社,2006. 〔5〕Reka Albert*and Albert-Laszlo Barabasi.Statistical mechanics of complex networks[J].REVIEWS OF MODERN PHYSICS,VOLUME 74,JANUARY 2002. 通過實驗證明,P2PSM模型更有利于我們對現實網絡的認識.P2PSM模型也有一些缺點:它只考慮了節點的加入,沒有考慮到成組的結點的刪除;在實際網絡中大部分節點是異質的,我們建立模型時,把所有節點當作同質的進行構造,會產生一些誤差. TP393 A 1673-260X(2011)01-0023-022 舉例分析
3 參數分析
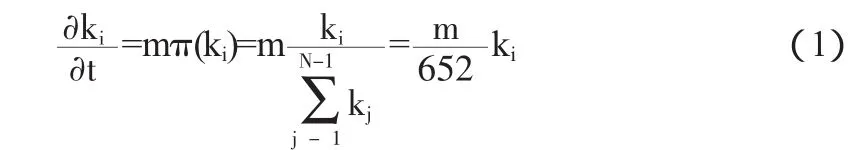




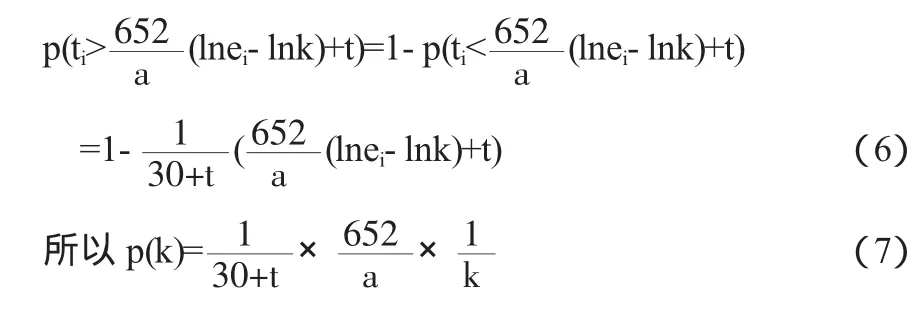

4 結論

