變靜為動促進學生動態思考——記多媒體教學“形變積不變”

☆ 王小林

（重慶市萬州區雞公嶺小學，重慶 404100）

我等幾位教師曾面對一道平面幾何證明題，百思不得其解，于是擱置一邊。偶然讀到了一本《數學分析》，看到了一種“動態思考”的方法，受到極大啟示——再拿原題來想，能否把其中的某部分轉動一下呢？于是試著把其中一個三角形旋轉，與另一個三角形組成新圖，結果發現了全等關系，很快完成了證明，心中好生喜悅！不但破了一道難題，而且學到了一種非常規的思考方法，感悟到靜態思考的局限性和動態思考在解決問題中的奇妙作用，于是激發起自己培養學生“動態思考”求解問題意識的教學激情。

過去受到教學設備的限制，對學生這方面的培養和訓練難以展開。有了多媒體技術后，方顯如魚得水，更產生了興趣。于是積極開展“多媒體技術在數學教學中的有效應用”的實驗。力求根據教學內容合理使用多媒體技術，充分利用多媒體的動畫功能，使靜態的數學問題的解決思路實現動態呈現，不僅為強化“雙基”，更想“沖擊”小學生靜止地看待、思考、解決問題的思維定勢，建構“動態思考”模式。現結合人教版第九冊“多邊形的面積”的教學介紹如下。

一、教學過程回顧

1.等底等高等面積——新課孕伏

一層，初學“平行四邊形面積”時，在引導學生通過數方格、割拼等方法探索面積計算方法的過程中，感受平行四邊形的底、高與長方形的長、寬分別相等，則面積相等。

二層，在學生測量和計算的過程中體會等底等高的平行四邊形面積相等，為滲透“動”的觀點，教師用動畫（如圖1） 演示高h和平行四邊形EFGH都沿著兩條平行線滑動，在動態中強化這一關系。

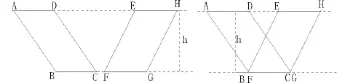
圖1

三層，結合“三角形面積”的學習，進一步突出“等底等高的三角形面積相等”。先讓學生通過計算自己感受“規律”（如圖2）。這兩個三角形的面積怎樣？你想到什么？”。再從動的角度領會規律（如圖3），動畫演示高h沿著兩條平行線滑動,說明規律；再使△DBC的D點沿著所在直線滑動，在“咝咝”的伴音中△DBC逐漸變形并與其余三角形完全重合，此時學生確信只要底、高不變面積始終不變，并直觀感受到了“動態變形”的過程形象。經過鞏固練習，到“梯形面積”學習之前，平行四邊形和三角形中的“等底等高，等面積”的規律形成了概念，為下一步教學筑好了“出發陣地”。

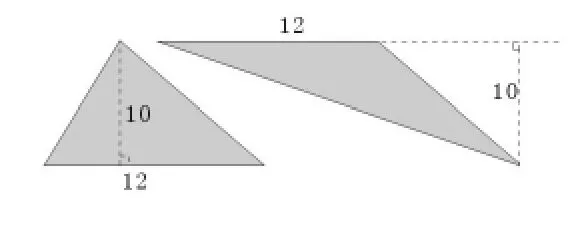
圖2

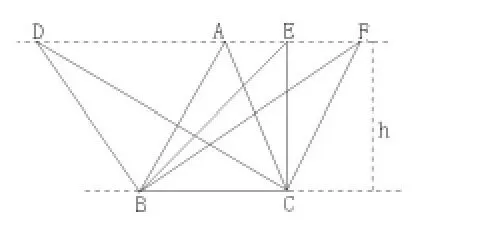
圖3

2.形狀變化積不變——構建認知

一層，求平行四邊形BCEF的面積（如圖4）。學生利用等底等高的關系試算后，教師用動畫使平行四邊形BCEF平移變形、重合。突出了“形變積不變”的成象及成因。

圖4

二層，求兩個陰影三角形的面積和（如圖5）。學生經過觀察、作圖、思考。有的想到了用分割的方法解答，教師用動畫演示驗證了分割法——空白部分與陰影部分的面積相同，則陰影面積是長方形面積的一半；追問：有別的想法嗎？學生觀察思考了好一會，終于有學生說：能不能向前面⑷題那樣移動，把陰影三角形拼在一起呢？想得好！教師及時用動畫（如圖6）演示，學生們清楚地看到，一個三角形的一個頂點順所在邊移動，兩個三角形“揉捏”成了一個大三角形，但是每個三角形的底和高始終未變，所以“揉捏”成的大三角形的面積就是原來的陰影面積，于是巧解:12×8÷2。

圖5

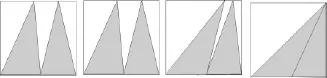
圖6

三層，結合“梯形面積”的學習深入訓練。如圖7，求陰影部分的面積。學生試解此題，多數學生用梯形面積減去三角形面積的方法（靜態思維在頭腦中根深蒂固,動態思考的構建尚需時日），只有極少數學生直接用“20×25÷2”，教師大加贊賞。在學生介紹思路后，用動畫演示（如圖8）。學生看著動畫的演示，口中“嘖、嘖”有聲，“動態思考”在學生頭腦中開始扎根。

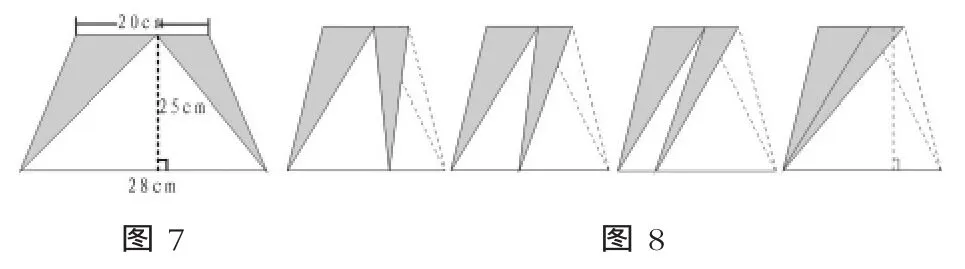
3.動態思考解問題——嘗試應用

結合“多邊形面積”的學習，在綜合練習中進一步要求：觀察思考，用不同的方法解題，方法巧妙者把圖形畫出來，如果做對，打A＋。學生在下面各題的解答中表現出靈活性，“動態思考”在學生的頭腦中逐漸成長。

如圖9題梯形中的A、B兩部分的面積大小怎樣？如圖10、圖11求圖中的陰影面積。

這些題都可用不同思路解答，在肯定正確的基礎上讓學生著重說明“變形”的方法。圖9列式為（80－2－3）×30；圖 11列式為 6－1.5）×2÷2，是這一方法的直接表達式。

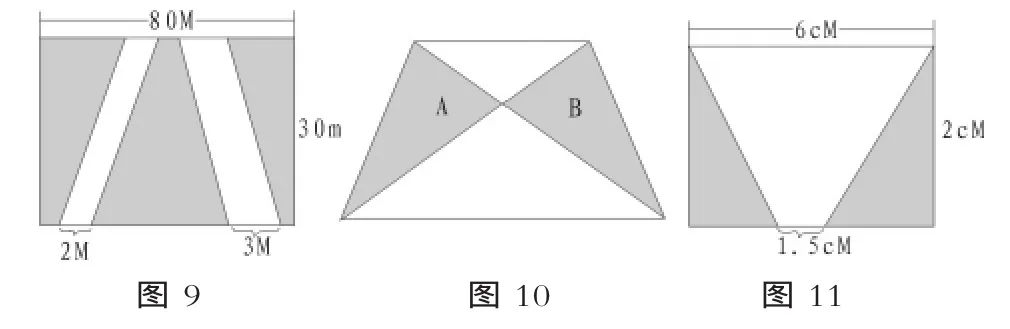
其中圖9只需陰影部分順平行線平移即可，圖10需其中一個最大三角形的一個頂點沿梯形的上底移動揉捏變形，與另一個大三角形重合，反映出A、B面積相等；圖11中的一個三角形既要整體平移，也要“揉捏變形”與另一個三角形合成一個大三角形，可見對這一類問題思維要求較高，由于多媒體的介入，教與學都覺較易。

再看思考題（如圖12），直角梯形的面積是96平方厘米，E、F兩點分別是兩腰的中點，請算一算陰影部分的面積和。學生獨立思考，困難極大，部分學生用割拼的方法解答，少數學生能用“旋轉”的方法，于是教師用動畫（如圖13）驗證，變形過程一目了然。

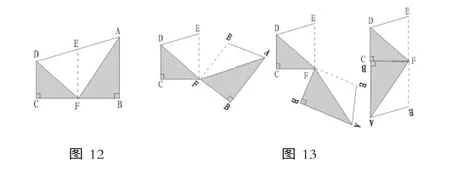
4.辛勤耕耘終結果——初見成效

“多邊形的面積”學習結束，在單元質量檢測時，我加了一道選作題（如圖14）：已知兩條平行線間的距離是3m，求平行四邊形與三角形的面積和。結果兩個班各有二十幾位學生（如圖 15）解答，巧列式為（1.2＋0.8＋1.2）×3÷2

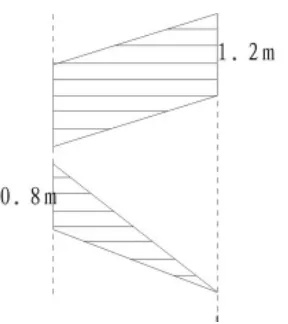
圖14

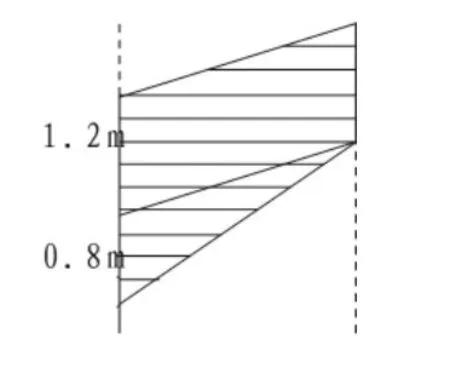
圖15

無獨有偶，在期末的質量檢測中，出現一題（如圖16），梯形中有一個最大的正方形，求圖中陰影部分的面積。我班約56名學生動態思考，列式為：（6＋8）×12÷2。其余班級學生大多是常規思考，列式為：（12＋6＋8＋12）×12÷2－12×12。兩種方法反映出計算的“簡”與“繁”和思維的“動”與“靜”的差別。

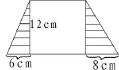
圖16

二、反思其喜與憂

1.利于建構動態思維模式

世界是永恒運動著的物質世界。要反映物質運動的速度、方向、位置、相互關系，需要數學去研究。數學思維有其內在的邏輯的嚴謹性，必須引導學生學習、掌握、運用邏輯推理的方法，去進行環環相扣的思考。同時在研究、解決物體的運動問題——天體之謎、火箭之速、衛星之軌及物體內部的形變問題等，離不開動態地思考。需要從小對學生進行動態思考的教育。那么如何開展這方面的教育呢？筆者以為，可以充分利用多媒體技術直觀演示——把靜態材料加工、變式、變形、動態重組為簡化的與原問題等值的新問題的過程，促使學生感知動態思考的形象、建立表象、不斷調整認知結構、插補動態思考模式、逐漸豐富問題解決的策略系統。

“動態思考”屬于形象思維，學生有了這種思維認知后，看到相關問題，自然會在腦中產生表象，“動態思考”加工圖形，得以問題解決。如果從平面問題到立體問題堅持這樣教學、訓練，對培養、提高學生的空間想象力來講，定會大有益處。

2.利于建構轉化思想方法

轉化思想是重要的數學思想之一。這種思想的建立，必須在長期的教學中、在各種教學材料中逐漸滲透，潤物細無聲。“形變積不變”的教學內容是極好的載體，便于教師充分發掘其中“動”的思維因素；多媒體技術是強有力的手段，動畫的變形演示形象直觀地凸顯了“轉化”的過程，不僅是化難為易解決數學問題，更重要的是通過“變形”、“重組”、“解決”的過程促使學生構建“轉化”的思想。

3.是否與教改精神相悖呢

新“課標”要求教師積極引導學生自主學習、探究、發現、建構新知。這在大量的基礎知識、基本規律的探索教學中是完全可行的。但對于有些知識難點、知識條理性的整理以及學生可借鑒的生活原型及知識儲備缺乏的內容還得依靠教師及時介入。象這種“動態變形”來講，學生確實難以搜索到可借鑒的生活原型及方法經驗，不可能突發奇想，自主發現這種思維方式。

盡管學生已有了“平移”和“割拼”的經驗（還未學“旋轉”），但稍加分析即可發現，這些經驗有很大的局限性——平移時，純粹是整個圖形位置移動；割拼時，往往是某個圖形的部分被分割，這個部分也是整體移動，這些變化都不會把原圖進行“揉捏”變形。對于揉捏式變形學生暫時沒有直接借鑒的基點，必須教師發揮主導作用，以有效的手段，逐漸滲透這種動態思考模式。如前所述，從平行四邊形的高沿順底邊滑動、整個圖形在高不變的條件下揉捏變形開始，到用這種方法求陰影面積；學生通過首次感受、初步應用、問題解決，思維在波浪式推進。

首次出現這種變形過程，肯定要教師一邊演示，一邊啟發學生觀察、感受過程，那么，這時讓學生聽講與看多媒體演示是否與教改精神相悖呢？筆者不免有些誠惶誠恐。

我想，目前依然存在著“接受式”與“發現式”等學習理論。在教學實踐中，它們都應有“用武之地”。“教改”要求把學生置于學習的前臺，旨在培養探究意識，也是對傳統的“填鴨式”、“滿堂灌”的矯正，但不會完全否認“接受式”學習方式，特別是那些無法通過探究發現的知識與方法，教師不教咋辦？對于學生相對靜止的思維定勢不破則不立，多媒體豈不是“破”與“立”的快捷適用的工具？這樣一想，便心中稍安！