從Fermat大定理看數學問題在數學發展中的作用

劉幸東

（肇慶學院 數學與信息科學學院，廣東 肇慶 526061）

從Fermat大定理看數學問題在數學發展中的作用

劉幸東

（肇慶學院 數學與信息科學學院，廣東 肇慶 526061）

回顧費馬大定理的解決過程,從一個側面論述了數學問題對數學發展的推動作用．

Fermat大定理；數學問題；數學發展

1994年10月25日，美國俄亥俄州州立大學的盧賓（Karl．Rubin）教授用電子郵件向世界宣布：安德魯．維爾斯（Andrew Wiles）完成了對費馬大定理的證明．1995年5月，《數學年刊》用整整1期發表了維爾斯的論文．至此，費馬大定理最終成為一個真正的定理，一個困擾人間智者300多年的著名問題被完全解決了．這項成果被認為是20世紀最偉大的科學成就之一．1996年3月，維爾斯榮獲了沃爾夫獎，1998年獲得特別菲爾茲獎[1]46．

費馬大定理是一個有關不定方程的問題．1621年，古希臘數學家丟番圖所著《算術》一書被從希臘文譯成拉丁文在法國出版．1637年，法國數學家費馬對該書中的數論問題進行了研究和推廣，對于該書第Ⅱ卷中的第8命題“將1個平方數分為2個平方數”，他想到了更一般的問題．他在該書頁邊處用拉丁文寫了一句話，大意如下：

“將1個立方數分為2個立方數的和，1個4次冪分為2個4次冪的和，或者一般地將1個高于2次的冪分為2個同次冪的和，這是不可能的．關于此，我確信已發現一種奇妙的證法，可惜這里的空白太小，寫不下了．”

若用現代數學語言進行描述，可以將其敘述如下：

當整數n＞2時，方程

xn＋yn＝zn

沒有正整數解．

這就是著名的費馬大定理．該問題從提出到1994年被維爾斯解決，整整歷時358年．一代又一代數學家和數學愛好者為此付出過艱辛的努力，文獻[2]敘述了歷代數學家前赴后繼尋求費馬大定理的證明歷程．伴隨著征服費馬大定理的艱辛過程，同時產生了數學的新思想、新分支，這些分支在很大程度上影響了現代數學的發展方向．費馬大定理的解決之路，充分顯示了數學問題在數學發展中的作用．下面通過對解決費馬大定理中一些重大階段的回顧，從一個側面論述數學問題對數學發展的推動作用．

1 無窮遞降法

盡管費馬在那本《算術》書中從未寫過費馬大定理的證明，但在書中別的地方隱蔽地描述了對特殊情況n＝4的證明，并且在一個完全不同的問題的證明中采用了這個證明．這是一種特殊形式的反證法，稱之為無窮遞降法．

為了證明方程x4＋y4＝z4沒有正整數解，費馬從假設存在一個正整數解

x＝X1,y＝Y1,z＝Z1

著手．通過研究X1,Y1,Z1的性質，費馬能夠證明：如果這個假定解確實存在，那么一定會存在一個更小的解X2,Y2,Z2(Z2＜Z1);然后再通過研究這個新解的性質，又能證明存在一個還要小的解X3,Y3,Z3(Z3＜Z2),這樣一直進行下去．于是費馬找到了一列逐步遞減的解，理論上它們將永遠繼續下去，產生越來越小的解，然而，x,y和z必須是正整數，因此這個永無止境的正整數解是不可能存在的，因為必定會有一個最小的可能解存在．這個矛盾證明了最初的關于存在一個解X1,Y1,Z1的假設一定是錯誤的．使用無窮遞降法，費馬證明了n＝4時這個方程無xyz≠0的整數解．

費馬的無窮遞降法的證明思想實際上是反證法的證明方法和最小數原理的完美結合,因此現代數論利用費馬遞降法證明一個丟番圖方程沒有正整數解時，通常假設該方程存在正整數解，則由最小數原理可以假設Z0是某個變元Z的所有正整數解的集合中的最小值；再利用解的性質及數學推理方法證明可以找到該丟番圖方程的另一組正整數解，其中Z的值Z1＜Z0，與Z0的最小值的假設矛盾，從而證明了該丟番圖方程無正整數解．

隨后的100多年間，數學家們嘗試用費馬的無窮遞降法研究除n＝4之外的情形，但均以失敗告終．

1753年，萊昂哈德·歐拉(Leonhard Euler)引入虛數，成功運用無窮遞降法證明了n＝3的情況，這是費馬去世1個世紀后對費馬大定理研究的突破性進展．

由于證明了n＝4無正整數解，所以也就證明了n被4整除，即n＝4k（k為正整數）時，方程xn＋yn＝zn無正整數解．因為若x4k＋y4k＝z4k有正整數解x1,y1,z1，則x4＋y4＝z4將有正整數解x1k,y1k,z1k,這與前面的結論矛盾．利用同樣的原理，歐拉對n＝3的證明，自動地證明了n＝3k(k為正整數)的情形．特別有意義的是3為素數，這使得數學家們看到，只要其他素數情形費馬定理成立，那么對n的一切值就證明了費馬大定理成立．可惜素數的無窮性使早期證明費馬大定理的希望破滅．

2 熱爾曼素數

自1753年歐拉對費馬大定理的研究取得突破性進展后，數學家們徒勞地試圖一一證明其他情況．事隔75年，法國女數學家索菲·熱爾曼(Marie-Sophie Germain)采用了一種新的策略：并不去證明一種特殊的情形，而是一次就得出適合許多情形的解答，她的方法是針對使（2p＋1）也是素數的素數P（稱為熱爾曼素數）進行．熱爾曼的素數P包括了5，因為11×(2×5＋1)也是素數；但不包括13，因為27×(2×13＋1)不是素數．她巧妙而大致地證明了熱爾曼素數方程xn＋yn＝zn不存在正整數解．

1825年，狄利克雷(Dirichlet)和勒讓德(Legendre)的工作使熱爾曼的方法獲得完滿成功，他們獨立地證明了n＝5不存在解．14年后，加里布爾·拉梅對熱爾曼的方法做了進一步巧妙的補充，證明了n＝7的情形．

3 理想數的建立，分圓域理論的研究及代數數論的創立

此后直到1857年，法國數學家拉梅(Lamé)和柯西(Cauchy)都試圖利用分圓整數理論證明費馬大定理，但可惜的是分圓整數唯一因子分解定理不成立．德國數學家恩斯特·庫默爾（Ernst Kummer）為使唯一因子分解定理成立，從1844年開始了一系列研究．對每個奇素數p，他將費馬方程分解成

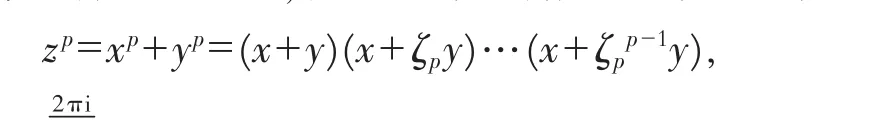
正是由于庫默爾等人的研究，1871年以后戴德金(Dedekind)推廣了高斯的復整數和庫默爾的代數數理論，由此創立了現代代數數理論．過去代數數論本來是研究費馬大定理解的一種方案；而現在，其自身卻變成了一門新興學科．其創立被認為是19世紀代數學學科的最大成就．

隨著對費馬大定理研究的深入，數學家們清楚地認識到：只要證明了谷山一志村猜想（即每個橢圓方程必定是模形式），那么就隱含費馬方程無解，于是就可立即證得費馬大定理．

英國數學家安德魯·維爾斯奮斗了7年，終于以《模形式、橢圓曲線和伽羅畢表示》、《模曲線和費馬大定理》和《海克代數的環論性質》等一系列成果，證明了谷山一志村猜想及費馬大定理．至此，一個困擾了人間智者358年的謎終于被解開．

在費馬大定理的攻克歷程中產生了許多新思想、新方法與新分支．這充分證明了數學問題對數學發展具有積極的推動作用．正如希爾伯特（Hilbert）[1]401900年在世界數學家大會上所言：“對費馬大定理的研究提供了一個明顯的例子，說明這樣一個非常特殊、似乎不十分重要的問題會對科學產生怎樣令人鼓舞的影響．受費馬問題的啟發，庫默爾引進了理想數，并發現了把分圓域的理想數分解為理想質數的唯一分解定理，這個定理今天已被戴德金(Dedekind)和克羅內克（Kronecker）推廣到任一代數數域，在近代數論中占有中心地位，其意義已遠遠超出數論的范圍而深入到代數和函數論的領域．”

數學上還有許多數學問題與數學猜想，隨著這些問題、猜想的解決，勢必會推動數學更進一步向前發展．

[1] 閔嗣鶴,嚴士健.初等數論[M].3版.北京:高等教育出版社,2005.

[2]西蒙·辛格.費馬大定理——一個困惑了世間智者358年的謎[M].上海:上海譯文出版社,2005.

The Role of Mathematic Problems in the Development of Mathematics from the Solution of the Fermat’s Last Theorem

LIU Xingdong

(School of Mathematics and Information Sciences,Zhaoqing University,Zhaoqing,Guangdong 526061,China)

From reviewing the solution of Fermat's last theorem,how the mathematical problems promote the improvement of mathematical from the other side is mainly discussed.

Fermat’s last theorem;math problems;math development

G655

A

1009－8445（2011）02－0015－03

（責任編輯：陳 靜）

2011－02－14

廣東省高等教育教學改革工程項目（BKYBJG20060278）

劉幸東(1960－),女,河北邢臺人,肇慶學院數學與信息科學學院副教授．