大鍛件統計學Chi-square test的研究和應用

齊作玉 呂亞臣 任運來

(上海重型機器廠有限公司，上海200245)

1 問題的提出

我國大鍛件的生產能力正隨著液壓機設備能力的提高而相應提高，在國際上也逐步處于領先水平。我們在大鍛件的攻關創新方面也取得了很大突破。但是，我國大鍛件的總體質量控制水平離世界先進水平還有不小的差距。各大重機廠工藝開發人員會碰到這樣的情況，開發的新產品生產成功了，但之后用同樣的工藝卻意外出現了不合格品。在許多情況下，人們不能確切知道大鍛件的質量好是怎么好的，壞是怎么壞的。

大鍛件通常是重大設備的關鍵部件，生產難度高、周期長、價格貴，一旦一件報廢就會給生產企業和使用企業造成巨大的經濟損失。因此，如何穩定控制大鍛件的質量就成為了我國大鍛件生產企業迫切需要解決的問題。

專家個人經驗的價值不可否認，對分析判斷質量問題有相當大的作用。尤其是在模糊不清、無所適從的時候，專家意見為問題的處理加快了節奏。然而，對于重復性出現的質量問題，我們就不應當總是依賴于專家個人的主觀意見，而是應當升級為客觀科學的系統意見和可靠的方法。

從質量管理的角度，加強過程記錄、強調細化和優化工藝都是從根本上解決質量不穩定問題的一些基本方法，這些基本方法是穩定控制大鍛件產品質量的必由之路。但是，加強過程記錄本身不能直接對鍛件產品質量產生控制作用，只有在科學分析和合理利用過程記錄的數據之后，才能知道原來過程的好壞，才能知道如何進一步控制產品的質量，才能知道如何實現細化優化工藝和達到從工藝上控制產品質量的目的。

對于過程記錄和生產數據，站在科學的角度，我們不能就數論數下結論。而應該對數值加以必要的統計學處理再下結論。

統計學是以概率論為根據，對收集的數據，透過帶有偶然性的數據來認識事物的本質，說明各個事物間的關系，論證事物的發展規律。統計學在應用上是很廣泛的，目前它已幾乎應用于所有科學技術領域以及工農業生產和國民經濟的各個部門之中，許多行業都充分顯示出了統計學在科技進步上的重要性和有效性。

遺憾的是，統計學在大鍛件生產科研領域里的應用目前還非常薄弱，甚至很少見到大鍛件統計學應用實例的報告、論文和書籍。即使國外發達國家的一些先進企業實際上正在享受該技術帶來的成果，但也沒有關于這方面技術訣竅的介紹。比如，美國TIMKEN是一家擁有94年煉鋼歷史的特種鋼生產廠，其常用牌號450種，包括航空航天用鋼。該企業是近百年美國最好的、最值得信賴的合金鋼制造廠家。其化學檢測表明，TIMKEN鋼包精煉鋼的潔凈度已達到或超過我國電渣鋼水平。進一步分析該企業，可以發現，它的成功離不開它的統計學應用基礎。尤其是它的潔凈鋼技術[1]，以實測化學成分與目標數值的差異為不斷跟蹤統計和分析的內容，并成為其多年積累的精益求精的質量控制要求。

傳統上之所以統計學在大鍛件生產領域里的應用較少，主要有三個困難：(1)大鍛件的生產特點是產品品種多，單件、小批量生產，產品生產周期長，工藝影響因素多，這為有效開展統計分析帶來一定的困難；(2)大鍛件熱加工生產工序主要是特殊工序[2]，國內大鍛件生產大都還沒有建立定量的過程(工序)能力的控制，一些工藝細節還沒有定量化或參數化[3]的設計，生產過程細節也沒有定量或參數化的記錄，無法開展統計分析；(3)概率論統計學本身不太容易被理解和掌握，在大鍛件領域里，成功應用的方法和實例也非常少，缺少實例和方法能直接借鑒和引用。這說明，統計學在大鍛件領域的統計學應用基礎還比較薄弱。

本文根據大鍛件生產的特點和統計學的基本理論方法，首次深入淺出地論述了大鍛件的Chi-square test，即X2檢驗，并給出了具體應用示例。該方法可用于大鍛件工藝參數的科學分析和生產驗證，可用于大鍛件質量分析和判斷，可幫助逐步建立起大鍛件的工序能力，幫助實現穩定并提升大鍛件工藝和質量控制水平。

2 X2檢驗

統計學研究的結果表明，我們應該根據所抽取樣本量的大小來選擇不同的顯著性檢驗方法。通過對統計學方法的分析歸納，可以得出如下觀點：

對于計數資料的顯著性檢驗，當樣本含量較小，200例以下，選用X2檢驗；當樣本含量較大，200例以上，則選用u檢驗。

對于大鍛件的生產和計數資料的分析，根據以上觀點，我們顯然應當選擇X2檢驗。當然，在大鍛件統計學應用發展到一定時期，有了足夠的歷史積累之后，大樣本統計應用和其它方法也可能會得到充分應用。

X2檢驗是一種用途較廣的假設檢驗方法。主要用于計數資料的分析，如兩組(或幾組)樣本率(或構成比)之間有無差別和計數資料的相關分析。對于大鍛件熱加工工藝的研究，我們完全可以用它來科學分析某一工藝參數對產品質量結果的影響程度。

關于計數資料樣本的大小，研究者們提出了，在頻數或相對數的應用時，分母要求在30例以上。30例以下為分母計算的相對數應用時，需要加以說明。至于以10例或8例為分母來計算的相對數，會給人造成誤解。除非精密設計實驗、精選實驗對象、嚴格控制實驗條件。這就是說，對于X2檢驗，每組適合的樣本量應該在11到200之間。為此，本文把X2檢驗最小樣本量定義為11。

我們根據文獻[4]的中心壓實的鍛造條件，可以推導出鍛造工藝方法的拔長比條件。該條件可以為單件和小批量生產的大鍛件的統計創建一個同質的條件(具有相同性質的觀察單位稱為同質，否則稱為異質)，從而擴大了我們抽取樣本量的統計范圍。

文獻[4]報告，曾隨機抽查了144只有超聲波探傷報告的大鍛件，并根據宏觀控制鍛造法的拔長比條件對所有鍛壓工藝進行了分析驗算，得出了統計數據。為了幫助大鍛件年輕一代工藝人員完全掌握統計學應用方法，這里介紹X2檢驗的具體步驟：

2.1 列表：分成兩組，一組為滿足拔長條件，另一組為不滿足拔長條件，結果見表1。

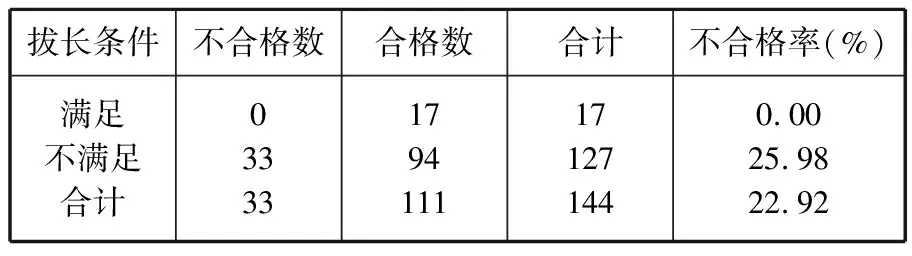
表1 滿足與不滿足拔長條件的兩組不合格狀態比較Table 1 Comparison of two unqualified state which meet and not meet the stretching condition

注：滿足拔長條件組的數目(分母)只有17，樣本量較小，但尚在范圍之內。

2.2 建立假設和確立顯著性水平：假設滿足拔長條件組與不滿足拔長條件組的探傷不合格率相等，均等于22.92%，顯著性水準為α=0.05。

2.3 計算理論頻數：根據以上假設，理論上不合格占33/144，合格占111/144。則滿足拔長條件組的不合格理論頻數=17×33/144=3.90，合格理論頻數=17×111/144=13.10。同樣，不滿足拔長條件組的不合格理論頻數=127×33/144=29.10，合格理論頻數=127×111/144=97.90。計算結果列入表2。

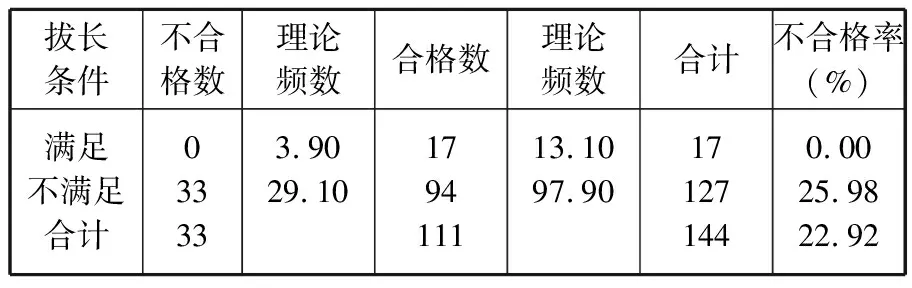
表2 滿足與不滿足拔長條件的兩組理論頻數四格表Table 2 Two set theoretical frequency of meeting or not the stretching condition

2.4 計算X2值：計算公式為

X2=∑(A-T)2/T

(1)

式中，A為實際頻數，T為理論頻數。

將表2中數據代入公式(1)得

X2=(0-3.9)2/3.9+(17-13.1)2/13.1+(33-29.1)2/29.1+(94-97.9)2/97.9=5.73

2.5 定自由度：公式為

n=(行數-1)(列數-1)

(2)

由于四格表是2行2列，故n=(2-1)(2-1)=1

2.6 確定P值: 查X2表[5]知，對于X2值為3.84，相應的P=0.05，對于X2值為5.02，相應的P=0.025，對于X2值為6.63，相應的P=0.01。所以，同一自由度下，X2值越大，P值就越小。本例的X2值為5.73，故0.05≥P>0.01，相差顯著。

2.7 推論結論：按α=0.05水準，拒絕假設檢驗，故認為兩組不合格率有差別。這說明，鍛壓拔長條件對大鍛件探傷有顯著影響，滿足拔長條件的工藝能提高超聲波探傷的合格率。

3 討論與推論

以上給出了大鍛件熱工藝小樣本統計學方法應用的理論和一個具體的應用示例，對在大鍛件領域開創科學統計學研究和應用具有一定重要意義。

值得注意的是，原始統計文獻中所給出的是多年前的數據，也沒有說明是否滿足煉鋼真空處理的條件。雖然目前上海重型機器廠的大鍛件所用鋼錠的冶煉已經全部實現了雙真空處理，而當時所統計的鍛件用鋼錠，并不是完全實現真空處理。為此，根據同質與異質的觀點，有理由懷疑樣本可能不是來自一個總體，而是來自規律不同的兩個總體。為此，需要進一步的研究確認。

在前述統計實例發生的同一時期還有一個專門針對管板的研究[6]，提供的數據見表3。

表3 管板采用與未采用真空處理的兩組理論頻數表Table 3 Two set theoretical frequency of tubeplate with or without vacuum pouring

用前面同樣的方法對表3進行計算，可得X2值為1.66。查表結果表明，P>0.05，認為兩組不合格率沒有顯著差別，即真空處理對探傷合格與否的影響不顯著。

以上似乎解決了問題，但我們還發現了一個問題。當對管板數據分析滿足與不滿足拔長條件對探傷結果的影響時，有表4的數據。

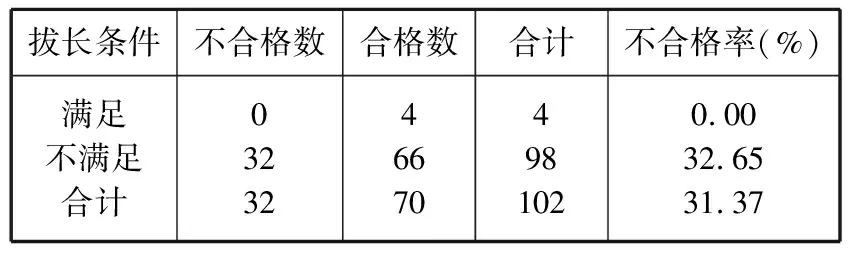
表4 管板滿足與不滿足拔長條件對探傷結果的影響Table 4 The influence of meeting or not the stretching condition on flaw detection result of tubeplate

值得注意的是，滿足拔長條件組的數目(分母)只有4，根據前面關于最小樣本量的觀點，表4的樣本量過小，它是隨機統計的數據，不是專門精密設計實驗、精選實驗對象、嚴格控制實驗條件的結果，因故而放棄對它的統計分析。

根據本文初步分析結果，得出結論如下：

拔長條件對某一時期內鍛件的探傷合格率的影響顯著；而真空處理對管板類鍛件的探傷合格率的影響不顯著；由于樣本量過小，拔長條件對管板類鍛件的探傷合格率的影響有待進一步研究。

4 結束語

本文給出示例之重點不僅僅是該示例本身的結論和推論，而是結合實際給出一種新的大鍛件工藝研究和驗證方法。本文重要的價值是在大鍛件生產領域開創統計學應用的方法。

對于本文所介紹的示例和該示例所要研究的問題，只要根據本文的方法，擴大統計范圍，就可以設計出新的研究課題，從而更加全面準確地研究本企業拔長條件與超聲波探傷的合格率的關系。類似的研究方法在醫學的臨床研究課題上非常成熟與普遍。

當前，我們的冶煉技術有了很大發展，探傷標準也更加嚴格。為了進一步提高大鍛件工藝水平和質量控制水平，我們完全有必要展開新的統計學科研課題的設計和研究。本文正是為這種需要而提供了基本方法。

[1] 朱延果.潔凈鋼技術.中國國際自由鍛會議2010，成都，2010.北京：中國鍛壓協會，2010.

[2] 聶微編著.2002版ISO TS16949實施指南.1版.廣州：廣東經濟出版社，2003：134-138.

[3] 齊作玉.大鍛件鍛壓工藝參數化的研究.大型鑄鍛件.2010(1)：9-29.

[4] 齊作玉，胡人龍，蘇良豐.宏觀控制鍛造法.大型鑄鍛件，1990(3)：23-65.

[5] 趙耐青，等編著.臨床醫學研究設計和數據分析.1版.上海:復旦大學出版社，2005：133-133.

[6] 齊作玉.管板鍛件的質量改進.鋼鐵.1990(12)：81-83.