復雜曲面CNC加工技術的曲面包絡逼近原理*

周凱紅 譚湘夫

(①桂林航天工業高等專科學校機械工程系，廣西桂林 541004;②湖南理工學院機械工程學院，湖南岳陽 414000)

飛行器機身、機翼覆蓋件和推進器葉片等重要零部件都是由空氣動力學原理設計的復雜曲面結構。其數控制造技術一直是飛行器制造技術的重要內容［1］。復雜曲面的現代數控制造技術是通過復雜曲面的NURBS離散數據驅動球面刀具相對工件運動實現的。盡管以NURBS法描述復雜曲面的優點已為眾多相關研究所證實［2］，但是，由其驅動球面刀具完成復雜曲面的數控加工卻存在難以接受的缺點:低效率的材料“點”去除加工、高成本的球面刀具。

在多軸聯動數控技術出現以前，由于機床加工運動功能的局限性，在刀具相對工件的包絡運動中，刀具包絡面的特征線(刀刃線)相對刀具是靜止的(如仿形法)或沿刀具曲面平動(如范成法)，這些都無法充分利用刀具曲面上豐富的曲線去擬合加工目標曲面。在多軸聯動數控技術出現以后，由于對直接面向數控加工的曲面逼近理論研究上的不足，通常以NURBS離散數據驅動球面刀具以“點”去除方式來逼近復雜曲面，這實際上是將刀具曲面包絡面的特征線(刀刃線)的長度視為零，沒有充分利用刀具曲面上的曲線去擬合加工目標曲面。

本文基于微分幾何中的曲面活動標架理論提出了一種面向數控加工的曲面逼近理論(包絡逼近原理):它以簡單(刀具)曲面(如平面、圓柱面、圓錐面和各種螺旋面等)上的定向曲面片(包絡面特征線上的微分流形)為基函數，以刀具相對工件的相對運動(變換)形成的包絡面按指定的約束條件和精度逼近加工目標曲面，從而獲得刀具相對工件的相對運動方程(變換矩陣)。基于包絡逼近原理的曲面數控制造技術，其刀具形狀是按加工目標曲面設計的簡單曲面，其材料去除方式是“線”去除，因而其加工效率較現行球面刀具“點”去除加工方法高，刀具成本低。曲面包絡逼近原理也是各種金屬切削加工方法的幾何學基礎。本文將簡述曲面包絡逼近的數學原理，并通過一個點嚙合齒面的曲面構造論證包絡逼近原理的應用方法。

1 曲面的包絡逼近原理［3］

活動標架的概念起源于研究剛體運動。Darboux［4］等以空間曲線的Frenet標架沿曲線的運動來研究空間曲線的微分結構。E.Cartan［5］將活動標架引入空間曲面的研究，又將其從運動群推廣到任意線性變換群，并引進外微分形式，形成研究曲面微分結構的新方法。這一新方法的特點是將曲面微分特性與標架沿曲面的運動聯系起來，特別適合描述和控制刀具展成復雜曲面的相對運動。曲面包絡逼近原理就是通過刀具曲面與目標曲面活動標架的相對運動關系來描述刀具相對工件的運動，并通過曲面逼近條件來確定刀具與工件的相對運動。

1.1 曲面活動標架下曲面與其包絡面的相對運動

如圖1，曲面Σ(t)通過相對于坐標系Sp［O(p);x(p)y(p)z(p)］的運動Ψ包絡出曲面Σ(g)。設Lp是曲面Σ(g)上的一條曲線，Lt是曲面Σ(t)上的一條曲線，Lp與Lt對于運動Ψ相互共軛。Lg是形成包絡曲面Σ(g)的特征線。因此，在運動的任意時刻，曲面Σ(t)與Σ(g)相切于Lg，而Lg總與Lt和Lp三線交于點M。故在點M對于曲面 Σ(t)與 Σ(g)分別有活動標架 Sft［M;αtvtnt］和 Sfp［M;αpvpnp］。其中，αi(i=t，p)是曲線 Li在點 M 的單位切矢，ni是曲面Σ(i)在點M的單位法矢，vi=ni×αi。另有一曲面Σ(p)與曲面Σ(g)固結且沿曲線Lp與曲面Σ(g)具有二階切觸，圖1中未標出。即曲面Σ(g)和曲面Σ(p)沿曲線Lp二階及二階以下參數均相等。曲面Σ(t)相對曲面Σ(g)的角速度為

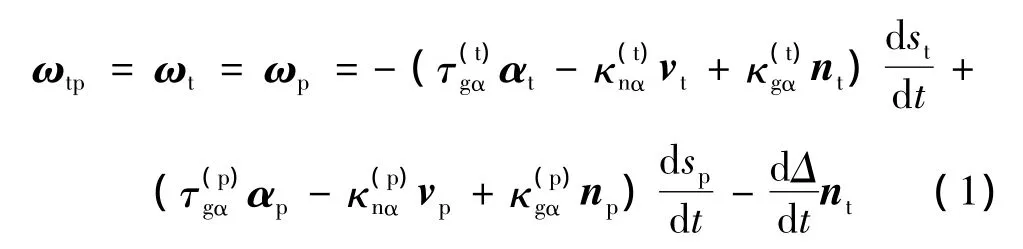
在M點曲面Σ(t)相對曲面Σ(g)的速度為

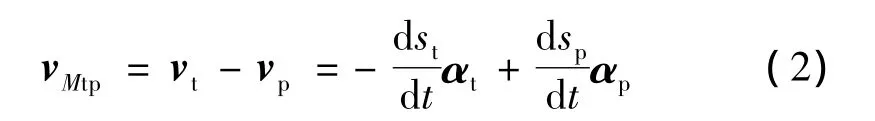
因此，在任意點點曲面Σ(t)相對曲面Σ(g)的速度為

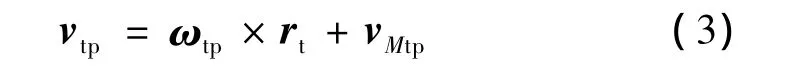
這里:dsp/dt=|driM/dt|(i=t，p)是點M在曲面Σ(i)上沿曲線Li運動的速率;riM是曲線Li上嚙合點M的位置矢量;τ(i)gα、κ(i)nα分別是曲面 Σ(i)在點 M 沿 αi方向的短程撓率和法曲率，κ(i)gα是曲面 Σ(i)在點M 沿 αi方向的短程曲率;rt是曲面Σ(t)任意一點的位置矢量。

于是，曲面Σ(t)的包絡運動Ψ被表示為曲面Σ(t)和Σ(g)及其各自曲面上的曲線的微分幾何(活動標架運動)參數及兩曲面活動標架的相對位置參數的函數。實際上，運動Ψ也代表一種從曲面Σ(t)到曲面Σ(g)的運動變換。如果曲面Σ(t)是一種曲面結構比較簡單的刀具曲面(如平面、圓柱面、圓錐面和各種螺旋面等)，那么，通過控制這種變換就可能包絡出結構復雜的曲面Σ(g)使其以最小的誤差逼近一個加工目標曲面。這就是包絡逼近原理。

1.2 從曲面Σ(t)到曲面Σ(g)的運動變換及曲面Σ(g)的方程

為了實現上述最小誤差逼近，有必要寫出包絡運動Ψ的變換矩陣和曲面Σ(g)的數學表達式，以便建立這種最優曲面逼近模型。

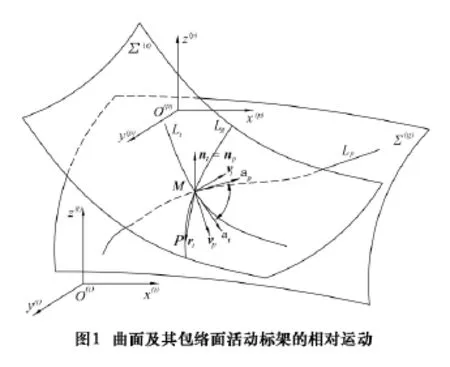
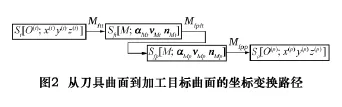
由圖1可知，從曲面Σ(t)到曲面Σ(g)的坐標變換路徑如圖2所示。因此，從曲面Σ(t)到曲面Σ(g)的變換矩陣為

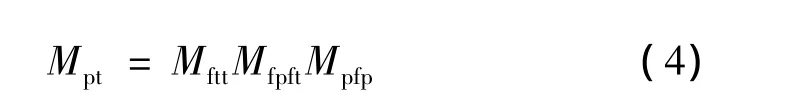
其中:

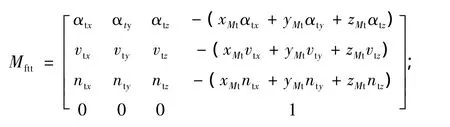
曲面Σ(t)的包絡面Σ(g)的方程

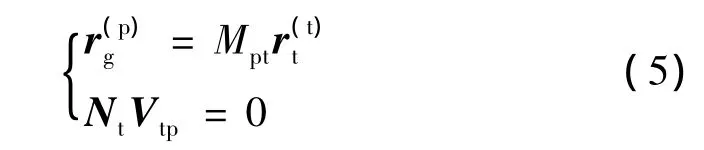
由式(4)、(5)的分析可知，式(5)所確定的包絡面Σ(g)的方程是由曲面Σ(t)、曲線Lp與Lt的相應參數及Δ來描述的。如果我們把包絡面Σ(g)上的曲線Lp作為Σ(g)逼近目標曲面Σ(p)的約束條件，則通過控制Δ函數可以得到適當的包絡運動Ψ，使包絡面Σ(g)在曲線Lp以外的區域逼近Σ(p)

1.3 曲面Σ(t)的包絡面Σ(g)逼近目標曲面Σ(p)

如圖3，包絡面Σ(g)以曲線Lp為約束條件逼近曲面 Σ(p)，即 Σ(g)可以與 Σ(p)相交(或相切)于 Lp。Lg是組成Σ(p)的過Lp上任意點M的包絡特征線，點和是Lg的兩個端點，Qg是Lg上這兩個端點之間的任意一點。Qg與它在目標曲面Σ(p)上的對應點Qp由圖3所示來確定。故曲面Σ(g)在其任意點與目標曲面Σ(p)的偏差δ表示為

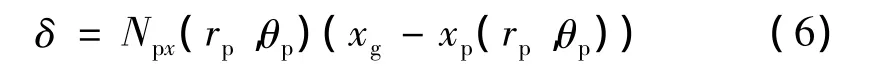
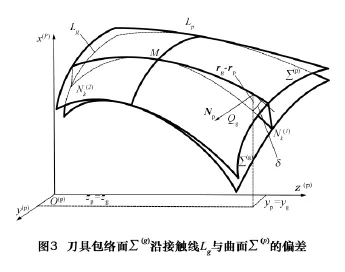
沿Lg各點以兩端點N(1)k和N(2)k所對應的偏差和最大，只有同時控制和，才能保證曲面Σ(g)逼近目標曲面Σ(p)的精度。故包絡面Σ(g)逼近目標曲面Σ(p)的最優模型:

目標函數為

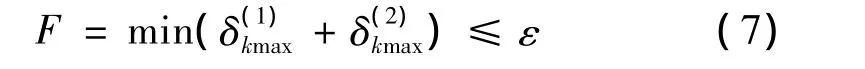
約束條件為

約束條件式(8)保證曲面Σ(g)從目標曲面Σ(p)的外側逼近目標曲面Σ(p)。式(7)中的ε是預定的曲面逼近的誤差。當+的最小值不能滿足式(7)時，一般有兩種方法進行改進:(1)根據目標曲面Σ(p)的形狀重新選擇或設計刀具曲面Σ(t)。(2)縮小包絡逼近的區域，即減小端點N(1)k和N(2)k離開點M的距離。通過求解由式(7)和(8)構成的優化模型可以確定Δ函數，從而由式(3)和(4)得到刀具相對工件的運動方程和變換矩陣。將這個運動方程和變換矩陣在多軸聯動數控機床上等效實現，就可在數控機床上完成用刀具Σ(t)對目標曲面Σ(p)的“線”去除加工。

2 曲面的包絡逼近原理在點嚙合齒面展成上的應用實例

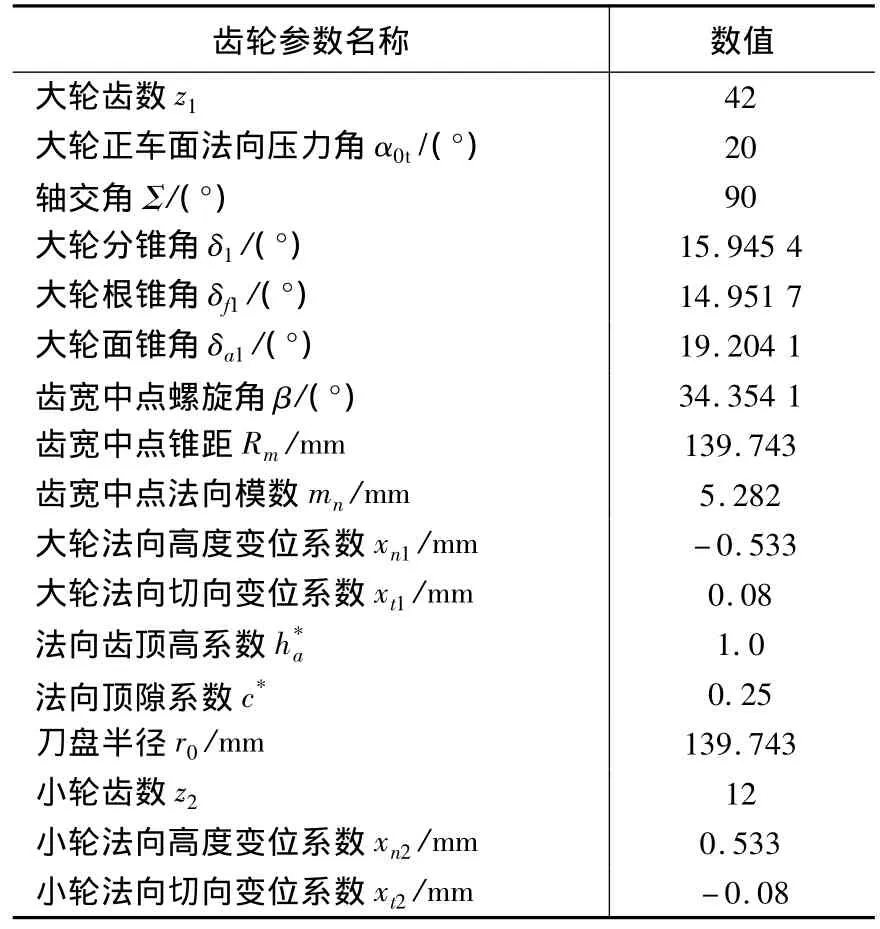
表1 齒輪副主要幾何參數表

弧齒錐齒輪副是一種航空領域常用的高速重載動力傳動的點嚙合齒面傳動。傳動過程中嚙合點在齒面上的軌跡就是接觸跡線。在這種齒輪副中，大輪齒面一般是由成形法加工得到的圓錐面，而小輪齒面與大輪齒面配對嚙合必須滿足多種嚙合特性，一般是復雜曲面。但展成這種小輪齒面的刀具曲面仍是簡單的圓錐面。本例依據曲面的包絡逼近原理，通過刀具圓錐面Σ(t)運動產生的包絡面 Σ(g)逼近這種復雜曲面Σ(p)。這里，曲面逼近的約束條件就是包絡面Σ(g)沿齒面接觸跡線Lp與Σ(p)具有二階切觸。

表1是所研究齒輪副的安裝傳動的主要幾何尺寸。表2是齒面接觸跡線Lp的離散點坐標及其對應的主曲率。小輪的理論齒面Σ(p)就是大輪齒面在上述齒輪副安裝傳動條件下的包絡面。

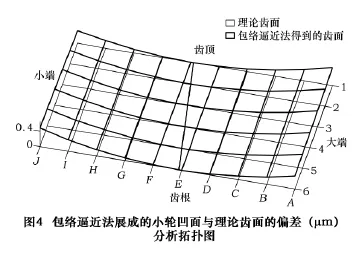
圖4是包絡逼近法展成的小輪凹面與理論齒面凹面的偏差分析拓撲圖。圖中數據表明實際加工得到的齒面與理論齒面沿接觸跡線Lp相切，且在遠離接觸跡線的齒面邊緣，與理論齒面的最大偏差只有0.45 μm，這表明只要根據加工目標曲面的形狀設計適當的刀具曲面，按包絡逼近法展成的曲面可以在一定曲面范圍內以很小的誤差逼近目標曲面。圖5是按包絡逼近法在UG中構造的小輪齒槽三維實體。

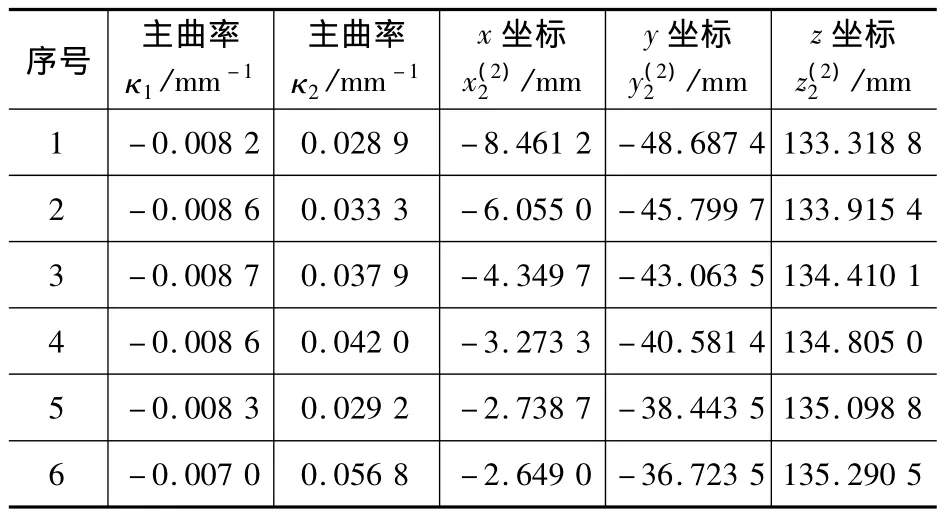
表2 齒面接觸跡線上部分點的主曲率及坐標

3 結語

本文論述的曲面包絡逼近理論是以材料的“線”去除方式加工復雜曲面的CNC制造技術的幾何學基礎，是直接面向數控加工的曲面逼近理論。由于該方法以“線”去除方式加工復雜曲面，因此，比以往的材料“點”去除加工方法加工效率要高。實例計算表明:只要根據加工目標曲面的結構設計刀具曲面，由包絡逼近原理加工目標曲面就能達到足夠的加工精度要求。

［1］張耀.航空科學技術的發展［M］.北京:航空工業出版社，2007:129－133.

［2］朱新雄，等.自由曲線曲面造型技術［M］.北京:科學出版社，2003:138－168.

［3］周凱紅.基于預定嚙合特性的螺旋錐齒輪點嚙合齒面設計及CNC制造技術研究［D］長沙:中南大學，2009.

［4］Pogorelov A V，Differential geometry［M］.Netherlands:Noordhoff，Groningen，1958:38－41.

［5］O’Nell B.Elementary differential geometry［M］.New York:Academic Press，1966:52 －56.