鋼錠鍛造用套筒套的設計與計算

曹志遠 季 雪 程幸葉 牛廣斌

(天津重型裝備工程研究有限公司，天津300457)

套筒是大型鋼錠自由鍛造時不可缺少的鍛造附具，其與鋼錠的鉗口配合在天車配備的翻鋼機的帶動下來實現鋼錠的移動和旋轉。隨著工業的發展和鍛壓水平的提高，水壓機鍛造鋼錠的最大噸位也由200 t級向更大噸位邁進，即使新型水壓機配備了大型操作機也不能完全替代套筒這種傳統的鍛造附具，所以有必要設計更大噸位級的套筒。

1 按照懸臂梁假設推導公式

鋼錠尺寸示意圖見圖1，錠身重量與重心的計算公式如下：

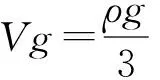
假設鋼錠鉗口與翻鋼機套筒緊密接觸，可認為鋼錠是一個懸臂梁，如圖2所示。

外載荷：M=Gh2，Q=G

(1)彎曲正應力

最大彎曲正應力：

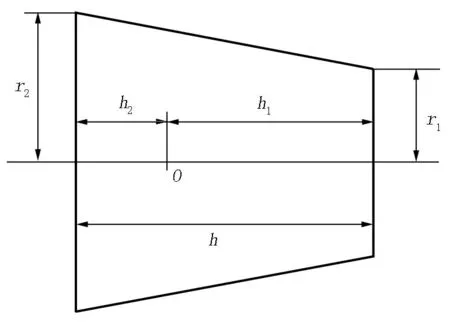
圖1

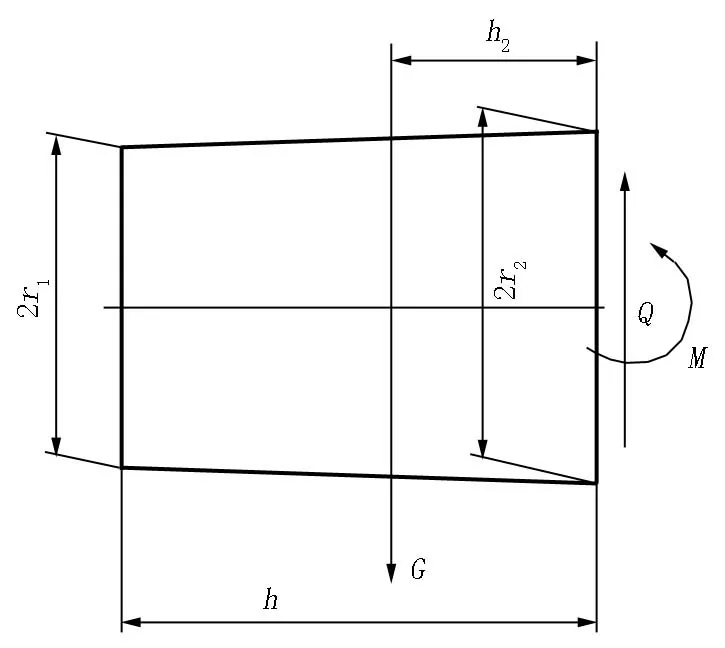
圖2

位置y的彎曲正應力：

(2)彎曲剪應力

最大彎曲剪應力：

位置y的彎曲剪應力：

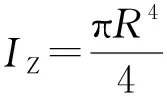
(3)兩種強度考慮

彎曲強度條件：σmax≤σs=9.69 MPa，

剪切強度條件：τmax≤τ(s)=5.59 MPa

(4)Mises屈服準則

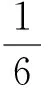
σx=σ，τxy=τ，σy=σz=τyz=τzx=0

F(y)=σ(y)2+3τ(y)2

F(y)是一個開口朝上的拋物線，其最大值位于兩端，即y=0，和y=R

記錄兩種診斷方式的檢查結果，并與最終手術治療結果進行對比，統計兩種方式的誤診、漏診人數，以此計算各診斷方式的診斷準確率；記錄兩種診斷方式檢查得出的突出征象，并與最終手術治療結果進行對比，統計具體病因診斷的準確率。

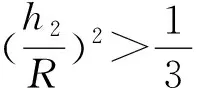
這個結果與前面的結論一致。為了有更大的保險系數，我們假設τs=σs/2，判斷準則為：

2 按照杠桿式假設推導公式

假設考慮鋼錠鉗口直徑略小于套筒直徑，則二者接觸成為杠桿式，見圖3。在A、B二處為線接觸，B處平衡力矩為F1，這時支點A處承受的集中力為F，則有：

圖3

應用剪應力強度理論，按此計算最小鉗口直徑R2：

顯然這個數值大于彎曲正應力強度理論計算出的數值。

這種杠桿式推導公式更接近于生產實際，且增大l有利于減小鉗口直徑R2的尺寸。

3 結論

(1)鉗口與套筒緊密接觸，彎曲正應力引起的抗拉破壞最大，鉗口設計的最小直徑應以此為準；

(2)鉗口與套筒非緊密接觸，鋼錠鉗口直徑略小于套筒直徑，剪切應力引起的破壞最大，鉗口設計的最小直徑應以此為準，同時可以考慮增大鉗口長度可適當彌補鉗口直徑小的不足。

(3)套筒直徑應以鉗口與套筒非緊密接觸方式的計算方法為準，非緊密接觸更接近生產實際。